Оглавление:
Ранг матрицы
Рангом матрицы называется наибольший из порядков ее миноров, отличных от нуля. Если все миноры матрицы равны нулю, то ранг матрицы считается равным нулю.
Ранг матрицы 
будем обозначать 
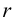или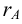 
.
Очевидно, что если в матрице имеется отличный от нуля минор порядка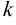 
, а все миноры порядка 
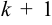либо равны нулю, либо не существуют, то 
.
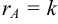Если ранг квадратной матрицы порядка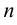 
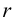равен , то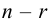 
называют дефектом матрицы . Если — невырожденная (
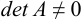), то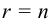 
и дефект матрицы равен нулю.
Элементарными преобразованиями матрицы назовем следующие:
1) умножение некоторого ряда матрицы на число, отличное от нуля;
2) прибавление к одному ряду матрицы другого, параллельного ему ряда, умноженного на произвольное число;
3) перестановку местами двух параллельных рядов матрицы.
Если матрица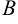 
получена из матрицы некоторым элементарным преобразованием, а матрица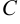 
, в свою очередь, получена из матрицы 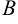также элементарным преобразованием, то говорят, что матрица 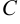получена из матрицы последовательным применением этих преобразований.
Если матрица 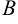получена из матрицы путем элементарного преобразования, то будем писать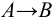 
.
Теорема. Ранг матрицы, полученной из данной элементарными преобразованиями, равен рангу исходной матрицы.
Минор порядка 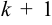, содержащий в себе минор 
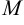порядка 
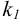, называется окаймляющим минор .
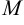Метод окаймляющих миноров основан на том, что ранг данной матрицы равен порядку такого минора этой матрицы, который отличен от нуля, а все окаймляющие его миноры равны нулю.
Задача №6.
Найти ранг матрицы
Решение:
Так как среди миноров второго порядка данной матрицы есть отличные от нуля, например, минор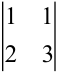 
, а все миноры третьего порядка равны нулю (в этих минорах имеются пропорциональные строки), то 
.
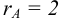Задача №7.
Найти ранг матрицы
Решение:
Приведем матрицу к трапециевидной форме. Прибавив ко второй строке первую, умноженную на -2, к третьей — первую, умноженную на -3, к четвертой — первую, умноженную на -1, получим
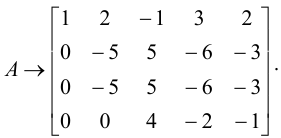
Прибавив к третьей строке вторую, умноженную на -1, и поменяв местами в полученной матрице третью и четвертую строки, имеем
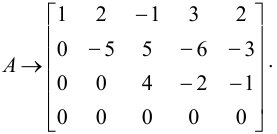
Эта матрица является трапециевидной ранга 3. Следовательно,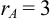 
.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
| Определители задачи с решением |
| Обратная матрица с решением задачи |
| Матричное решение системы линейных уравнений задачи с решением |
| Решение произвольных систем матриц задача с решением |
