Ранг матрицы

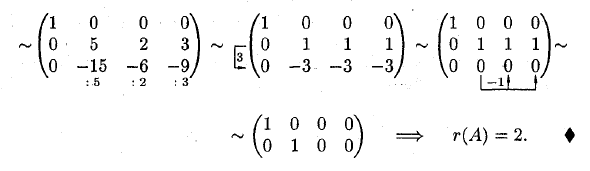
Ранг матрицы

• Матричный ранг Рассмотрим матрицу A размером m × n. / \ dn «ai2 \ ai3 … ajn \ a23 ••• a-2n A = ft3i «32« s … Q> 3n » \ Oml Qm2 Gm3 ••• amn Среди них выберите k строк и k столбцов (k.Min (m; n)). Создайте определитель k-го порядка из элементов на пересечении выбранной строки и столбца. Все эти детерминанты называются минорами этой матрицы. В матрице .

4 пунктирная линия — второй минор. (Обратите внимание, что такие несовершеннолетние могут сочинять. С * шт. C * = ^ y — количество комбинаций из n элементов. Согласно к) Максимальный младший порядок конкретной матрицы, отличной от нуля, называется рангом матрицы. Это указано как g, g (A) или звонил А. Очевидно, что 0 ^ r ^ min (m; n), где min (m; n) является меньшим из m и 71.

Несовершеннолетний, порядок которого определяет ранг матрицы, называется базисом. Людмила Фирмаль

Матрица может содержать несколько основных миноров. Пример:♦ Все третичные несовершеннолетние равны нулю. Есть второй несовершеннолетний, 3 б = -15Φ0. Следовательно, r (A) = 2. 1-3 Ненулевая Младший находится на пересечении строк 2 и 3 и столбцов 1 и 3. ♦ Обратите внимание на свойство ранга матрицы. 1. Транспонирование матрицы не меняет ее ранг. 2. Удаление нулевых строк из матрицы не меняет ранг матрицы.

При базовом преобразовании матрицы ранг матрицы не изменяется. • Поменяйте местами два параллельных столбца матрицы. • Умножьте каждый элемент строки матрицы на ненулевое число. • Для каждого элемента в строке матрицы добавьте соответствующий элемент в параллельном ряду, умноженный на тот же номер. Две матрицы A-B называются эквивалентными, если одна получена из другой с помощью базового преобразования. А до Б записываются.

• Используя базовое преобразование, вы можете уменьшить произвольную матрицу до матрицы, которая имеет несколько единиц в первой строке главной диагонали и все остальные элементы равны нулю. / 1 0 0 0 \ 0 10 0 0 0 10 \ 0 0 0 0, Ранг канонической матрицы равен количеству единиц на главной диагонали. Это основа для расчета ранга матрицы. Пример: / 2 3 1 2 \ A = 0 2 -1 1, г (A) =? \ 4 0 5 1 / ♦ Выполнение базового преобразования -2 Такая матрица называется стандартом.

Например,0 1 • 3 0 1 3 1 0 0 0 ‘ 0 111 0 0 0 0 I-It g 0 о 0 \ 1 час G (A) = 2. Людмила Фирмаль

Смотрите также:

Предмет высшая математика

Действия над матрицами	Системы линейных уравнений (основные понятия)
Обратная матрица	Решение невырожденных линейных систем. формулы крамера