Оглавление:
Радикальный признак Коши
Иногда удобно пользоваться радикальным признаком Коши для исследования сходимости знакоположительного ряда. Этот признак во многом схож с признаком Даламбера, о чем говорят его формулировка и доказательство.
Теорема 60.4. Пусть дан ряд (59.1) с положительными членами и существует конечный или бесконечный предел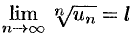 
. Тогда ряд сходится при 
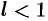и расходится при 
.
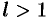Как и для признака Даламбера, в случае, когда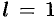 
, вопрос о сходимости ряда остается открытым. Доказательство теоремы аналогично доказательству признака Даламбера. Поэтому опустим его.
Пример №60.6.
Исследовать на сходимость ряд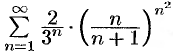 
.
Решение:
Так как
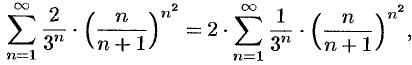
то применим радикальный признак Коши к ряду
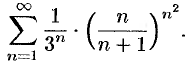
Вычисляем
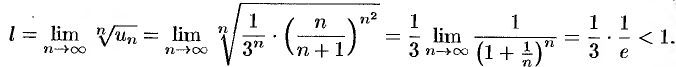
Ряд 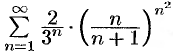сходится, а значит, сходится и исходный ряд, согласно свойству 1 числовых рядов.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Достаточные признаки сходимости знакопостоянных рядов |
| Признак Даламбера |
| Интегральный признак Коши |
| Знакочередующиеся ряды. Признак Лейбница |
