Работа внутренних сил неизменяемой системы
Под неизменяемой системой материальных точек понимается такая система, расстояния между точками которой при движении системы не изменяются. Такой системой является всякое абсолютно твердое тело. Пусть
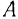 и
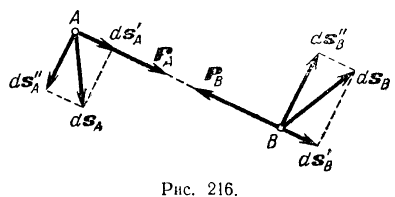
и 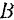 — две точки какой-либо неизменяемой системы (рис. 216).
— две точки какой-либо неизменяемой системы (рис. 216). 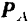 и
и 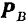 — равные по модулю и противоположные по направлению силы взаимодействия между этими точками. Допустим, что при движении системы за промежуток времени
— равные по модулю и противоположные по направлению силы взаимодействия между этими точками. Допустим, что при движении системы за промежуток времени 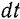 точки
точки 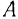 и
и 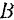 получают элементарные перемещения
получают элементарные перемещения 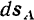 и
и 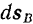 . Разложим каждое из этих перемещений на составляющие: одно, направленное по линии
. Разложим каждое из этих перемещений на составляющие: одно, направленное по линии 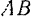 действия сил, и второе, перпендикулярное к этой линии. На перемещениях
действия сил, и второе, перпендикулярное к этой линии. На перемещениях 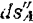 и
и 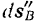 , перпендикулярных к линиям действия сил, силы работы не производят. Так как расстояние между точками
, перпендикулярных к линиям действия сил, силы работы не производят. Так как расстояние между точками 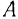 и
и 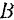 неизменяемой системы при ее движении изменяться не может, то перемещения
неизменяемой системы при ее движении изменяться не может, то перемещения 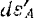 и
и 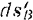 должны быть равны и направлены в одну сторону. Отсюда следует, что
должны быть равны и направлены в одну сторону. Отсюда следует, что
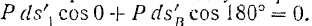
Данный результат, очевидно, можно распространить и на всю неизменяемую систему точек, рассматривая их попарно.
Таким образом, сумма работ внутренних сил неизменяемой системы при всяком ее перемещении равна нулю.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Работа силы тяжести с примером решения |
| Работа силы упругости |
| Мощность силы с примером решения |
| Работа и мощность силы, приложенной к вращающемуся телу с примером решения |

