Работа силы упругости
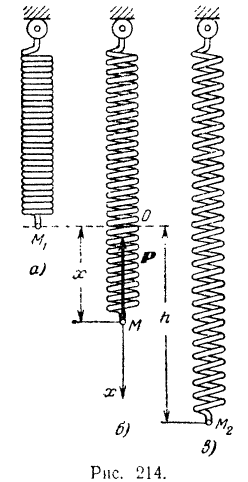
По закону Гука сила 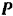 упругости растягиваемой пружины (рис. 214,о) до известных пределов прямо пропорциональна величине ее удлинения. Обозначая удаление пружины через
упругости растягиваемой пружины (рис. 214,о) до известных пределов прямо пропорциональна величине ее удлинения. Обозначая удаление пружины через 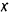 (рис. 214, 0) будем иметь:
(рис. 214, 0) будем иметь:
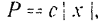
где 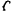 — постоянный для данной пружины коэффициент пропорциональности, называемый коэффициентом жесткости пружины.
— постоянный для данной пружины коэффициент пропорциональности, называемый коэффициентом жесткости пружины.
Вычислим работу переменной силы 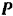 при удлинении пружины на некоторую величину
при удлинении пружины на некоторую величину 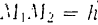 (рис. 214, в). Примем прямолинейную траекторию точки
(рис. 214, в). Примем прямолинейную траекторию точки 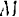 за ось
за ось 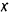 , направив эту ось вертикально вниз (рис. 214.6). За начало координат возьмем точку
, направив эту ось вертикально вниз (рис. 214.6). За начало координат возьмем точку 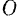 , соответствующую положению точки
, соответствующую положению точки 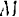 при недеформированном состоянии пружины.
при недеформированном состоянии пружины.
Проекции силы упругости 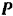 па координатные оси:
па координатные оси:
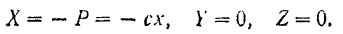
Подставляя эти значения в выражение (189) элементарной работы, получим
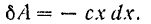
Работа же силы 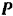 на конечном перемещении
на конечном перемещении 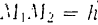 ее точки приложения будет равна
ее точки приложения будет равна
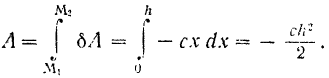
По этой формуле определяется работа не силы упругости растягиваемой пружины, но и силы упругости, возникающей при растяжении любого прямолинейного бруса, изгибе балки и т.д.— но всех случаях, когда существует пропорциональность между силой и деформацией, т. е. когда имеет место закон Гука.
Работа силы 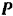 упругости тела, выражаемой законом Гука, равна половине произведения коэффициента жесткости на квадрат перемещения ее точки приложения, отсчитанного от положения этой точки при недеформированном состоянии тела:
упругости тела, выражаемой законом Гука, равна половине произведения коэффициента жесткости на квадрат перемещения ее точки приложения, отсчитанного от положения этой точки при недеформированном состоянии тела:
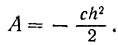
Знак минус в формуле (196) показывает, что работа силы упругости, как и всякой силы сопротивления, отрицательна. Так как внешняя растягивающая сила равна но .модулю упругой силе и направлена противоположно, то работа 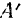 внешней силы по модулю равна
внешней силы по модулю равна 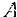 не положительна:
не положительна:
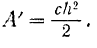
Такова работа, которою нужно затратить, для того чтобы удлинить пружину на величину 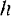 .
.
Зависимость между модулем упругой силы  и перемещением
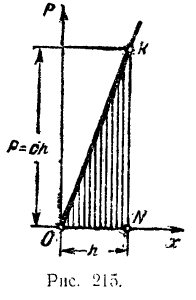
и перемещением 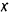 точки ее приложения графически выражается, очевидно, прямой линией (рис. 215). В соответствии со сказанным ранее работа этой силы на некотором пути
точки ее приложения графически выражается, очевидно, прямой линией (рис. 215). В соответствии со сказанным ранее работа этой силы на некотором пути 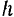 выразится, в соответствующем масштабе, площадью
выразится, в соответствующем масштабе, площадью 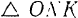 . Таким образом, мы вновь приходим к установленному выше численному значению работы другой силы:
. Таким образом, мы вновь приходим к установленному выше численному значению работы другой силы:
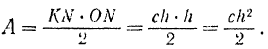
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Теорема о работе равнодействующей |
| Работа силы тяжести с примером решения |
| Работа внутренних сил неизменяемой системы |
| Мощность силы с примером решения |

