Работа силы на перемещении. Силовая функция
Понятие работы силы на элементарном перемещении является одним из важнейших в механике. Пусть материальная точка, находящаяся под действием силы 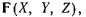 совершает некоторое элементарное перемещение из положения
совершает некоторое элементарное перемещение из положения 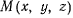 в положение
в положение 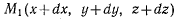 и вектор элементарного перемещения точки
и вектор элементарного перемещения точки 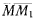 имеет проекции на неподвижные оси
имеет проекции на неподвижные оси 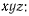
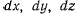 (рис. 117). Вне зависимости от того, будет или нет сила F действовать на точку на всем перемещении, работой силы F на элементарном перемещении
(рис. 117). Вне зависимости от того, будет или нет сила F действовать на точку на всем перемещении, работой силы F на элементарном перемещении 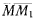 будем называть скалярное произведение силы F и перемещения
будем называть скалярное произведение силы F и перемещения 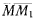
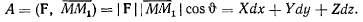
Это формальное определение теряет смысл, если не говорится о силе или о перемещении. Рассмотрим некоторые примеры.
В определении работы не возникает никаких сомнений, если сила действует на материальную точку на всем перемещении.
Предположим, что тяжелый цилиндр находится на гладкой горизонтальной плоскости (рис. 118). Тогда со стороны плоскости на цилиндр будет действовать сила реакции R, направленная перпендикулярно к плоскости. Если сообщить цилиндру бесконечно малое перемещение 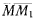 и при котором он покидает плоскость, то работа силы R на этом перемещении, по опреде-
и при котором он покидает плоскость, то работа силы R на этом перемещении, по опреде-
лению, будет отлична от нуля, хотя сила R и перестает действовать на цилиндр, как только последний начнет перемещаться.
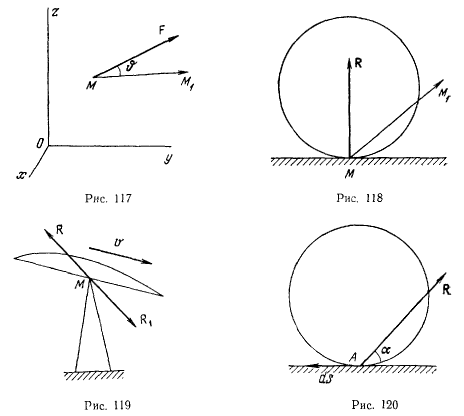
Рассмотрим перемещение шероховатой пластинки по острию (рис. 119). На точку М пластинки действует сила реакции R, которая совершает отличную от нуля работу на перемещении точки М пластинки, хоти сила R и не действует па точку М пластинки на всем ее перемещении. На острие со стороны пластинки действует сила 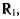 , равная по величине силе R, но направленная в противоположную сторону. Эта сила
, равная по величине силе R, но направленная в противоположную сторону. Эта сила 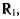 не совершает работы на перемещении точки М острия, так как острие остается неподвижным.
не совершает работы на перемещении точки М острия, так как острие остается неподвижным.
Цилиндр катится без скольжения по плоскости. Если плоскость шероховата, то на цилиндр со стороны плоскости в общем случае действует сила реакции R, направленная под некоторым углом и к плоскости (рис. 120). Работа силы R на перемещении точки А цилиндра равна нулю, а на перемещении 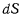 точки касания плоскости с цилиндром работа силы R отлична от нуля.
точки касания плоскости с цилиндром работа силы R отлична от нуля.
Если элементарные перемещения точки образуют целую линию L и сила действует на точку на всем ее перемещении ио линии, то можно говорить о работе силы на криволинейном пути материальной точки, определяя эту работу криволинейным интегралом
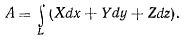
В общем случае эта работа зависит не только от силы, действующей на точку, но и от вида кривой, по которой перемещается точка. Если элементарная работа силы на бесконечно малом перемещении представляет собой полный дифференциал некоторой функции 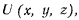 зависящей только от координат точки, т. е. имеет место равенство
зависящей только от координат точки, т. е. имеет место равенство
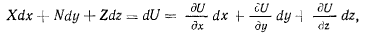
то силы, действующие на материальную точку, могут быть представлены частными производными от этой функции
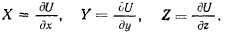
Функция U называется силовой функцией. Необходимые и достаточные условия существовании силовой функции можно представить в виде
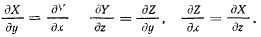
При выполнении этих условий работа силы на криволинейном участке пути будет зависеть лишь от начального и конечного положений точки. В самом деле
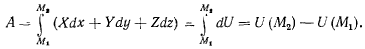
Силы, обладающие этим свойством, называются консервативными. Если силовая функция однозначна, то, как известно, интеграл по замкнутому контуру будет равен нулю. Для неоднозначных функций этот интеграл может быть и отличным от нуля. Поверхности, на которых силовая функция принимает постоянное значение
Чтобы выяснить, как расположены силы по отношению к поверхности уровня, рассмотрим систему прямоугольных осей 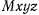 с началом в точке М поверхности уровня так, чтобы оси х и у были расположены в касательной плоскости к поверхности уровня. Ось z направим по нормали к поверхности в сторону увеличения функции
с началом в точке М поверхности уровня так, чтобы оси х и у были расположены в касательной плоскости к поверхности уровня. Ось z направим по нормали к поверхности в сторону увеличения функции 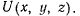 Тогда, представляя V как функцию координат х, у, z, в точке М будем иметь
Тогда, представляя V как функцию координат х, у, z, в точке М будем иметь
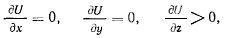
откуда
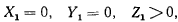
т. е. сила направлена ортогонально к поверхности уровня в сторону возрастания силовой функции.
Рассмотрим некоторые наиболее важные примеры сил, обладающих силовой функцией.
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Задача о равновесии при наличии трения |
| Сила тяжести и центр тяжести |
| Сила тяжести |
| Упругая сила |

