Работа переменной силы
Пусть материальная точка 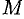 перемещается под действием силы
перемещается под действием силы 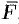 , направленной вдоль оси
, направленной вдоль оси 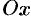 и имеющей переменную величину
и имеющей переменную величину 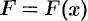 , где
, где 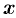 — абсцисса движущейся точки
— абсцисса движущейся точки 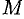 .
.
Найдем работу 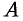 силы
силы 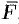 по перемещению точки
по перемещению точки 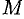 вдоль оси
вдоль оси 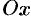 из точки
из точки 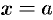 в точку
в точку 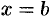 (
(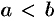 ). Для этого отрезок
). Для этого отрезок  точками
точками 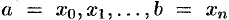
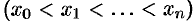 разобьем на
разобьем на  частичных отрезков
частичных отрезков 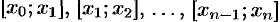 . Сила, действующая на отрезке
. Сила, действующая на отрезке 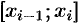 , меняется от точки к точке. Но если длина отрезка
, меняется от точки к точке. Но если длина отрезка 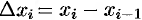 достаточно мала, то сила
достаточно мала, то сила 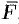 на этом отрезке изменяется незначительно. Ее можно приближенно считать постоянной и равной значению функции
на этом отрезке изменяется незначительно. Ее можно приближенно считать постоянной и равной значению функции 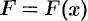 в произвольно выбранной точке
в произвольно выбранной точке 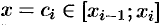 . Поэтому работа, совершенная этой силой на отрезке
. Поэтому работа, совершенная этой силой на отрезке 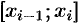 , равна произведению
, равна произведению 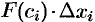 . (Как работа постоянной силы
. (Как работа постоянной силы 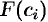 на участке
на участке 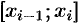 .)
.)
Приближенное значение работы 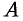 силы
силы 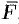 на всем отрезке
на всем отрезке  есть
есть
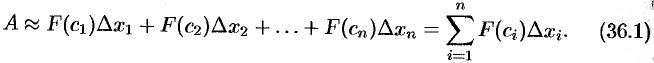
Это приближенное равенство тем точнее, чем меньше длина 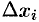 . Поэтому за точное значение работы
. Поэтому за точное значение работы 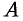 принимается предел суммы (36.1). при условии, что наибольшая длина
принимается предел суммы (36.1). при условии, что наибольшая длина 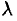 частичных отрезков стремится к нулю:
частичных отрезков стремится к нулю:
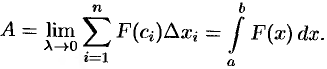
Итак, работа переменной силы 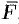 , величина которой есть непрерывная функция
, величина которой есть непрерывная функция 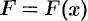 , действующей на отрезке
, действующей на отрезке  , равна определенному интегралу от величины
, равна определенному интегралу от величины 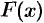 силы, взятому по отрезку
силы, взятому по отрезку  .
.
В этом состоит физический смысл определенного интеграла.
Аналогично можно показать, что путь 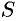 , пройденный точкой за промежуток времени от
, пройденный точкой за промежуток времени от 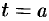 до
до 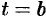 , равен определенному интегралу от скорости
, равен определенному интегралу от скорости 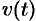 :
:
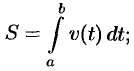
масса 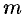 неоднородного стержня па отрезке
неоднородного стержня па отрезке  равна определенному интегралу от плотности
равна определенному интегралу от плотности 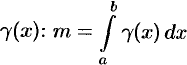 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Гиперболический параболоид |
| Конус второго порядка |
| Интегрирование четных и нечетных функций в симметричных пределах |
| Давление жидкости на вертикальную пластинку |

