Оглавление:
Работа и мощность силы, приложенной к вращающемуся телу
Пусть в некоторой точке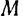 
твердого тела, вращающегося вокруг неподвижной оси 
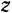(рис. 217), приложена сила 
.
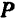Разложим эту силу на две взаимно перпендикулярные составляющие: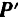 
, лежащую в плоскости 
. перпендикулярной к оси вращения тела, и 
, параллельную оси .
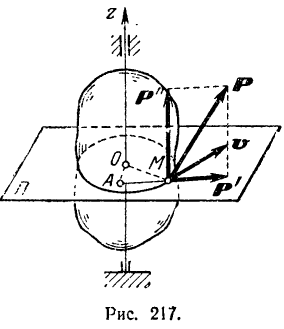
По теореме о работе равнодействующей элементарная работа силы 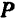равна сумме элементарных работ составляющих сил 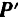и 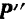. Но сила 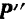направлена перпендикулярно к перемещению точки 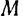, происходящему в плоскости 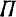, и поэтому ее работа равна нулю. Таким образом, элементарная работа 
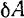силы 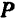равна элементарной работе составляющей :
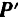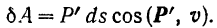
Траекторией точки 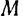твердого тела, вращающегося вокруг неподвижной оси, является окружность радиуса 
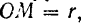и следовательно, элементарное перемещение этой точки 
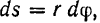где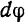 
— элементарный угол поворота тела.
Подставляя значение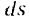 
в выражение для работы, получим:
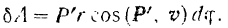
Найдем теперь момент силы 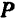относительно оси вращения
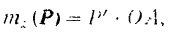
где 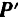— проекция силы 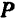на плоскость , 
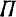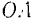— длина перпендикуляра, опущенного из точки 
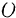пересечения оси 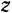с плоскостью 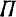на линию действия силы 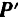. Стороны 
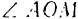перпендикулярны к векторам 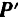и 
и 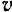поэтому
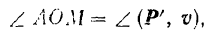
следовательно
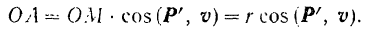
Обозначая момент силы относительно оси вращения тела через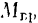 
находим, что
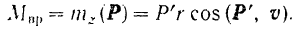
Произведя соответствующую замену в выражении элементарной работы силы 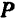, окончательно получаем:
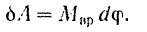
Элементарная работа 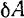силы, приложенной к вращающемуся телу, равна произведению момента 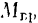той силы относительно оси вращения на элементарный угол 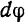повороти тела.
Весь вывод сделан в предположенни, что элементарное вращение происходит в положительную сторону, и момент силы также положителен. Нетрудно убедиться и том, что формула (200j остается верной при любых .знаках 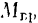и 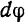если знаки одинаковые, работа положительна, в противном случае она отрицательна.
Работа силы при повороте тела на конечный угол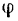 
будет равна
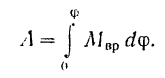
В случае переменой величины момента силы 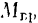для вычисления интеграла (201) должна быть известна зависимость вращающего момента от угла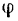
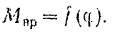
Если же
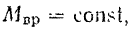
то будем иметь:
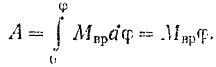
Работа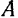 
при постоянном моменте 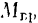силы относительно оси вращения равна произведению этого момента на угол 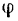поворота тела:
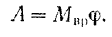
Найдем теперь мощность силы, приложенной к вращающемуся телу, подставив в формулу (197) мощности соответствующее выражение (200) элементарной работы:
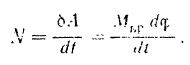
Но
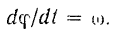
Поэтому
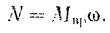
Мощность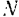 
силы, приложенной к вращающемуся телу, равна произведению момента 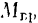этой силы относительно оси вращения на угловую скорость тела.
Если вращающий момент 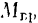выражен в кГм, а угловая скорость 
— в рад/сек, то мощность 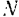, определяемая по формуле (203), будет выражаться в кГм/сек. Если 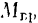, выражен в нм, а 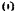— в рад/сек, то мощность, определяемая по формуле (133). будет выражаться в ваттах.
Если приложенная к вращающемуся телу сила 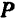направлена по касательной к окружности, описываемой се точкой приложения, то она часто называется окружным усилием.
Очевидно, в этом случае
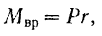
где 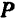— окружное усилие, 
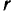— радиус окружности, описываемой точкой приложения этой силы.
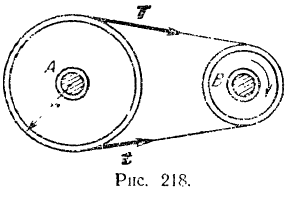
Пример задачи:
Шкив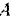 
получает тело шкива 
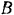при помощи ременной передачи. Ведущая ветвь ремня натянута с силой 
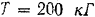, ведомая ветвь — с силой 
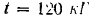. Диаметр шкива 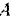равен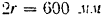 
. Определить работу, совершаемую силами за 10 оборотов шкива , а также передаваемую ремнем мощность (,в лошадиных силах и киловаттах), если шкив делает 120 об/мин.
Решение:
Момент сил относительно оси вращения, приложенный к шкиву:
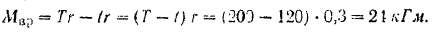
Угол поворота шкифа
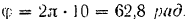
По формуле (202) работа приложенных к шкиву сил
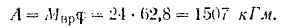
Угловая скорость шкива
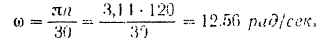
Передаваемая ремнем мощность
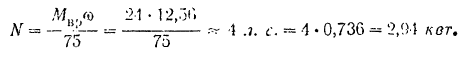
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Работа внутренних сил неизменяемой системы |
| Мощность силы с примером решения |
| Теорема об изменении кинетической энергии точки с примерами решения |
| Кинетическая энергия твердого тела с примерами решения |
