Задача №44.
Пусть ось 
направлена вертикально вверх. Будем предполагать, что на материальную точку действует только сила тяжести. Проекция силы тяжести на ось будет постоянна по величине и имеет отрицательное значение —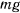
. Поэтому движение материальной точки вдоль оси будет определяться дифференциальным уравнением
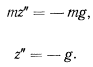
Решение:
Мы будем предполагать, что в начальный момент материальная точка находится на оси и ее начальная скорость направлена вдоль оси . Как известно, при сделанных предположениях точка будет совершать прямолинейное движение, оставаясь все время на оси . Интегрируя дважды дифференциальное уравнение движения, получим закон движения материальной точки при произвольных начальных
который и определяет положение материальной точки в любой момент времени в зависимости от начальных условий. В частности, можно определить момент времени 
, в который точка занимает положение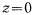 
. Этот момент определяется равенством
Так как время всегда больше нуля, при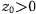 
имеем только одно значение времени , при котором точка достигает положения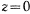 
. Оно определяется формулой
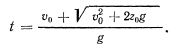
Если же 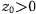, то будем иметь два значения времени , т. е. 
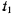и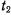 
, в которые точка пересекает начало координат, сначала двигаясь вверх, а затем двигаясь вниз.
Если сила, действующая на материальную точку, зависит только от положения этой точки и по условиям задачи требуется определить изменения скорости в зависимости от положения материальной точки, можно будет воспользоваться теоремой живых сил.
Пусть, например, материальная точка притягивается неподвижным центром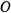 
силой, пропорциональной расстоянию от этой точки до неподвижного центра 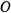. Будем предполагать, что в начальный момент точка находится на расстоянии 
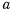от неподвижного центра, а ее скорость равна 
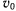и направлена от центра .
Выберем за ось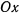 
прямую, проходящую через точку 
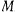. Тогда уравнение движения точки получит вид
где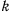 
— коэффициент пропорциональности. Действующая на материальную точку сила 
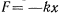обладает силовой функцией 
, а в этом случае, как известно, существует интеграл живых сил
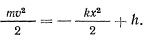
Постоянная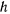 
определяется из начальных условий
Интеграл живых сил определяет зависимость скорости точки от ее положении, а на координату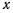 
накладывает условие
откуда получаем
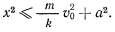
В некоторых задачах силы, действующие на материальную точку, оказываются зависящими от направления движения материальной точки. К таким силам относится, например, сила сопротивления движению точки — сопротивление среды. В общем случае она может быть представлена в виде
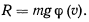
Пусть, например, тяжелая материальная точка движется в вертикальном направлении в сопротивляющейся среде и требуется определить скорость этой точки в зависимости от ее положения. Будем предполагать, что начальная скорость точки равна 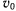и направлена вертикально вверх. Положительную ось 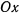направим вертикально вверх, приняв за начало координат начальное положение точки. Уравнение движения для восходящего движения точки получит вид
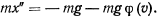
Полагая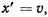 
будем иметь
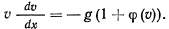
Разделяя переменные и интегрируя, получим
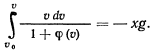
Уравнение определяет движение точки вверх до тех пор, пока ее скорость не обратится в нуль. После этого точка начнет двигаться вниз. Для нисходящего движения уравнение запишется иначе:
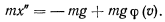
Отсюда получим
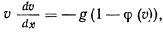
и после разделения переменных будем иметь
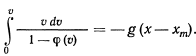
В частном случае, когда сила сопротивления пропорциональна скорости, будем иметь
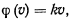
где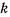 
— постоянный коэффициент пропорциональности. Тогда интеграл, стоящий в левой части, запишется так
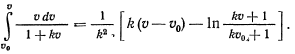
Максимальная высота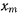 
достигается в тот момент, когда скорость обращается в нуль. Поэтому
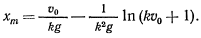
Для определения скорости, с которой точка возвращается в исходное положение, будем иметь уравнение
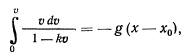
или, после вычисления интеграла левой части,
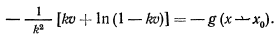
Здесь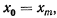 
и точка достигает начального уровня при 
. Так что
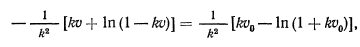
что можно переписать в виде
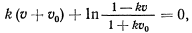
или
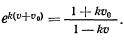
Полученная формула связывает скорость, с которой точка возвращается в первоначальное положение, с той скоростью, с которой точка была брошена вертикально вверх.
Рассмотрим теперь приложение исследованного нами метода к изучению малых движений точки около положения равновесия.
Этот пункт является одним из важных в механике, как наиболее часто встречающийся в технических приложениях.
Общая теория малых колебаний материальной точки приводится во всех курсах теоретической механики. Задача обычно сводится к отысканию решения линейного дифференциального уравнения второго порядка с постоянными коэффициентами. Наибольшие затруднения, по-видимому, представляют вопросы, связанные с. определением сил, создающих колебательное движение, а также составление дифференциальных уравнений, определяющих малые колебания. В простейших задачах линейные дифференциальные уравнения в точности описывают механический процесс. В общем же случае эти уравнения являются лишь приближенными и остаются справедливыми только для достаточно малых колебаний. Методы линеаризации уравнений движения остаются и в настоящее время наиболее простым и эффективным средством решения большей части технических задач.
В качестве простейшей задачи можно рассмотреть задачу о колебаниях материальной точки, подвешенной на пружине и подверженной действию силы тяжести.
Выберем . начало координат в точке подвеса пружины и ось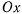 
направим по вертикали вниз. На точку действует сила тяжести 
, проекция которой на ось 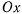положительна и равна , а также сила сопротивления пружины, пропорциональная удлинению пружины. Пусть коэффициент жесткости пружины равен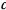 
, а длина нерастянутой пружины — 
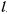. Тогда уравнение движения точки получит вид
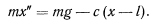
Если ввести новую зависимую переменную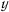 
, определяемую равенством
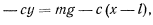
то уравнение это можно будет записать в более простом виде
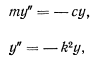
где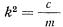 
— положительная величина. Полученное линейное дифференциальное уравнение имеет общее решение
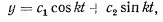
коэффициенты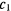 
и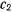 
которого определяются из начальных условий. Если предположить, что в начальный момент пружина не растянута, а точка находится в покое, т. е.
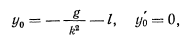
то для определения произвольных постоянных будем иметь условия
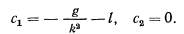
И частное решение, отвечающее этим начальным условиям, запишется в виде:
Оно будет представлять колебательное движение около положения равновесия, в котором
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
