Пусть имеется однородный стержень длины , опирающийся одним из своих концов

Задача №38.

Пусть имеется однородный стержень 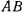длины 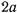, опирающийся одним из своих концов на криволинейную направляющую, имеющую форму окружности радиуса 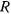(см. рис.31). Пусть этот стержень касается некоторой точки окружности, находящейся в конце горизонтального диаметра. Определить, пренебрегая трением, положение равновесия стержня и исследовать его на устойчивость.

Решение:

Приняв за независимую координату угол , который палочка (стержень) образует с горизонтальным диаметром окружности, будем иметь

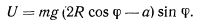
Здесь по условиям задачи

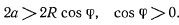
Условия равновесия определяются из равенства

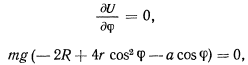
откуда получаем

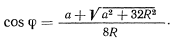
Это решение задачи о равновесии существует, если имеет место неравенство

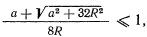
откуда получаем

Неравенство же

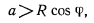
если подставить вместо его значение из условия равновесия, приводит к неравенству

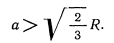
Для определения устойчивости положения равновесия исследуем силовую функцию на максимум. Дифференцируя вторично по , получим

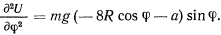
Подставляя сюда значение из условия равновесия, найдем откуда

следует, что найденное положение равновесия устойчиво.

Задача взята со страницы подробного решения задач по всем темам теоретической механики:

Решение задач по теоретической механике

Возможно эти дополнительные задачи вам будут полезны:

Задача №36. Однородный стержень весом может вращаться на неподвижном шарнире в вертикальной плоскости. Конец этого стержня соединен шарнирно с другим однородным стержнем весом . К концу второго стержня приложена горизонтальная сила . Найти углы и стержней с горизонтальным направлением при равновесии системы (рис. 29).

Задача №37. Рассмотрим задачу о равновесии системы, состоящей из шарнирного четырехзвенника , к шарниру которого приложена вертикальная сила , а звено жестко связано с диском, центр которого находится в точке . К диску в точке по касательной приложена горизонтальная сила . Размеры в положении равновесия системы указаны на чертеже. Пренебрегая весом стержней и диска, а также трением в шарнирах, определить соотношение между величинами и в положении равновесия, указанном на чертеже (рис. 30).

Задача №39. Исследовать условия равновесия материальной точки, находящейся под действием силы тяжести, на гладкой горизонтальной плоскости.

Задача №40. Исследовать условия равновесия тяжелой материальной точки, на которую наложены связи (здесь предполагается, что ось направлена вертикально вверх, а ось — горизонтальна).