Оглавление:








Прямозубые цилиндрические передачи
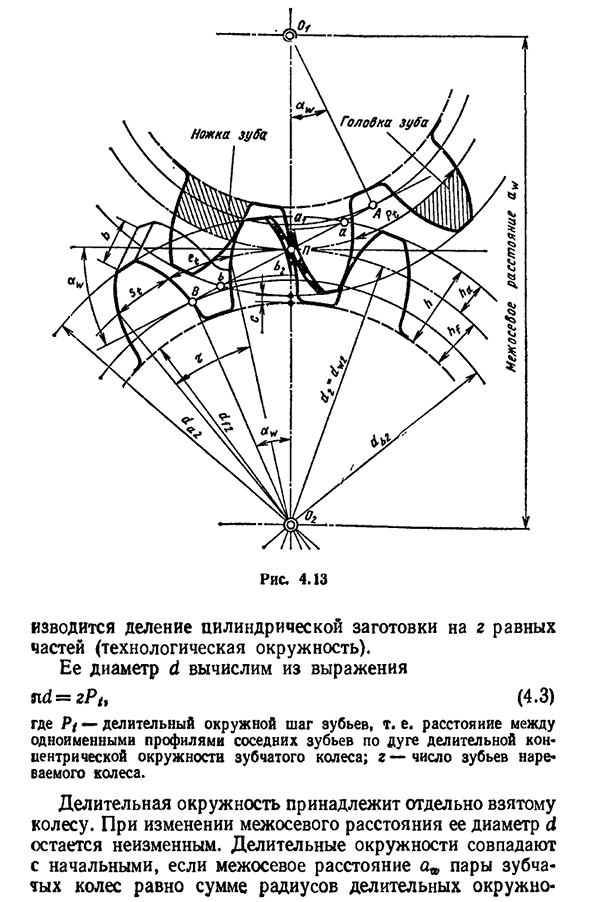
- Цилиндрические шестерни с прямыми зубьями Часть зубчатого колеса, содержащая все зубья, соединенные между собой смежной поверхностью корпуса зубчатого колеса, называется зубчатым кольцом. Геометрические характеристики зубчатой передачи. Форма зубчатой передачи характеризуется концентрическими окружностями вокруг оси зубчатого колеса, расположенными на концах. Различают зубчатое деление, основание, вершину зуба, полость и другие концентрические окружности, каждая из которых принадлежит к зубчатому делению, основанию, вершине зуба, полости и другой коаксиальной торцевой поверхности зубчатого колеса. Они соответствуют диаметрам концентрических окружностей: деление d, главный db, вершина зуба da, впадина df и др. 4.13). Кроме этих окружностей, отдельно рассматривается понятие начальной окружности, ее диаметр обозначается dw. Начальным
называется концентрическая окружность, проходящая через полюс Р, которые перекатываются друг через друга без скольжения в процессе зацепления. При изменении межосевого расстояния золы изменяются и допустимые пределы диаметра шестерни, и начальный круг колеса. В результате пара зубчатых колес может иметь много начальных кругов, определяемых установкой. Там нет первого круга для одного колеса. Согласно рисунку. 4.13 межосевое расстояние аw—(ду,,+у,,)=0,5 ду,,, (1+уу). Деление называется концентрической окружностью, которая проходит в процессе изготовления зубчатого колеса Разделите цилиндрическую заготовку на равные части g (технический круг). Его диаметр d рассчитывается по формуле n d=zP t , (4.3 )) Где-деление окружности окружности шага зуба, р (<Г. Е. деление зубчатого колеса на расстояние между одинаковыми профилями соседних зубьев по дуге концентрических окружностей; Разделительный круг принадлежит одному колесу.
При изменении межосевого расстояния диаметр d остается неизменным. Если расстояние между центрами пары зубчатых колес равно сумме Людмила Фирмаль
радиусов делительного круга,то Делительный круг совпадает с первым.- 74 (4-4))) STEI, ie° » I>-0.5(41+4A)=0.5 di(1+Wia). Выражение (4.3) записывается как d= — ^z; a=mtz, Здесь mt-модуль деления окружности зуба, который является основным расчетным параметром и представляет собой рациональное число L/L. Таким образом, окружной Делительный модуль МТ зубьев называется линейной величиной, в L раз меньшей, чем разделенный окружной шаг (ГОСТ16530-70). Если формула (4.4) записана как mt=d/g, то модуль деления окружности можно рассматривать как часть диаметра делительной окружности на зуб. Модуль измеряется в миллиметрах, и модуль является главной особенностью размера зуба, который используется при расчете и измерении зубчатых колес. Для пары
взаимодействующих колес модули должны быть одинаковыми. Для обеспечения взаимозаменяемости зубчатых колес и унификации зуборезных инструментов величина mt регулируется СЭВ 3-76. Рядок 1: 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20… . Рядок 2: 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14; 18; 22… . При выделении модулей строка 1 должна отдавать приоритет строке 2. Из вышеизложенного видно, что диаметр делительного круга зубчатого колеса равен произведению числа зубьев на стандартный модуль. Окружной шаг зуба на делительном круге зависит от толщины зуба st и ширины полости et: P t=st -} — e(. Для пары сцепленных колес шаг деления
- окружности должен быть одинаковым. Толщина зубьев st и ширина полости et теоретически равны. На практике можно уменьшить число зацепляемых зубьев, которое определяется отклонением предельного размера, компенсируя возможные неточности в изготовлении и изменения линейных размеров в результате нагрева колеса. Главный srg R измеряется в основном круге. Расстояние, основанное на третьем свойстве эвольвенты Обычное расстояние между одинаковыми профилями соседних зубьев будет равно шагу P(см. рис. 4.10). Из треугольника Ogap или O2VP (см. рис. ДБи=Ди, потому что ЗПБ=зпт потому что(4.5)) 4.13 Р* = Р<С О СА,и может быть написано. (4.6) угловой шаг зуба t называется центральным углом концентрической окружности зубчатого колеса, равным 2l/g или 3607 G. Разделительный круг делит зубы на головку и ножки, а их высота
обозначается соответственно ha и hf. В этом случае возьмем ha=mt, hf=1.25 mt, а здесь высота зуба h=ha+hf=2.25 PC. Разница между высотой зубьев ножки одного колеса и высотой головки другого необходима для образования радиального зазора с c-hf-ha=Q, 25mt. Максимальное расстояние между концами зубьев колеса называется шириной коронки, обозначаемой В. Основными параметрами прямого зубчатого колеса, выраженными через модуль, являются однозубые Pt=nmt’, st=et-nmt/2\h=2.25 mt;ha=mt\hf=1.25 mz;c=0.25/nf, колесо концентрическое d=mtz\da=d —
[- 2ha=mtz4-2mt=m (z-f-2); df=колесная пара o=(di) o=(di) 2 ds=di-di-2{■1)/2 = — m iz I(WJ.24- 0 /2 Людмила Фирмаль
=mtzx/2, (4.8) Где G2=4-G2 — общее количество зубов. Зная Zs, определите число зубьев шестерни GX — =G2/(P12 4-1) и колеса G2=G2-G. Согласно формуле (4.5), диаметр основной окружности db=-d cos aw, а согласно формуле (4.7), диаметр окружности впадины df=mt (z-2,5). Если уравнять эти выражения, то получим d cos и y-mt (z-2,5).mtz cos=mt (z-2,5); z= —— __ 75 2 1-COS » a, 1-COS20° 7 » следовательно, когда число зубьев в колесе больше 41, диаметр основного круга меньше диаметра круга углубления, и контур зуба может быть нарисован эвольвентой G<41,диаметр основного круга больше диаметра круга углубления, и только часть контура зуба вне части контура зуба внутри основного круга очерчена переходной кривой, которая не
удовлетворяет требованиям основной теоремы сцепления. Активная линия взаимодействия. Как упоминалось выше, зубчатая линия представляет собой отрезок AB, представляющий собой траекторию общей точки контакта зуба двух сопряженных между собой зубчатых передач(фиг.Пожалуйста, взгляните на него. 4.13). В этом случае отрезок AB определяет предельную длину линии зацепления. Во внешней передаче эвольвентный профиль сопряжен только в пределах отрезка АВ зубчатой линии, заключенного точкой контакта с главной окружностью (точки А и в, следовательно, вне линии зацепления, нарушают основную теорему зацепления. Активная линия зацепления является частью сегмента ab линии зацепления AB. Активная линия зацепления прорезается по прямой линии межд
у окружностями вершин сопряженных зубьев. Длина активной линии зацепления обозначается буквой ga. Активная поверхность и профиль зуба. Активной поверхностью зуба является боковая часть зуба, в которой происходит взаимодействие с зубчатыми сторонами пары колес. Активный профиль зуба является частью профиля зуба, соответствующего активной поверхности. Таким образом, профиль головки зуба полностью участвует в зацеплении зуба на конъюгате. Профиль зубов лапы не полностью участвует в зацеплении. Часть профиля, в которой происходит фактический контакт сопряженного
зуба, является его активной частью. Для определения границ активного участка профиля (его верхней и нижней точек) необходимо найти точки сопряжения ножек зубов на вершине парных зубов. Поэтому, чтобы найти активную часть профиля зубьев на обоих колесах, нужно пройти через начало и конец активной линии Зацепитесь (через точки a и B) сделайте дугу: от центра радиуса RSA точка alt A соответствует профилю ваших зубов в точке b2 (4.13). Понятие интерференции. При увеличении диаметра окружности
вершины возможно увеличение активного профиля зуба. Однако, когда окружность вершины одной шестерни пересекает линию зацепления за пределами точки разрыва A или B, контур головки одного зуба шестерни является вторым Хо вне линии зацепления (4.14). Колеса застревают. Отсутствует внешнее зубчатое зацепление (заклинивание) и следующее соотношение числа зубьев на колесах для колес: Z1 ГГ 13 14 15 17 и более<1 7<2 7<4 8 любой Для колес с внутренними зубчатыми узлами эти соотношения получают следующие значения: «Икс»,,. . 17 18 20 24 25 27… 29 80. %. . . . . И еще>144 > 60 > 38 > 3 5 > (zt — |-8)>(zr — / -7) Обещают скольжение и
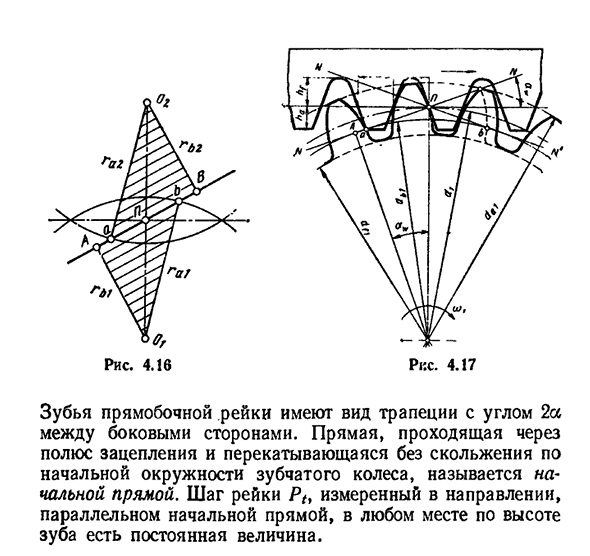
трение. В момент контакта с (рис. 4.15, а) наблюдается перекатывание и скольжение зубьев. Скорость скольжения профиля зависит от формулы с. скорость скольжения в любой точке контакта двух сопряженных профилей, из которой можно определить K=£((0^. (4.Y) для прямозубых передач рекомендуется EA3=1,2. Полученное выражение (4.10) ограничено в использовании, поскольку его можно использовать только при наличии графической структуры зацепления. Для аналитического метода определения коэффициентов конечного перекрытия советников используйте рисунок. 4.16, Джорджия=АВ=АП+Р=(АВ-р)+(б-р); г а =Б А+Б-А Б-Б А=Р * А Л-Р Е А Б=7 классы^^;б=р т зта ж — / — РА зта Ж=Ж Ж Ж грех. Поэтому можно написать в конце концов е . Г ГА1-г В1+г + р» — р б я з ы в НМТ потому что Вт. (4.(I)Формула (4.11)может быть использована для определения коэффициентов конечного перекрытия EA в случае неразрезанных зубьев как нормального колеса, так и неподвижного колеса (см.
раздел). Расчет на практике по приближенной формуле EA=[1,88-3,2(1/?! ±1 / 2A) [cos0;(4.12) здесь знак «плюс» внешний,» минус » внутренний редуктор. Из Формулы (4.12) видно, что величина EA зависит от числа зубьев z и угла наклона зуба P (в случае перекоса колеса). Поэтому выгодно использовать колесо с большим количеством зубьев. С увеличением [} окружной шаг Pb t растет, а длина активной зубчатой линии ga остается неизменной. Это является одной из причин ограничения уменьшенного угла[}. Сетка эвольвентной шестерни шкафом. При бесконечном увеличении
числа зубьев колеса останавливаются в стойке, а эвольвентный профиль зубьев становится прямым и перпендикулярным линии зацепления (рис. 4.17). Харрис 4.16 Зубчатые промобоксы полки имеют угол 2а трапециевидной формы между бортами. Прямая линия, проходящая через зубчатый стержень и катящаяся по первой окружности зубчатого колеса, называется первой прямой линией. Тангаж рельса PTT измерен в направлении параллельном к начальной прямой линии, постоянн значение присутствовал в любом месте вдоль высоты зуба.
Смотрите также:
| Теории зацепления | Основы нарезания зубчатых колес. Точность и кпд зубчатых передач |
| Шпоночные соединения | Виды разрушения зубьев и критерии работоспособности зубчатых передач |

