Оглавление:

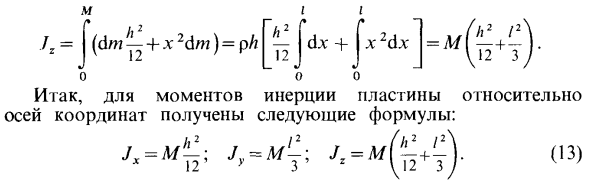

Прямоугольная пластина
- Размеры прямоугольной тонкой пластины — f и h, а масса — M (рисунок 26). Оси Ox и Oy находятся в плоскости пластины, а оси Oz перпендикулярны ей. Чтобы определить момент инерции пластины относительно оси Oy, разделите пластину на основные полосы шириной d.v и массой dwi = p / iax и интегрируйте с x от 0 до /. получить.
Дело в том, что при расчете основной работы возможных и действительных сил не следует путать материальные точки, на которые действует сила, с геометрическими точками ее приложения. Людмила Фирмаль
Потому что фи = М Выполняя тот же расчет для оси Ox, • ‘.- «и- Эта ось Вол проходит через центр пластины. Определить момент инерции Для оси Oz необходимо сначала вычислить момент инерции одиночной заштрихованной полосы для параллельной оси O’z согласно уравнению стержня (12), а затем применить теорему Штейнера. Для основных полос, Формула интеграции Получить в диапазоне от 0 до I Относительно блюдо.
- Поэтому следующая формула получается для момента инерции пластины относительно оси координат. L-AND ^; (13>. Сумма алгебраических моментов для двух силовых точек равна по модулю, действующих вдоль одной прямой, но равна нулю в противоположном направлении.
Он отметил, что маленькие эксцентрические кометы могут описывать очень вытянутые овалы, лежащие на любой поверхности, описывая при этом эллипсы, где планеты лежат почти в одной плоскости. Людмила Фирмаль
Заметим, что векторным моментом силы для точки является вектор, приложенный к этой точке,а векторным моментом силы для остатка произведения силы на плечо силы для этой точки считается вектор, приложенный к этой точке. Вектор момента силы для определенной точки не изменяется от переноса сил вдоль линии ее действия.
Смотрите также:
Задачи по теоретической механике
| Моменты инерции простейших однородных тел | Круглый диск |
| Однородный стержень | Круглый цилиндр |

