Задача №60.
Прямолинейная трубка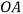 
вращается в вертикальной плоскости вокруг горизонтальной оси 
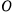с постоянной угловой скоростью 
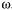. В трубке находится тяжелый шарик массы 
, прикрепленный к пружине, другой конец которой закреплен в точке . Найти закон движения шарика относительно трубки, считая упругую силу пружины пропорциональной ее удлинению с коэффициентом пропорциональности 
. В начальный момент трубка горизонтальна, а относительная скорость шарика равна нулю. Пружина в начальный момент имеет естественную длину 
. Рассмотреть случай
Решение:
Движение шарика происходит относительно вращающейся трубки, поэтому естественно и подвижную систему отсчета связать с трубкой. Направим ось 
по направлению трубки. В подвижной системе на шарик будет действовать кроме силы тяжести и упругой силы еще силы Кориолиса. Сила Кориолиса от переносного ускорения будет направлена вдоль трубки, а по величине будет равна
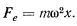
Сила же Кориолиса от добавочного ускорения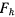 
будет направлена перпендикулярно трубке в сторону, противоположную вращению трубки, а по величине будет равна
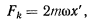
где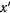 
— скорость точки.
Уравнение движения в проекции на ось получит теперь вид
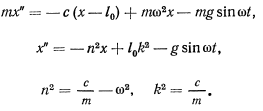
При заданных начальных условиях будем иметь
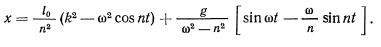
В случае
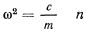
обращается в нуль, и тогда получим другое решение
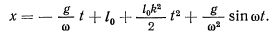
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
