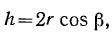Задача №26.
Прямой круговой конус II с углом при вершине 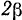 катится без скольжения по внешней стороне неподвижного конуса I с углом при вершине
катится без скольжения по внешней стороне неподвижного конуса I с углом при вершине 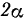 . При этом ось симметрии подвижного конуса вращается вокруг оси симметрии неподвижного конуса с постоянной скоростью угловой
. При этом ось симметрии подвижного конуса вращается вокруг оси симметрии неподвижного конуса с постоянной скоростью угловой 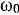 .
.
Определить абсолютное ускорение самой верхней точки М основания подвижного конуса.
Решение:
Воспользуемся теоремой Ривальса и выберем за полюс вершину подвижного конуса, остающуюся неподвижной во все время движения. Будем иметь
Остается определить осестремительное  и вращательное
и вращательное 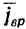 ускорения. Для определения этих составляющих найдем сначала величину и направление вектора мгновенной угловой скорости
ускорения. Для определения этих составляющих найдем сначала величину и направление вектора мгновенной угловой скорости 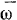 вращения твердого тела. Из геометрических построений
вращения твердого тела. Из геометрических построений
Угловое ускорение 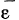 определяется как производная по времени от вектора мгновенной угловой скорости
определяется как производная по времени от вектора мгновенной угловой скорости 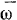 . Нетрудно видеть, что конец вектора мгновенной угловой скорости
. Нетрудно видеть, что конец вектора мгновенной угловой скорости 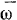 будет описывать окружность вокруг вертикальной оси неподвижного конуса со скоростью
будет описывать окружность вокруг вертикальной оси неподвижного конуса со скоростью
Это и есть скорость конца вектора 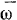 , то есть угловое ускорение
, то есть угловое ускорение 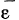 . Таким образом, величина вектора углового ускорения
. Таким образом, величина вектора углового ускорения
Величина вращательного ускорения точки 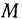 имеет вид
имеет вид
где 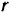 — радиус основания конуса.
— радиус основания конуса.
Нетрудно видеть, что расстояние от точки 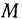 до мгновенной оси вращения равно
до мгновенной оси вращения равно
поэтому для величины осестремительного ускорения получим значение
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
| Задача №24. Окружность радиуса катится без скольжения по неподвижной окружности радиуса так, что скорость ее центра остается постоянной по величине и равна во все время движения. Определить ускорение точки окружности, совпадающей в данный момент с положением мгновенного центра вращения, и ускорение точки , расположенной на противоположном конце диаметра, проходящего через точку . |
| Задача №25. Полый цилиндр радиуса вращается вокруг своей неподвижной оси симметрии с постоянной угловой скоростью . По внутренней поверхности этого цилиндра катится без скольжения другой цилиндр радиуса с постоянной относительной угловой скоростью (как показано на рис. 67). Определить ускорение точки малого цилиндра, совпадающей в рассматриваемый момент времени с осью большого. |
| Задача №27. Диск радиуса катается без скольжения по плоскости, описывая окружность радиуса с постоянной по величине угловой скоростью и сохраняя свою плоскость вертикальной. Найти осе стремительное ускорение и вращательное ускорение точки , положение которой на ободе диска определяется углом . |
| Задача №28. Полиспаст (механизм для поднятия тяжестей, состоящий из двух систем блоков, каждый из которых смонтирован в общей обойме и насажен на отдельные оси, как указано на рис. 1) оснащен нитью, один из концов которой прикреплен к неподвижной точке полиспаста, а другой свободен и находится под воздействием некоторой активной силы . Нить последовательно обходит как подвижные, так и неподвижные блоки. К нижнему блоку подвешен груз весом . Определить соотношение величин силы и веса при равновесии системы. |

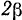 катится без скольжения по внешней стороне неподвижного конуса I с углом при вершине
катится без скольжения по внешней стороне неподвижного конуса I с углом при вершине 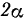 . При этом ось симметрии подвижного конуса вращается вокруг оси симметрии неподвижного конуса с постоянной скоростью угловой
. При этом ось симметрии подвижного конуса вращается вокруг оси симметрии неподвижного конуса с постоянной скоростью угловой 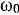 .
.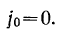
 и вращательное
и вращательное 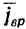 ускорения. Для определения этих составляющих найдем сначала величину и направление вектора мгновенной угловой скорости
ускорения. Для определения этих составляющих найдем сначала величину и направление вектора мгновенной угловой скорости 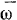 вращения твердого тела. Из геометрических построений
вращения твердого тела. Из геометрических построений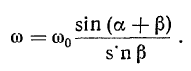
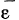 определяется как производная по времени от вектора мгновенной угловой скорости
определяется как производная по времени от вектора мгновенной угловой скорости 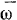 . Нетрудно видеть, что конец вектора мгновенной угловой скорости
. Нетрудно видеть, что конец вектора мгновенной угловой скорости 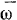 будет описывать окружность вокруг вертикальной оси неподвижного конуса со скоростью
будет описывать окружность вокруг вертикальной оси неподвижного конуса со скоростью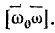
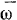 , то есть угловое ускорение
, то есть угловое ускорение 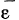 . Таким образом, величина вектора углового ускорения
. Таким образом, величина вектора углового ускорения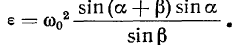
 имеет вид
имеет вид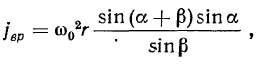
 — радиус основания конуса.
— радиус основания конуса. до мгновенной оси вращения равно
до мгновенной оси вращения равно