Оглавление:











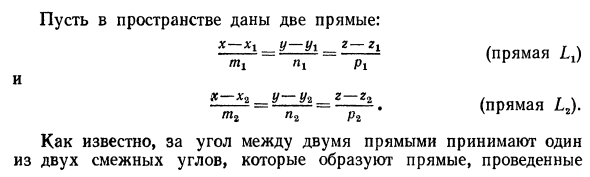



Прямая в пространстве
- ПРЯМАЯ В ПРОСТРАНСТВЕ Уравнения линии в пространстве Линию в пространстве мы будем рассматривать как геометрическое место точек, принадлежащих каждой из двух пересекающихся поверхностей. Если эти поверхности определяются уравнениями Р (х, у, г) = 0 и Ф (х, у, г) = 0, то линия их пересечения определяется система уравнений F (x, у, г) = 0,) Ф (х, у. Г) = 0.) ‘ Например, определяемая при пересечении сферы х * — \ — уг 4- = 25 плоскостью г = 3, определяется промежуточным 2 = 3.
. 2. Общие уравнения прямой Рассмотрим систему двух уравнений первой степени Axx + Bxy + Cxz + Dx = 0, \ d ^ + B ^ -fC ^ -f Da = 0. Каждое из уравнений этой системы изображает плоскость. Если коэффициенты при текущих координатах в этих уравнениях не про-порциональны (т. Е. Если плоскости не параллельны), то система уравнений (12) определяет прямую L, как линию пересечения двух плоскостей, т. Е ….. как геометрическое место точек пространства, координаты которых удовлетворяет каждый из уравнений системы (12) Уравнения (12) называют общие уравнения прямого Примера Построить прямую, заданные общие уравнения: х + у-b * —3 = 0, \ Зу — г + 5 «0.) (И)
Координаты любой точки соответствуют друг другу Людмила Фирмаль
Итак, Мг ^ —3; — ;. Следовательно, канонические уравнения имеют вид х + + 3 _ г —0 3 ~~ —5 —9 J. Уравнения прямой, проходящей через две точки Пусть прямая L проходит через точку МL .. (Jct; ух \ гх) и М2 (хг \ у2 \ Z.2) Составит канонические уравнения этой прямые С этой целью найдет направляющий вектор с прямой, за который принимает вектор, соединяющие точки Мг и Мг: s = МХМ% = (хг — хх) i + (i / a — yY) j + (гг — zx) k. Следовательно, m = x% —xl9 n = y2 — yl9 p = z2-поэтому из уравнений (17) имеем * г — Х \ Уг — Ui гг — гх% v Уравнения (21) называются уравнениями прямой, проходящей через две точки. Пример. Найти уравнения прямой, проходящей через точки AMI; 3; -5) и М2 (1; 4; 2). Решение. Пользуясь уравнениями (21), найдем: х— 1 у — Ъ _ г + 5 1-1 4—3 2 + 5 ‘ ИЛИ х- \ _ у — 3_г-ф 5 0 1 7 * Так как т = 0, то эта прямая перпендикулярная ось х-1 = 0, ^ Ту — г — 26 = 0 *. 6. Угол между двумя прямыми.
Пусть в пространстве даны две прямые: Как известно, между двумя прямыми углами параллельно данным через какую-нибудь точку пространства. Один из этих смежных углов равен углу ср между направляющими векторами с, и данных прямых. Так как Sjss / nxiЧ-WJ + p4kt s2 = MTI + то по известной формуле для косинуса угла между векторами получим Оо = ^ ЦРЦТТЬ ИЛИ — + — (22) V rn \ + n \ + p \ -V т \ + п \ + р \ Условия параллельности и перпендикулярности двух прямых равносильны Условие параллельности.
| Линейные отображения | Прямая и плоскость в пространстве |
| Плоскость | Поверхности второго порядка |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Две прямые параллельны друг другу тогда и только тогда, когда их соответствующие направляющие коэффициенты пропорциональны, т. Е. т1 = п1 = Р1> (23) тг Условие перпендикулярность. Две прямые перпендикулярна друг друг тогда и только тогда, когда сумма парные произведения одно-именной направляющие коэффициенты равны нуль, т. Е. тхтг + пхп% + р ^^ = 0. (24) Пример 1. Найти угол между прямыми х — 2_у + 3_z— 1 лс + 2_ у _ г — 3 5 3 ~~ -2 • 3 2 5 ‘ Решение. Применяя формулу (22), получим 5-3 + 3-2 + (-2) -5 11л OQС \ г.cos ф = -г = ->; = об ~ 0,2895 Y ^ 25 + 9 + 4- ^ 9 + 4 + 25 38 из таблицы находим q> »73 ° 10 ‘. Пример 2. Найти уравнения прямой, проходящей через точку М, (1; 2; 3) прямой прямой 2х + 3 </ + 5г-7 = 0, ^ Зх —4у + г — 8 = 0. I
Решения. Напишите искомое линейное уравнение в канонической форме х-1 у — 2 г — 3 s = N, xN2- = 231 + 13] -17к. (*) T Nj = 2i-f3j 4-5k и N2 = 3i-4j H-k (см. П.4). 1 Дж к 2 3 5 3 -4 1 Следовательно, m = 23, n ^ 13, ρ = -17. Подставляя эти значения для коэффициента направления в уравнение (*) x — 1 y — 2 z — 3 -17 23 13 Пример 3. Найти линейное уравнение через точку Mx (–4; 0; 2) перпендикулярно линии = _ y — 3_z — 5 ~ 2 2 ‘ х — 2 и Напишите линейное уравнение LG-F- 4_Y-0_G-2 t p p ‘ Используйте условие перпендикулярности линии, чтобы получить: 2t-bp + 4 /? = 0, \ 3t- + 2n — {- 2 /? = 0 J Решение этой системы показывает следующее: Точки решения: 3 4 2 2 2 4 3 2 2 3 3 2 = -2k, n = -k = 8 / г, р = рН = к -5 / г Если вы введете k, m = -2, / 1 = 8, p = -5.
Получите вектор направления искомой прямой s как векторное произведение нормальных векторов Людмила Фирмаль
Подставляя найденные значения m, q и p в каноническое уравнение: £ + 4 _ £ _ g-2 —2 «8 -5 Пример 3 может быть решен по-разному, принимая во внимание требуемый вектор направления линии s = min n -f pk. Вектор, перпендикулярный векторам направления sl = 2i-f3j + 4k и s2 = 3i-j-2j + 2k этих линий. В частности, вектор s может быть установлен равным векторному произведению векторов st и s. я J K = −2i −j −8j-5k. 2 3 3 2 S = Sj x s2 = Следовательно, m = –2, n-8, p –– 5.
Решения. Чтобы построить линию, вам нужно знать только две точки. Самый простой способ выбрать эструс — это пересечение прямой и координатной плоскости. Пересечение прямой и координатной плоскости называется прямой линии. Координаты следа Λ |, заданного прямой линией на плоскости Oxu, получаются из уравнения прямой линии, если r = 0. Это дает у = 2 и х = 1. Следовательно, координаты точки Mx: x = 1, y = 2, 2 = 0. Аналогично, если в уравнении задано x = 0, на плоскости Og: Mg (0; 1; 2) Получены координаты трассы M2 линии.
Используйте точки Mx и M2, чтобы создать линию через них. 3. Линейно-векторные уравнения. Параметрические уравнения для прямых Положение линии в пространстве полностью определяется указанием ее фиксированной точки Mt и вектора s, параллельного этой линии. Вектор s, параллельный линии, называется вектором направления линии, а проекция на оси называется коэффициентом направления линии. Предположим, что линия L задана этой точкой (xx \ tjx \ rx) и вектором индукции s = mi-hrtj-f H-pk с факторами направления m, n, p. Рассмотрим любую точку M (x, y% r) на прямой. 86 прямое приобретение с рисунка + 5. (13) Следовательно, вектор MtM на прямой L параллелен вектору направления s (см. Главу III, § 3, 2).
Скалярный коэффициент t% вызываемого параметра может принимать любое значение в зависимости от положения точки M на прямой. Опишите радиус-вектор * точек M и M как yy-OMg и r = OM соответственно, рассмотрите уравнение (14) и опишите уравнение (13) в следующем формате: r = rx + / s. (15) Уравнение (15) называется линейным векторным уравнением. Указывает, что каждое значение параметра t соответствует радиус-вектору точки A1 на прямой линии.
Выражение (15) выражается в формате координат. Заметили r = OM = x \ + y] + zk, rx = OMx = x, i-fx] + rxB и ts = tm \ -f tn] + tpk, Мы получаем х = хх — \ — тм, \ Y = y! + * p, 1 (1G) z = zx + (стр. J Уравнение (16) называется линейным параметрическим уравнением. Когда параметр t изменяется, координаты x% y и r изменяются, и точка M (x, y, r) перемещается линейно. 4. Канонические уравнения для прямых Пусть M (xx \ yx \ rx) — точка на прямой L, а s = mi-f- -fnj + pk — вектор направления линии. Вектор A ^ M, соединяющий точку A1 и переменную точку M (x, y, r) линии L, параллелен вектору s (см. Рис. 86).
Следовательно, проекция вектора MXM и s пропорциональна. MxM = (x-xx) i + (y-tjx) j + (r-zx) k х — хл ==! / -t / x ^ = z — zl (17) tar ‘*’ Следовательно, координаты любой точки на линии должны удовлетворять уравнению прямой, проходящей через эту точку, или уравнению, называемому каноническим уравнением прямой (17). В конкретном случае, когда вектор направления s является единицей, s = i cos «-f j cos f> -f k cosу (Ch. Ill, см. Уравнение (62)), уравнение (17) имеет вид: (18) = y — y y __ 2 — gh cos a cos P cos y Направляющий фактор х.
Вот руководство 87 Косинус вектора с. Уравнение (17) соответствует системе двух уравнений первого порядка. Например, X — Xl_y — ил X — Xx ^ Z — Zx MDCH t ‘p * t’ p Третье уравнение = Z ~ Zy является результатом уравнения (19). В уравнении нет след-координаты Фактически мы определяем плоскость P, параллельную оси Oz (рис. 87).Этот самолет четко проецирует линию L на самолет Оху. X_Xf 2-Z Аналогично, плоскость Q с уравнением m 1 = 1 проецирует линию L на координатную плоскость Ox.
Система уравнений (19) определяет прямую L как пересечение плоскостей, которые проецируют эту плоскость на координатные плоскости Oxy и Oxy. Вместо системы (19) вы можете рассмотреть систему. Или система X — XR — Y — Y1 Y — Y \ r — r, т п ‘п р X-xx _r — 2x Y — Yx __yy, т п * п п * Каждый определяет одну и ту же строку L. Замечания 1. Уравнение (17) можно получить сразу из параметрического уравнения линии (16), удалив параметр /. На самом деле, из уравнения 16, t 9 p r * x— * i , Y — Yx _, g — g или X — Xl = y — yl = Z — 2l mp Замечание 2. Сделайте линию перпендикулярной одной из координатных осей, например, оси Ox. Тогда при m = 0 параметрическое уравнение (17) принимает вид х = хх \ Y = U + W, J (20) z = zx + pt. ) Удаление параметра / из уравнения (20) дает линейное уравнение в виде х — х = 0 Y — Yy_2 — g1 ■
Однако даже в этом случае я согласен формально описать уравнение линии в нормальной форме. * — * 1 y — Y1 g — gh O p r ‘ Напомним, что если один из знаменателей равен нулю в равных отношениях, соответствующий дробный числитель равен нулю. Аналогично, канонические уравнения для прямых Соответствует прямой линии, заданной выражением x-xXY y = yy>. Эта прямая линия параллельна оси Og.
В частности, навес ESSENCE Уравнение оси Оз. В заключение этого раздела рассмотрим вопрос о том, как передать общее уравнение для линии в ее стандартное уравнение. Для этого найдите точку zx) на линии и векторе направления Непосредственно. Линия L задается общей формулой (12) + +0. J * / V, да Рисунок 88 s- = N, x N 2- Координаты точки Mx на прямой L берутся из уравнений (12), а одной из координат задается произвольное значение. Поскольку прямая перпендикулярна нормальным эжекторам N1 = i41 + + BJ + C1cd и Na = A2 \ + Br \ — + Juice (рис. 88), мы можем получить векторное произведение NtxNt для вектора направления s линии L. Я хочу L, Bx CX lg in, ct Давайте рассмотрим конкретный пример. Пример. Дайте общее уравнение прямой 2x до r Zu — 24-8 = 0, ^ x — by — \ — 2r — \ — 1 = 0) В нормальной форме. Решения. Форма канонического уравнения прямой линии: * — * я __ Y — yi ^ r — zx t p r Nt = 21 + 3j-k, Na = i-3j + 2k,
Я хочу 2 3—1 1 -3 2 = 31—5j —9k, s = NtX N2 = Следовательно, m = 3, n = –5, p = –9. Найдите точку M на прямой, задав линию с помощью общего уравнения. Например, z = 0. 2.r + 3y + 8 = 0, \ x — 3y + 1 = 0. J Далее решение этой системы уравнений дает x = –3, y =.

