Оглавление:

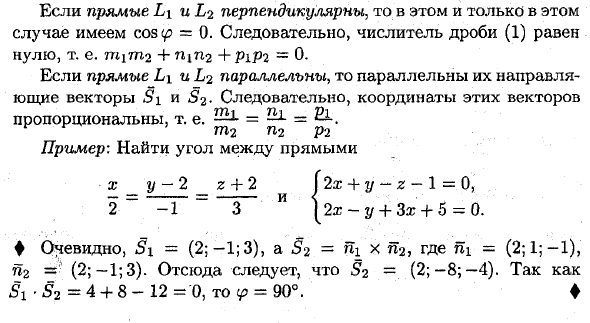


Прямая линия в пространстве. Основные задачи
- Прямая линия в космосе. Основная цель 1. Угол между линиями. Прямая параллельность и условия перпендикулярности Дайте линии L \ и L2 как уравнения X-y-Y \ _ Z-Z \ X до X2 _ Y-y-2 _ z-Z2 ми ни пи т2 п2 п2 Угол между этими линиями дает угол между векторами индукции Si = (wi; ni; pi) и S2 = (rn; или w „y-W \ GP2 + phn2 + P1P2 y / m \ + n \ + pjy / m * + n \ + p2 Чтобы найти острый угол между линиями Li и L2, числитель в правой части уравнения (1) должен быть по модулю.
Если линии L1 и L2 имеют вертикальную ориентацию, это как раз тот случай? = 0 Таким образом, числитель дроби (1) равен нулю, т. Е. S. 77 * 17712 + ritn2 4- P1P2 = 0. Если прямые L \ и L> 2 параллельны, векторы направления Si и S2 параллельны, поэтому координаты этих векторов Пропорционально, т.е. = 2А-. 7712 P2 P’2 Пример: найти угол между линиями £ -Y до 2-2 + 2/2 лет + 2 / — * -1 = 0, От 2 до -1 3 А [2x-t / + Over: + 5 = 0. ♦ Очевидно, 5i = (2; -1; 3) и §2 = fti x P2, где ni = (2; 1; -1), n2 = (2; -1; 3). §2 = (2; -8; -4) §X • S2 = 4 + 8-12 = 0, поэтому ^ = 90 °. ♦
| Плоскость. Основные задачи | Прямая и плоскость в пространстве. Основные задачи |
| Различные виды уравнений прямой в пространстве | Цилиндрические поверхности |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Условия, когда две линии находятся в одной плоскости Дайте прямые L1 и L2 с каноническими уравнениями x-xx _ y-3/1 Z-Z \ X-Xi y-Y2 _ Z-z2 miЩpiГП2п2Р’2 Соответствующими векторами направления являются § \ = (mr, 7ii; pi) и 52 = (m2; n2; p2). Прямая Li проходит через точку Mi (xi; yi; zi) и ее радиус-вектор обозначается через fi. Прямая £ 2 проходит через точку M2 (x2; y2 \ z2), радиус-вектор которой обозначен через r2. тогда r2-fi = VD = (x2-XG, U2-2 / 15 * 2- * i).
Если векторы Si, S2 и M1M2 = f2-fi находятся в одной плоскости, прямые Li и L2 находятся в одной плоскости. Условие векторной компланарности состоит в том, что их смешанный продукт равен нулю: (f2-fi) 5152 = 0, т. Е. X2-Xi Y2-Y \ Z2-251 TTli P \ pi = 0 7712 712 P2 Когда это условие выполняется, прямые Li и L2 находятся в одной плоскости.
То есть они пересекаются для 52 ^ XSi и параллельны для S1 || Людмила Фирмаль

