1) Канонические уравнения прямой имеют вид
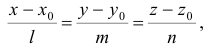
где 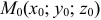 — координаты точки, принадлежащей прямой;
— координаты точки, принадлежащей прямой;
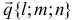 — направляющий вектор прямой.
— направляющий вектор прямой.
2) Из канонических уравнений можно легко получить уравнения прямой в проекциях
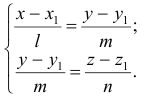
3) Уравнения прямой, проходящей через различные две точки 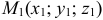 и
и 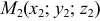 , имеют вид
, имеют вид
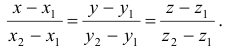
4) Параметрические уравнения прямой получаются из канонических, если принять за 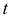 каждое из соотношений
каждое из соотношений
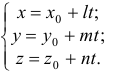
5) Общие уравнения прямой (пересечение двух плоскостей) имеет вид
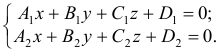
6) Векторное уравнение прямой имеет вид 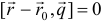 , где
, где 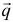 — направляющий вектор прямой;
— направляющий вектор прямой; 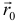 — радиус-вектор точки
— радиус-вектор точки 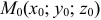 , принадлежащей прямой;
, принадлежащей прямой; 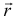 — радиус-вектор произвольной точки
— радиус-вектор произвольной точки 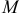 , принадлежащей прямой.
, принадлежащей прямой.
Определение угла между прямыми в пространстве сводится к определению угла между направляющими векторами этих прямых.
Если 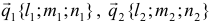 — направляющие векторы, то
— направляющие векторы, то
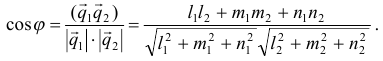
Тогда условие параллельности прямых сводится к условию параллельности направляющих векторов:
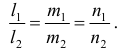
Условие перпендикулярности:
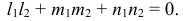
Определение угла между прямой и плоскостью сводится к определению угла между направляющим вектором прямой и нормальным вектором плоскости.
Если 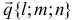 — направляющий вектор прямой,
— направляющий вектор прямой, 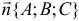 — нормальный вектор плоскости, то
— нормальный вектор плоскости, то
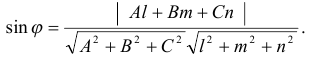
Задача:
Пусть даны точки 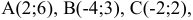
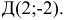
1) Написать уравнения прямых 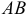 и
и 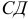 . Определить угловые коэффициенты этих прямых.
. Определить угловые коэффициенты этих прямых.
2) Найти координаты точки их пересечения.
3) Найти угол между этими прямыми.
4) Найти расстояние от точки 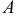 до прямой
до прямой 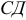 .
.
Решение:
1) Для составления уравнения прямых удобно воспользоваться уравнением прямой, проходящей через две точки (см. гл.З, §2. №4) 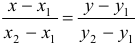
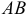 :
: 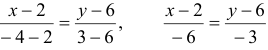 , умножим обе части уравнения на -6, получим
, умножим обе части уравнения на -6, получим 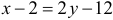 , или
, или 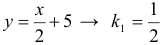
Аналогично получим уравнение прямой  :
:
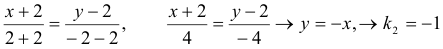
2) Чтобы найти точку пересечения прямых, надо систему уравнений этих прямых.
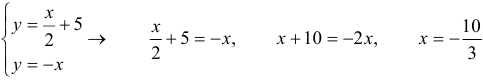 ,
, 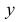 найдем из второго уравнения системы
найдем из второго уравнения системы 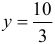 . Ответ:
. Ответ: 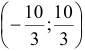
3) Для определения угла между прямыми воспользуемся формулой 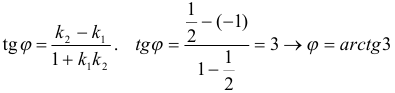 Ответ:
Ответ: 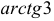
4) Расстояние от точки 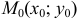 до прямой
до прямой 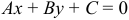 , заданной общим уравнением, вычисляется по формуле
, заданной общим уравнением, вычисляется по формуле 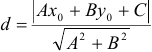 .
.
Запишем уравнение прямой 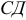 в общем виде
в общем виде 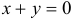 . Имеем
. Имеем 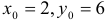 ,
, 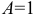 и
и 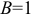 . Подставляем в формулу и получим
. Подставляем в формулу и получим 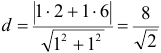 .
.
Ответ: 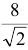
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Различные виды уравнения плоскости |
| Угол между плоскостями |
| Кривые второго порядка: эллипс, гипербола, парабола |
| Исследование общего уравнения кривой 2-го порядка |

