Оглавление:
Прямая линия в пространстве. Основные задачи
Угол между прямыми. Условия параллельности и перпендикулярности прямых
Пусть прямые 
и 
заданы уравнениями
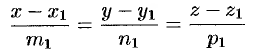
и
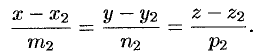
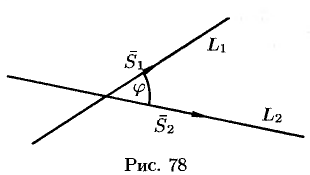
Под углом между этими прямыми понимают угол между направляющими векторами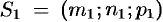 
и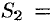 
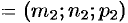(см. рис. 78). Поэтому, но известной формуле для косинуса угла между векторами, получаем 
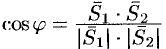или
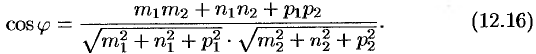
Для нахождения острого угла между прямым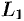и и 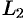числитель правой части формулы (12.16) следует взять по модулю.
Если прямые 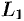и 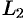перпендикулярны, то в этом и только в этом случае имеем 
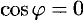. Следовательно, числитель дроби (12.16) равен нулю, т. е. 
.
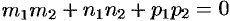Если прямые 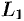и 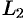параллельны, то параллельны их направляющие векторы 
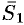и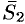 
. Следовательно, координаты этих векторов пропорциональны, т. е. 
.
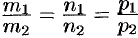Пример №12.2.
Найти угол между прямыми
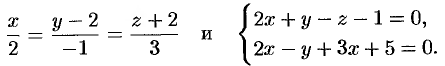
Решение:
Очевидно,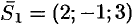 
, а 
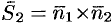, где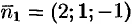 
, 
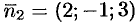. Отсюда следует, что 
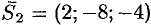. Так как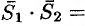 
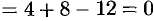, то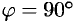 
.
Условие, при котором две прямые лежат в одной плоскости
Пусть прямые 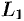и 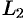заданы каноническими уравнениями
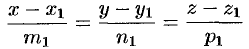
и
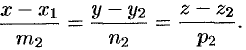
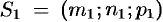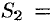
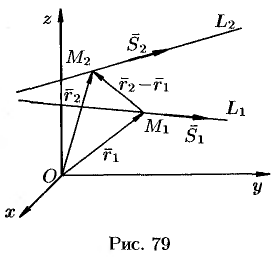
Их направляющие векторы соответственно и 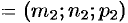(см. рис. 79).
Прямая 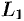проходит через точку 
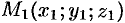, радиус-вектор которой обозначим через 
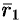; прямая 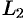проходит через точку 
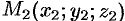, радиус-вектор которой обозначим через 
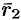. Тогда
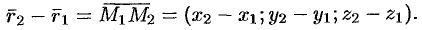
Прямые 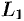и 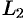лежат в одной плоскости, если векторы 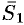, 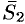и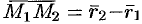 
компланарны. Условием компланарности векторов является равенство нулю их смешанного произведения: 
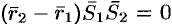, т. е.
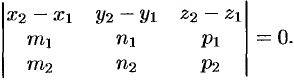
При выполнении этого условия прямые 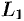и 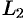лежат в одной плоскости, то есть либо пересекаются, если 
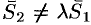либо параллельны, если 
.
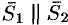На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Плоскость. Основные задачи |
| Уравнения прямой в пространстве |
| Прямая и плоскость в пространстве |
| Цилиндрические поверхности |
