Оглавление:



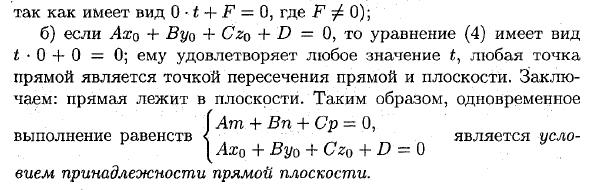
Прямая и плоскость в пространстве. Основные задачи
- Прямо и плоскость в космосе. Основная цель 1. Угол между прямой и плоскостью. Линейный параллелизм и условия перпендикулярности И самолет = 0 и Плоскость Q задается уравнением Ax + F + Cz + D, а прямая L задается уравнением x ~ = Y = r z ~ ZQ. ТП-Ти Д Угол между линией и плоскостью называется одним из двух смежных углов, образованных проекцией на линию и эту плоскость. (P — угол между плоскостью Q и линией L, 0 — угол между вектором n = (A; B: C) и S- = (M; n \ p). Тогда cos # = ‘^. Кроме того, грех — векторы n и S перпендикулярны, поэтому N S • n = 0, то есть Am + Bp + Cp-O Является ли условие параллелизма между прямой и плоскостью.
Поэтому равенство L B S t p r Является условием перпендикулярности прямой плоскости.Пересечение прямой и плоскости. Условия, принадлежащие прямой плоскости Предположим, вы хотите найти пересечение линий X-Xp _ y-y o _ z- ZQ т р р Самолетом Ax + By + Cz + D = 0. (3) Для этого решаем одновременные уравнения (2) и (3). Самый простой способ сделать это — написать уравнение для строки (2) в параметрической форме. х = а? o + y = yo + nt, 2 = Zq + pt.
Если прямая L перпендикулярна плоскости Q, векторы n и 5 параллельны. Людмила Фирмаль
| Различные виды уравнений прямой в пространстве | Цилиндрические поверхности |
| Прямая линия в пространстве. Основные задачи | Поверхности вращения, конические поверхности |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Подставляя эти уравнения для x, y и z в плоское уравнение (3), уравнение A (x0 + mi) + i? (T / 0 + + O (zo + pt) + D = 0 или t (Am + £ n + Cp) + (Al0 + By0 + C-r0 + D) = 0. (4) Если прямая L не параллельна плоскости, то есть Am + Bn + + CpΦ0, найдите значение t из уравнения (4). t _ Ah o -I- ifyo + C ^ o + jP Am + Bn 4- Cp Подставляя найденное значение t в параметрическое уравнение прямой, найдите координаты пересечения прямой и плоскости. Теперь рассмотрим случай Am + Bn + Cp = 0 (L || Q). а) Для Ax o + Boo + Czo + Dф0 прямая L параллельна плоскости и не пересекается (уравнение (4) не имеет решения)
Поскольку 0 • t + F = 0, F равно +0. б) Если Axо + Вуо4-Czo + D = О, то уравнение (4) имеет вид t • О + О = 0, ему удовлетворяет любое значение, а точка на линии является пересечением прямой и плоскости. Вывод: линия проходит в плоскости.
Поэтому одновременно это хорошо Людмила Фирмаль

