Оглавление:
Прямая и плоскость в пространстве. Основные задачи
Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости
Пусть плоскость 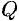 задана уравнением
задана уравнением 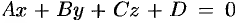 , а прямая
, а прямая  уравнениями
уравнениями 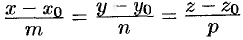 .
.
Углом между прямой и плоскостью называется любой из двух смежных углов, образованных прямой и ее проекцией на плоскость. Обозначим через угол 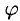 между плоскостью
между плоскостью 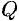 и прямой
и прямой  , а через
, а через 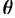 — угол между векторами
— угол между векторами 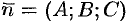 и
и 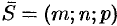 (см. 80). Тогда
(см. 80). Тогда 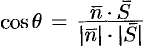 . Найдем синус угла считая
. Найдем синус угла считая 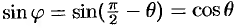 . И так как
. И так как 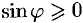 , получаем
, получаем
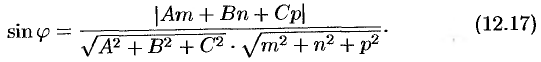
Если прямая  параллельна плоскости
параллельна плоскости 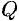 , то векторы
, то векторы 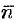 и
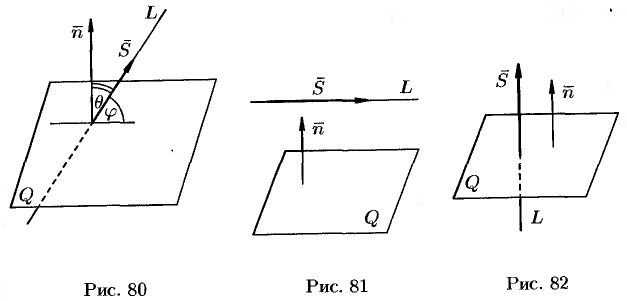
и 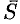 перпендикулярны (см. рис. 81), а потому
перпендикулярны (см. рис. 81), а потому 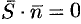 , т. е.
, т. е.
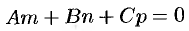
является условием параллельностей прямой и плоскости.
Если прямая  перпендикулярна плоскости
перпендикулярна плоскости 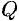 , то векторы
, то векторы 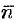 и
и 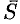 параллельны (см. рис. 82). Поэтому равенства
параллельны (см. рис. 82). Поэтому равенства
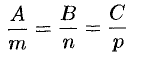
являются условиями перпендикулярности прямой и плоскости.
Пересечение прямой с плоскостью. Условие принадлежности прямой плоскости
Пусть требуется найти точку пересечения прямой
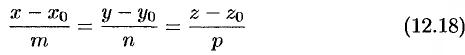
с плоскостью
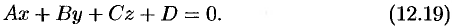
Для этого надо решить систему уравнений (12.18) и (12.19). Проще всего это сделать, записав уравнения прямой (12.18) в параметрическом виде:
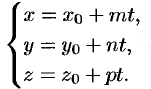
Подставляя эти выражения для 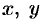 и
и 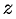 в уравнение плоскости (12.19), получаем уравнение
в уравнение плоскости (12.19), получаем уравнение 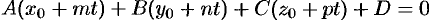 или
или
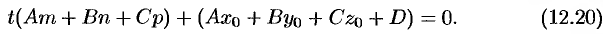
Если прямая  не параллельна плоскости, т. е. если
не параллельна плоскости, т. е. если 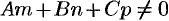 , то из равенства (12.20) находим значение
, то из равенства (12.20) находим значение 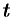 :
:
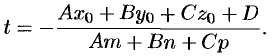
Подставляя найденное значение 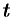 в параметрические уравнения прямой, найдем координаты точки пересечения прямой с плоскостью.
в параметрические уравнения прямой, найдем координаты точки пересечения прямой с плоскостью.
Рассмотрим теперь случай, когда 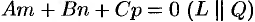 :
:
а) если 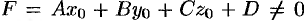 , то прямая
, то прямая  параллельна плоскости и пересекать ее не будет (уравнение (12.20) решения не имеет, так как имеет вид
параллельна плоскости и пересекать ее не будет (уравнение (12.20) решения не имеет, так как имеет вид 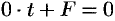 , где
, где 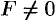 );
);
б) если 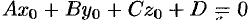 , то уравнение (12.20) имеет вид
, то уравнение (12.20) имеет вид 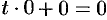 ; ему удовлетворяет любое значение
; ему удовлетворяет любое значение 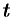 , любая точка прямой является точкой пересечения прямой и плоскости. Заключаем: прямая лежит в плоскости. Таким образом, одновременное выполнение равенств
, любая точка прямой является точкой пересечения прямой и плоскости. Заключаем: прямая лежит в плоскости. Таким образом, одновременное выполнение равенств
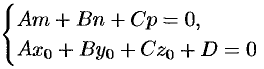
является условием принадлежности прямой плоскости.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Уравнения прямой в пространстве |
| Прямая линия в пространстве |
| Цилиндрические поверхности |
| Поверхности вращения |

