Оглавление:
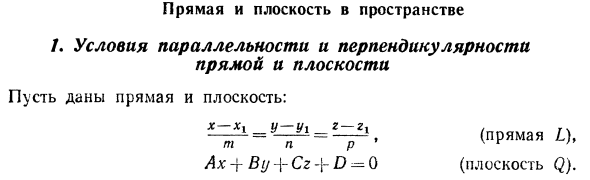







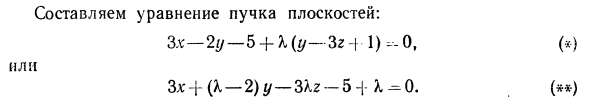
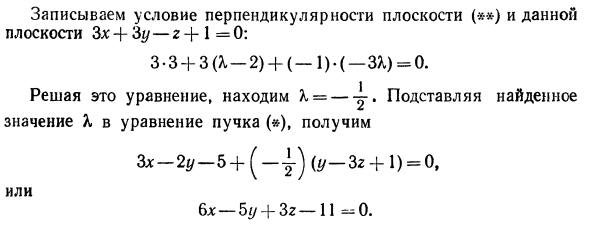
Прямая и плоскость в пространстве
- Космические линии и лица /. Условия параллелизма и перпендикулярности Линии и лица Линии и плоскости даны: х-х, у-у * г-г, -L = -—— = = -1, (прямой т р р ‘в г Ax -f- By Cr D = 0 (плоскость Запишите условие перпендикулярности плоскости (• *) и этой плоскости 3x + 3y-r + 1 = 0. 3-34-3 (L, -2) H — (-!) — (- 3J) = 0. Решение этого уравнения находит X = -y. Подстановка значения, найденного в уравнении карандаша (), дает: 3x-2t / -5 + (- I) (y-b2 + 1) = 0 или 6x-5 // Ch-32-11 = ^ 0.
Вертикальное состояние. A (25) T Условия параллельной обработки. Линии и плоскости параллельны друг другу, только если векторы s и N перпендикулярны друг другу. Это значит Am — \ — Bn + Cp = 0. (26) Пример. Запишите уравнение плоскости через точку M (2; -3; 4), параллельную прямой * y— \ z — 3 d + i y- \ r + 5 1 2 8 4 0 2 *
Прямая и плоскость перпендикулярны друг другу, только если вектор направления прямой s и вектор N нормали плоскости параллельны. Людмила Фирмаль
Решения. Напишите уравнение плоскости через точку Mg: A (* -2) + B (y + 3) + C (r-4) -0 Коэффициенты направления A и B n C могут быть получены из условия параллелизма между плоскостью и прямой (26). М + 2В + 8С = 0, я 4L + 2C = 0. Я Решая эти уравнения одновременности, получаем A — 2, β = 15, C = –4, 2 (x-2) + 15 (0 + 3) -4 (2-4) = 0 или 2 * + \ b-4r + 57 = 0 2. Тонкое пересечение прямой и плоскости Предположим, вы хотите найти пересечение линий (27) м р р 4 ‘ * —X \ Y — Y1 _ гг, Самолетом Ax + By + Cz + D = 0. (28)
Это требует совместного решения уравнений (27) и (28). Самый простой способ это напрямую: (29) Завершить с помощью параметрических уравнений х-хл + тнт, Y = Yx + nt, z = zl + pt. Каждое значение параметра t соответствует точке на линии. Вам нужно выбрать значение для t, где точка линии находится на плоскости (28). Подстановка x, y, r в уравнении (29) в уравнение (28) на плоскости дает следующее уравнение: Значение параметра (: A (Xl + mt) + B (yx + nt) + C (zx + pt) + D = 0, или t (Am + Bn + Cp) = — (i4jct -f Wooh -f Czx + D) Если линия и плоскость не параллельны друг другу, то есть Am 4-Bp 4-CpΦ0, найдите значение t из уравнения (30) Ахг + Вуг + Сгг + П Ат + Бп + вода
| Плоскость | Поверхности второго порядка |
| Прямая в пространстве | Непрерывные функции |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Подстановка найденного значения t в параметрическое уравнение прямой дает координаты пересечения прямой и плоскости. Далее рассмотрим случай Am + Bn + Cp = 0. Как известно, это условие означает, что плоский вектор нормали N = A \ 4-B \ 4-Ck и вектор направления линии s = ml 4-n \ 4-pk перпендикулярны друг другу вы. Здесь возможны два случая. а) Ahg4-Wug + Czx + DΦ0. Это означает, что точка Ml (xl \ yx \ zx) не находится на плоскости Ax — \ — Vy — \ — Cz-f D-0. Кроме того, линия Am 4-Bn 4-Cp-0 и плоскость параллельны друг другу, поэтому единой общей точки не существует.
Тот же результат немедленно следует из соотношения (30). б) Axx — \ — Wu 4-Cr, -f D = 0. Это означает, что точка Mx (xx; yx; zx) находится в плоскости Ax + By + Cz + D-0. Кроме того, поскольку векторы N и s являются вертикальными (Am + Bn 4-Cp = 0), мы заключаем, что линия находится в этой плоскости. Тот же результат можно получить из соотношения (30). (31) Следовательно, равная реализация равенства Am + Bn + Cp = 0, | Axx 4-woof + Czx 4-O = 0 J
Это принимает форму 0-> = 0 в условиях Am + Bn + Cp ~ 0 и Axx 4-Booh 4-Czx 4-D = 0 и выполняется для значения t. Людмила Фирмаль
Дает условие, что прямая * n * 1 = y = находится в плоскости Ax + By — \ — Cz — \ — D = 0. Пример. Найти пересечение линии = ^ il = В плоскости 2x + by-2z 4-2 = 0. Решения. Запишите эту строку уравнений в параметрической форме. x = 2t + \ A Y = 3 / -1, \ 2-2 / -f5. J Подставьте эти уравнения для x, y, r в уравнение плоскости: 2 (2t + 1) -f-3 (3 / -1) -2 (2 / + 5) + 2 = 0 Следовательно, подставляя прямую t = 1 в t-1. Параметрическое уравнение дает * = 2-1 + 1 = 3, // = 3 • 1-1 = 2, r = 2-1 +5 = 7. Пересечение прямой и плоскости — это точка М (3; 2; 7). 3.
Расстояние от тонкой стены до плоской поверхности Предположим, что у нас есть плоскость Q с точкой Mg (xx \ yx \ r) и уравнением. Ax + By + Cz + D = 0. (33) Расстояние d между ними, то есть длина перпендикуляра, упавшего от точки до плоскости Q, определяется по следующей формуле: j Ааа + Ду! + Cr | + P | (34) Вывод аналогичен выводу уравнения для расстояния от точки до прямой на плоскости. Пример. Найти расстояние от точки Mx (\; 0; -2) до плоскости 2x — y + 2z — 4-0. Решения. Из уравнения (34) d = M * 1 + Dn1 + s * | + P1 = il’iz:] ± ‘tUzz2l-41—2 VYv + (- + ^ 3
Хорошо самолёт Множество всех плоскостей, которые проходят через данную прямую линию L, называется плоским карандашом, а прямая L называется осью карандаша. Ось луча задается как L ^ + B ^ + CV + Z ^ O, т L2x + B2 // + C2g + D2 = 0. J Умножьте второе уравнение (35) системы на постоянную I и добавьте к первому уравнению. Axx + Bhu + Cx + Ox + 1 (A2x + B2y + C2g + Og) = 0 (36)
Уравнение (36) является линейным по отношению к n *, y и z, поэтому оно определяет конкретную плоскость для любого числа A. Поскольку уравнение (36) является результатом уравнения (35), координаты точки, которая удовлетворяет уравнению (35), также удовлетворяют уравнению (36). Таким образом, для числа A уравнение (36) представляет собой плоское уравнение по прямой (35).
Указывает, что все плоскости плоского пучка с осью, определенной уравнением (35), могут быть выражены в виде (36), кроме плоскости A2x + C2r + Da = 0. Действительно, плоскость расслоения определяется точкой y \ i) и не будет лежать сверху Ось луча. Чтобы найти уравнение для этой плоскости, замените координаты точки Mx в уравнении (36). AiXx + С1г1 + D, + X (Лгх, + + Саг, + D,) — 0. (37) Из уравнения (37) найдите значение A, если Arxr + B2y1 H-C2r, -f D2 ^ 0, то есть если точка Mx не является второй из этих плоскостей (35). Подставляя найденное значение A в уравнение (36), чтобы получить уравнение для плоскости луча, проходящего через точку Mx.
Таким образом, уравнения с различными значениями X (36) дают уравнения для любой плоскости луча, ось которого задается уравнением (35), за исключением плоскости A2x-L B2y + C2z + Dt = 0. Поэтому уравнение (36) называется карандашным уравнением грани. Уравнение плоского карандаша используется для решения проблемы нахождения плоскости, которая проходит через данную линию, и значение коэффициента X обычно получается из дополнительных условий, которые определяют положение желаемой плоскости. Давайте посмотрим на некоторые примеры.
Пример I. Найти уравнение плоскости через прямую 2x + by-5r + 1 = 0, ^ 3x-y + r H-28 = 0 j И точка М (1; -2; 3). Решения. Напишите уравнение плоского карандаша через эту линию. 2x-3 y-5r H-1 + X • (3x-y + y + 28) = 0. Подставим координаты точки Mt в уравнение расслоения. 2-1 H-3 (-2) -5-3 + 1 + X [3,1 -1 (-2) + 3 + 28] = 0. Статически, подставляя значение X = found X в уравнение пучка, можно найти уравнение искомой плоскости: 2x — \ — by-5rH-1 (3x-y + r — \ — 2b) = 0 Или 7x + на-9z — \ — 30 -0. Пример 2. Найти уравнение плоскости по прямой = = перпендикулярно плоскости Zx’H-3y — z + l = 0 Создайте уравнение плоского пучка: + 1 (у-3р-1) -0, () или 3x- (X-2) y-3X2 -5 4 X-0. (*)

