Проверка выполнимости предпосылок МНК. Статистика Дарбина — Уотсона
Статистическая значимость коэффициентов регрессии и близкое значение коэффициента детерминации В к единице не гарантируют высокое качество уравнения регрессии, поскольку могут нарушаться предпосылки МНК (п. 1.4). Нарушение необходимых предпосылок влияет на точность оценок коэффициентов регрессии, увеличивая их стандартные ошибки, и обычно свидетельствует о неверной спецификации самого уравнения.
При построении линейного уравнения регрессии, мы предполагаем, что реальная взаимосвязь факторных признаков с результативным признаком является линейной, отклонения от линии регрессии являются случайными, независимыми друг от друга величинами с нулевым математическим ожиданием и постоянной дисперсией. Если эти предположения не выполняются, то оценки коэффициентов регрессии не обладают свойствами несмещенности, эффективности и состоятельности, и анализ их значимости будет не точным. Указанные предположения могут не выполняться вследствие нелинейности изучаемой зависимости или при наличии существенного неучтенного фактора в модели. Поэтому на начальном этапе проверяется, как правило, выполнимость статистической независимости оценок отклонений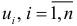 
, между собой. Для этого проверяется коррелированность соседних отклонений 
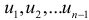, и 
, и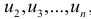спользуя коэффициент автокорреляции первого порядка:
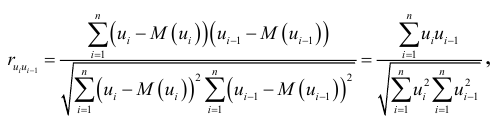
где математическое ожидание
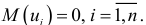
На практике для анализа коррелированности отклонений вычисляют статистику Дарбина — Уотсона:
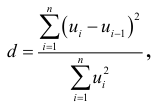
которая связана с коэффициентом автокорреляции равенством
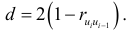
Можно показать, что необходимым условием независимости случайных отклонений является близость к двойке статистики Дарбина — Уотсона: 
. В этом случае считается, что отклонения от регрессии являются случайными и что построенная линейная регрессия, вероятно, отражает реальную зависимость. Для ответа на вопрос, какие значения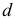 
можно считать близкими к двум, разработаны таблицы критических значений статистики Дарбина -Уотсона. В таблице, по данному числу наблюдений 
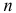, количеству факторов 
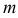и заданному уровню значимости 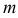, определяются два числа: 
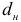— нижняя граница и 
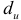— верхняя граница, которые устанавливают границы приемлемости расчетной статистики 
.
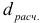Если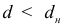 
, то существует положительная автокорреляция остатков; 
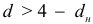, то существует отрицательная автокорреляция остатков; 
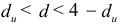, то автокорреляция остатков отсутствует; 
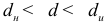или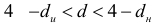 
, то гипотеза об отсутствии автокорреляции не может быть ни принята, ни отклонена.
При наличии автокорреляция остатков уравнение регрессии считается неудовлетворительным.
Заметим, что если выполняется неравенство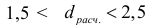 
, то можно приближенно считать, что автокорреляция остатков отсутствует.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:
