Оглавление:






Проверка тонкостенных стержней открытого профиля на устойчивость.
- Проверка тонкостенных стержней с открытыми профилями на устойчивость. В XXX главе Б. был дан вывод основной формулы теории 3. Власова для расчета нормальных и касательных напряжений при кручении и изгибе тонкостенных стержней. Особой проблемой является расчет устойчивости сжатых тонкостенных стержней открытого (открытого) сечения, применяемых в авиационных и других конструкциях(рис. 577). Теория упругой
устойчивости Фигура. 577. & Теория такого стержня представлена в специальном курсе устойчивости упругой системы. Этот пункт является пунктом B. 3. Приведите только часть конечного результата, полученного путем. Власов в исследовании устойчивости тонкостенных стержней. § 182, явление скручивания
тонкостенного стержня происходит не только при его скручивании или изгибе Людмила Фирмаль
боковыми силами (не проходящими через центр изгиба), но и на конце стержня. Из этого следует, что кручение, связанное с неравномерным истощением участка и возникновением нормального напряжения сектора, играет важную роль в случае потери устойчивости из-за тонких стержней 666 более сложных задач испытания на устойчивость[глава XXXIV]. На самом деле, V. решение, полученное по 3. При изучении устойчивости тонкостенных стержней Власов указывает, что в наиболее распространенных
случаях потеря их устойчивости происходит в изогнутой изогнутой форме. Для случая Центрального (осевого) сжатия тонкостенного стержня продольной силой получено дифференциальное уравнение для его криволинейной оси. 3. Имеют вид (рис. Пятьсот семьдесят восемь): EJz^+п л»+А Г р г «=0-1EJJin+(пр*-ГДж в J0«+аз Р\ «- АУ РФ » =0. (34.33) В этих равновесиях в основном Стержень, уравнение
- плоскости В л г Величины, связанные с изменением основных форм, имеют значения: Ejy и EJZ-жесткость инерционного стержня; EJ^и GJK-жесткость на кручение сектора и стержня; и$—дополнительное смещение в направлении оси y и 2.( Из уравнения (34.33) следует, что если AU и AG не равны нулю, то член, содержащий 0 во всех выражениях, не равен нулю, и потеря устойчивости таких стержней сопровождается закруткой, поэтому стальные стержни, центр кривизны которых отсутствует ни в одной из главных инерционных
осей (AU T£0 и 0,0), всегда имеют тонкие сечения * По~ _ — главе J7. — / Фигура. 578 для такого стержня, исходя из решения уравнения(34.33), критическая сила тонкостенного стержня меньше, чем полученная по формуле Эйлера, и ее применение можно отнести к грубому просчету. Эта ситуация имеет большое практическое значение и может быть объяснена также физически. В теории Власова гипотеза плоского сечения не используется; в теории Эйлера на практике имеется дополнительное соединение по всей
длине стержня (плоское сечение). Отсюда следует, что критические силы, вычисленные Людмила Фирмаль
по формуле Эйлера, обычно больше тех, которые найдены теорией Власова, что подтверждается опытом. Если OU=0 и o2=0, то есть центр изгиба совпадает с центроидом сечения, то уравнение (34.33) принимает вид: £J25iv+p «» =0;| ^У1+^’=0;| EJjF+(Pr2-GJ0 ″ =0. ) (34.34)§ 2 1 3] испытание тонкостенных стержней на устойчивость 667 В этом случае в первых двух уравнениях терм, содержащий 0, равен нулю. Эти уравнения соответствуют изгибу изогнутой формы. Третье уравнение не зависит от величины$и 1, поэтому оно соответствует потере устойчивости в чисто крутильной форме. В шарнирной опоре на конце стержня, в результате интегрирования и использования граничных условий, вычисленные корни этого уравнения имеют значение: (34.35)) P v и RG-критические силы Эйлера,
соответствующие изгибу стержня в обеих главных инерционных плоскостях. RF является важной силой, которая соответствует потере устойчивости чисто торсионной формы. Для сечения с одной осью симметрии (например, ось y)T корень V дифференциальных уравнений.3. Будет Власов(34.33): «»tjejz Pt=P2= — — — — критическая сила Эйлера;2 1__(Ru+L>) G2±U(P u+P^g — 4P, P W(g — A * y) g*P S J-2 (g’ — a’) (34.36) в этом случае форма потери устойчивости выглядит следующим образом: Три корня дифференциального уравнения 3. Критические силы Власова(то есть силы Pi, P2 и P8) следует считать минимальными. Согласно теории и опыту, в случае тонкостенного стержня с номинальной осью поперечного сечения пара сила Р8 под действием изгиба стержня теряет устойчивость крутильной формы, как правило, наиболее важную. Для сравнения значений
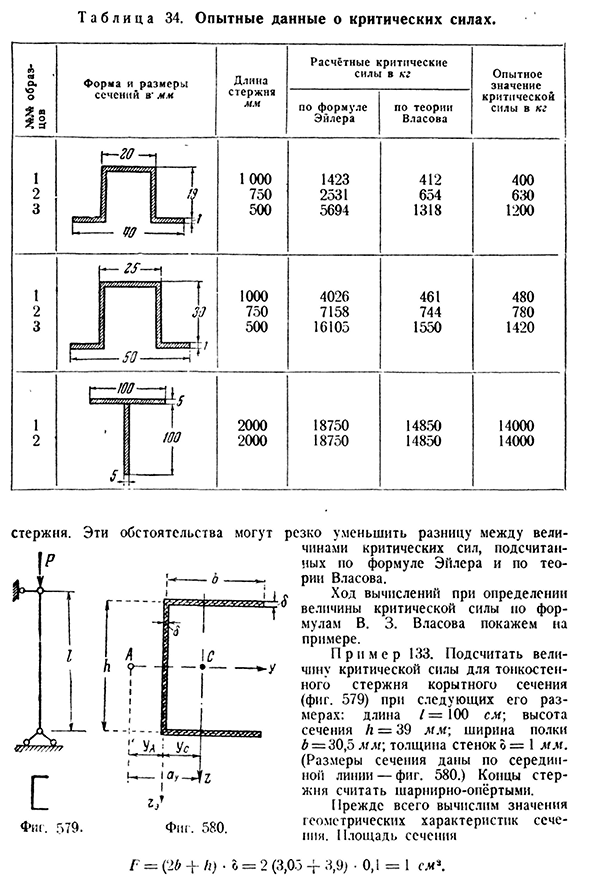
критических сил, рассчитанных по формуле Эйлера и Формуле Власова, и сравнения полученных результатов с экспериментальными данными в таблице 34 приведены осевые усилия, выполненные в лабораториях ЦАГИ и ЦНИИПС. Как видно из таблицы, экспериментальные значения критических сил всех испытуемых стержней основаны на теории B. It находится в хорошем согласии с результатами, полученными по 3. Власов, Власов величина критической силы гораздо меньше Эйлера. Но результат, приведенный здесь, — это B. 3,который будет выпущен в ноябре. Власов был получен из состояния свободного истощения концов.
На самом деле, при фиксации конца сжатого стержня способом, который обычно или другим способом, эффект торсионного эффекта под действием продольных сил значительно усиливается далее, во многих случаях наличие соединительных стержней и решеток приводит к закрытым профилям открытого профиля, что приводит к опасному эффекту скручивания Таблица 34. Экспериментальные данные по критической силе. Эти ситуации могут резко уменьшить разницу между Формулой Эйлера и величиной критических сил, рассчитанных по теории Власова. Формула В. 3. процесс расчета при определении величины критической силы. Власов приводит вам пример. П р и М Е Р133. Рассчитайте значение критической нагрузки для тонкого стержневого желоба (рис. 579) в следующих размерах:
длина Z=100 см; высота h=39 мм; ширина полки#=30,5 мм; толщина стенки o=1 мм. 580)концы стержней считаются шарнирно-опорными. Во-первых, вычислите значение геометрической характеристики сечения. Поперечное сечение G=(2#+h• * o== 2 (3,05 4- 3,9) • 0,1 = 1 Ссылка.§ 2 1 3] испытание тонкостенных стержней на устойчивость 6€6 Расстояние до центра тяжести от оси сечения S_2i ’ 6_g ’3, 05s_N L, Y s~F «2 (2+L)6″2+L— 2 • 3,05 + 3,9″ 0.!См. w’moment инерции сечения относительно главной центральной оси J y и Jz. + 0^+м с Б Ш!91=2>815L=L5 — ^+2[^4-m (4-us) 2]= =3,9 — 0,1 — 0,93 s+ 2 [ ° ’^ ’1 2 ’0 0 * 4 — 3,05 — 0,1 — 0,9 h) 2]=1,027 см. Расстояние мула (30.42):
от оси z Q до центра сечения изгиба (см.§ 181, передняя часть-_3£2_3•3,052 , _ Ул-6С+л— 6 • 3,05 + 3,9 — — видишь? Расстояние от главной центральной оси до центра изгиба: ^=0; +В С-1,257.+0,93=2,187 см. Новые характеристики раздела G2= / jl+L4 -=?L15 — ±1 ′ 92_7+2,187 s=8,625 СМ1. Главный момент инерции сечения, рассчитанный для профиля желоба (см.§ 181), g2L+ 3£_ 3,05′ • 3,92 • 0,1 (2 • 3,9 + 3 • 3,05) _O7u1o J, 12L+ 6 * «12(6-3,05 + 3,9) — 2,/4» э-л. Крутящий момент инерции: Тонны \л ы О3 1,12(2ч+л)?? = — С2- (2 • 3,05 + 3,9) — 0,1′ = 0,00373 да. СМ* Значение жесткости стержня (коэффициент силы): сила Эйлера на плоскости наибольшей
жесткости п г= ^=9!8 и 7. 2. 7 10’:2,815=z5 5 5 0 1002 Крутильный эффект соответствует силе φ — =i’ >0′ ■ 0.00373) = 073 1002 кг. Отсюда уравнение B. Все значения, входящие в 3. Власова, Делани oire-6 7 0 более сложные вопросы теста стабильности[глава XXXIV Значение критической силы Власова (34.36): (Ru+ * g2-u[(ru+R W) * g — 4-Rursh(g — (5550+975)•8,625 2(8,625-2,1872) В[(5550 + 975)2 • 8,625 — 4.5550.975 (8,625 — 2,1872)] 8,625 , 2(8,625-2,1872) Для возможных примеров значение критической силы Власова 2025n o «» ~было меньше, чем у Эйлера—=2,3 раза. Это означает, что опасное рабочее состояние расчетного стержня возникает при значительно меньшей нагрузке, чем предполагается на основании формулы Эйлера.
Смотрите также:
| Обоснование расчёта соединительной решётки в составных стержнях. | Развитие расчётов на устойчивость |
| Примеры расчёта сжато-изогнутых стержней | Учет сил инерции и колебаний. Введение |

