Проверка существенности оценок параметров регрессии, коэффициентов корреляции и детерминации
Мы отмечали, что оценки параметров регрессии являются случайными величинами с определенными распределениями вероятностей. При выполнении предположений 1 — 6, указанных выше, оценки параметров регрессии 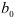 и
и 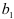 , распределены нормально с математическим ожиданием
, распределены нормально с математическим ожиданием
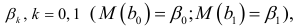
и дисперсией
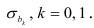
Отсюда следует, что величина
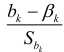
имеет стандартное нормальное распределение. Значения распределений оценок параметров регрессии позволяют производить оценку значимости соответствующих статистических характеристик. При практических исследованиях проверка значимости основывается на выборочных наблюдениях. Как всякая статистическая характеристика, параметры уравнения регрессии являются величинами случайными, т.е. их значения случайно рассеиваются вокруг одноименных параметров генеральной совокупности (истинных значений параметров теоретической регрессии). Если значения оценок параметров эмпирической регрессии попадают в зону рассеяния, обусловленную случайным характером самих показателей, это не является доказательством отсутствия регрессионной связи. Можно только утверждать, что исходные данные не отрицают отсутствия связи между переменными.
Но если значения оценок параметров регрессии будут лежать вне этой зоны рассеяния, то можно считать, что между переменными существует статистически значимая связь. Используемый для решения этой задачи критерий значимости основан на распределении различных статистик.
Практически проверка значимости начинается с формулировки нулевой гипотезы 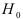 состоящей в том, что между параметром выборки и параметром генеральной совокупности имеется существенное различие. Альтернативная гипотеза
состоящей в том, что между параметром выборки и параметром генеральной совокупности имеется существенное различие. Альтернативная гипотеза 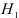 утверждает, что между этими параметрами не имеется существенного различия. Затем устанавливается уровень значимости
утверждает, что между этими параметрами не имеется существенного различия. Затем устанавливается уровень значимости 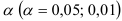 , выражающий вероятность того, что нулевая гипотеза
, выражающий вероятность того, что нулевая гипотеза 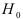 отвергается в то время, когда она в действительности верна. При проверке существенности параметров корреляционно-регрессионной связи выборочную характеристику, вычисленную по результатам наблюдений, сравнивают с соответствующим критическим значением. При этом следует различать одностороннюю и двустороннюю критические области. Форма задания критической области зависит от постановки задачи. Если требуется оценить абсолютную величину расхождения между параметрами выборки и генеральной совокупности, то используется двусторонняя критическая область. Если же требуется установить, что один из параметров строго больше или меньше другого, то используется односторонняя критическая область. Уровень значимости, при использовании односторонней критической области меньше, чем при использовании двусторонней. В случае симметричного распределения выборочной характеристики уровень значимости двусторонней критической области равен
отвергается в то время, когда она в действительности верна. При проверке существенности параметров корреляционно-регрессионной связи выборочную характеристику, вычисленную по результатам наблюдений, сравнивают с соответствующим критическим значением. При этом следует различать одностороннюю и двустороннюю критические области. Форма задания критической области зависит от постановки задачи. Если требуется оценить абсолютную величину расхождения между параметрами выборки и генеральной совокупности, то используется двусторонняя критическая область. Если же требуется установить, что один из параметров строго больше или меньше другого, то используется односторонняя критическая область. Уровень значимости, при использовании односторонней критической области меньше, чем при использовании двусторонней. В случае симметричного распределения выборочной характеристики уровень значимости двусторонней критической области равен 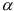 односторонней
односторонней 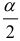 .
.
Затем задается статистическая характеристика (статистика) для проверки гипотезы 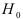 . Более подробное теоретическое обоснование проверки статистических гипотез можно найти в учебном пособии (2, § 8.1).
. Более подробное теоретическое обоснование проверки статистических гипотез можно найти в учебном пособии (2, § 8.1).
Рассмотрим проверку значимости параметров корреляционно-регрессионного анализа. Для оценки значимости каждого параметра регрессии выдвинем следующие гипотезы:
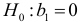 — переменная
— переменная 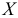 не оказывает существенного влияния на зависимую переменную
не оказывает существенного влияния на зависимую переменную 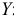 ;
;
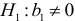 — переменная
— переменная 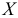 оказывает существенное влияние на зависимую переменную
оказывает существенное влияние на зависимую переменную 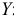 .
.
При такой альтернативной гипотезе 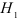 используется двусторонняя критическая область. Если же альтернативная гипотеза
используется двусторонняя критическая область. Если же альтернативная гипотеза 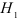 формулируется в виде
формулируется в виде 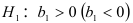 т.е. имеется значимая положительная (отрицательная) зависимость переменной
т.е. имеется значимая положительная (отрицательная) зависимость переменной 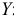 от переменной
от переменной 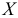 , то используется односторонняя критическая область. Ясно, что при такой формулировке альтернативной гипотезы на основании экономических соображений должен быть априори известен знак параметра регрессии.
, то используется односторонняя критическая область. Ясно, что при такой формулировке альтернативной гипотезы на основании экономических соображений должен быть априори известен знак параметра регрессии.
Для проверки гипотезы 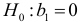 используется статистика
используется статистика
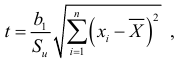
а гипотезы 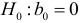 — статистика
— статистика
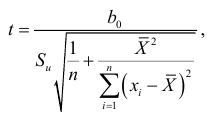
подчиняющиеся распределению Стьюдента с 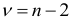 степенями свободы; а
степенями свободы; а 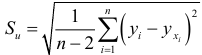 — стандартная ошибка регрессии.
— стандартная ошибка регрессии.
Проверяя значимость коэффициента парной корреляции, устанавливают наличие или отсутствие корреляционной связи между исследуемыми экономическими явлениями. При этом выдвигаются следующие гипотезы:
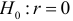 — между переменными
— между переменными 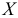 и
и 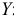 отсутствует значимая корреляционная связь;
отсутствует значимая корреляционная связь;
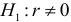 — между переменными
— между переменными 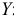 и
и 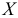 имеется существенная корреляционная связь.
имеется существенная корреляционная связь.
Из альтернативной гипотезы следует, что нужно воспользоваться двусторонней критической областью.
Для проверки гипотезы 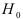 по результатам выборки используется статистика
по результатам выборки используется статистика
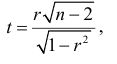
распределенная по закону Стьюдента с 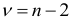 степенями свободы.
степенями свободы.
Вычисленные по результатам выборки статистики (1.4) — (1.6) сравниваются с критическим значением, определенным по таблице распределения Стьюдента при заданном уровне значимости 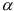 и
и 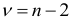 степенях свободы. Если
степенях свободы. Если 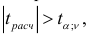 то нулевая гипотеза
то нулевая гипотеза 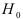 отвергается, т.е. корреляционно-регрессионная связь между переменными
отвергается, т.е. корреляционно-регрессионная связь между переменными 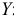 и
и 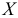 значима; если же
значима; если же 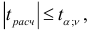 то гипотеза об отсутствии связи не вызывает возражении, т.е. принимается гипотеза
то гипотеза об отсутствии связи не вызывает возражении, т.е. принимается гипотеза 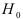 .
.
Значимость коэффициента корреляции можно определить, если воспользоваться критическими значениями коэффициента корреляции
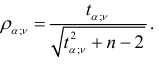
Существуют подробные таблицы критических значений коэффициента корреляции. При этом, если 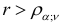 , то можно утверждать, что связь между переменными существенная; если же
, то можно утверждать, что связь между переменными существенная; если же 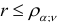 , то нет причин на основании выборки отклонить нулевую гипотезу об отсутствии связи.
, то нет причин на основании выборки отклонить нулевую гипотезу об отсутствии связи.
В случае, если при формулировке гипотезы 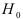 нельзя предположить, что коэффициент корреляции генеральной совокупности
нельзя предположить, что коэффициент корреляции генеральной совокупности 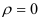 и, следовательно, нельзя положить
и, следовательно, нельзя положить 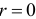 , применяют
, применяют 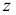 — преобразование Фишера
— преобразование Фишера
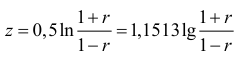
к статистике 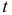 и получают статистику
и получают статистику
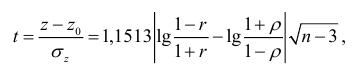
которая имеет 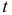 -распределение с
-распределение с 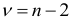 степенями свободы. Процедура проверки значимости проводится далее аналогично предыдущей.
степенями свободы. Процедура проверки значимости проводится далее аналогично предыдущей.
Иногда возникает необходимость проверки гипотезы об отличии друг от друга двух коэффициентов корреляции. При этом предполагается, что рассматриваются одни и те же признаки однородных совокупностей: данные представляют собой результаты независимых испытаний и применяются коэффициенты корреляции одного типа (коэффициенты парной или частной корреляции при исключении одинакового количества переменных). Объемы двух выборок могут быть различны. Нулевая гипотеза формируется в виде
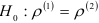
(коэффициенты корреляции двух рассматриваемых совокупностей равны). Альтернативная гипотеза 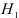 состоит в том, что
состоит в том, что
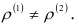
Для проверки нулевой гипотезы используется статистика
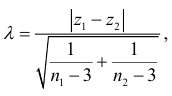
где 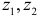 — значения
— значения 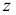 — преобразования Фишера коэффициентов корреляции
— преобразования Фишера коэффициентов корреляции 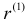 и
и 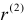 ;
; 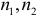 — объемы выборок.
— объемы выборок.
Если 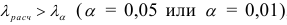 , то гипотеза
, то гипотеза 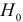 отвергается. В противном случае, т.е. при
отвергается. В противном случае, т.е. при  , гипотеза
, гипотеза 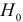 принимается. В случае принятия гипотезы
принимается. В случае принятия гипотезы 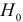 величина
величина
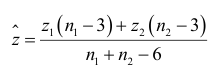
после преобразования
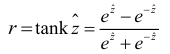
может служить оценкой коэффициента корреляции
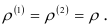
Затем проверяется гипотеза 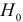 состоящая в том, что
состоящая в том, что 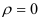 , с помощью статистики
, с помощью статистики
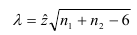
имеющей нормальное распределение.
Для проверки значимости коэффициента детерминации выдвигаются следующие гипотезы:
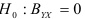 — переменная
— переменная 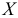 , включенная в регрессию, не оказывает существенного влияния на зависимую переменную
, включенная в регрессию, не оказывает существенного влияния на зависимую переменную 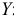 ;
;
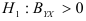 — переменная
— переменная 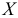 , включенная в регрессию, оказывает существенное влияние на зависимую переменную
, включенная в регрессию, оказывает существенное влияние на зависимую переменную 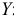 ;
;
В этом случае для проверки гипотезы следует использовать одностороннюю критическую область. Для оценки значимости парного коэффициента детерминации 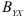 , используется статистика
, используется статистика
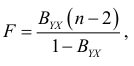
имеющая 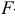 -распределение Фишера с
-распределение Фишера с 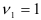 и
и 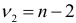 степенями свободы.
степенями свободы.
Значение статистики, вычисленное по результатам выборки, сравнивается с критическим значением 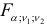 найденным по таблице
найденным по таблице 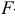 -распределения Фишера при заданном уровне значимости а и соответствующем числе степеней свободы. Если
-распределения Фишера при заданном уровне значимости а и соответствующем числе степеней свободы. Если 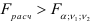 то вычисленный коэффициент парной детерминации значимо (с вероятностью 1 —
то вычисленный коэффициент парной детерминации значимо (с вероятностью 1 —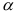 ) отличается от нуля и, следовательно, переменная
) отличается от нуля и, следовательно, переменная 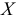 оказывает существенное влияние на переменную
оказывает существенное влияние на переменную 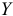 .
.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:
| Измерение интенсивности линейной корреляционной связи |
| Нелинейная регрессия и корреляция |
| Оценка адекватности регрессионной модели |
| Пример построения однофакторной регрессионной модели |

