Проверка статистической существенности (значимости) параметров множественной регрессии и показателей интенсивности корреляционной связи

Проверка статистической существенности (значимости) параметров множественной регрессии и показателей интенсивности корреляционной связи

Как отмечалось, каждый параметр корреляционно-регрессионного анализа является случайной величиной. Поэтому для ответа на вопрос, могут ли обнаруженные различия между оценками параметров корреляционно-регрессионного анализа и самими параметрами быть приписаны случайным колебаниям в выборке или они отражают существенное изменение условий взаимосвязи переменных, проводится проверка статистической значимости оценок на основе 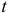— статистики.

Для проверки статистической значимости коэффициентов регрессии

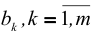, выдвигаются следующие гипотезы:

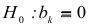— переменная 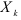не оказывает существенного влияния на зависимую переменную ;

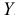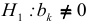— переменная 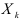оказывает существенное влияние на зависимую переменную .

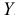Для проверки гипотезы 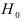используется статистика

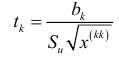
где 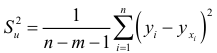дисперсия остатков; 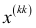— элемент главной диагонали матрицы 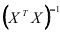. Статистика (2.16) имеет 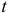-распределение Стьюдента с 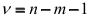степенями свободы. Если 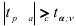, то с вероятностью 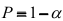нулевая гипотеза 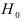отвергается, т.е. с вероятностью 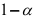можно утверждать, что переменная 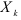оказывает значимое частное влияние на переменную 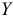. В противном случае, т.е. при 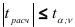, принимается гипотеза 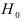. Следовательно, на основе данной выборки нельзя окончательно решить, значимо ли частное влияние переменной 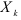на переменную .

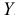Оценка статистической значимости парных коэффициентов корреляции проводится аналогично проверке гипотезы о статистической значимости выборочного коэффициента корреляции. Статистическая значимость коэффициентов частной корреляции проверяется также аналогичным способом, изменяется лишь число степеней свободы. Таким образом, для проверки гипотезы 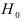, состоящей в том, что различие между выборочным частным коэффициентом корреляции и частным коэффициентом корреляции генеральной совокупности незначимо, вычисляется статистика

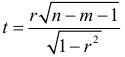
и сравнивается с критическим значением 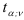, найденным по таблице 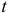-распределения при уровне значимости 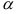и числе степеней свободы 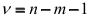. Принятие или отклонение гипотезы 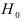проводится по правилу, которое описано в п. 1.8. Проверку значимости частного коэффициента корреляции можно осуществить, используя критические значения коэффициента корреляции и 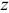-преобразование Фишера.

Оценка статистической значимости коэффициента множественной детерминации проводится с помощью статистики

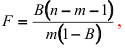
которая имеет 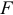-распределение с 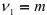и 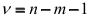степенями свободы. Расчетное значение статистики 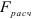сравнивается с критическим значением 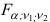, которое определяется по таблице 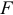-распределения при заданном уровне значимости 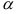и степенях свободы 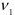и 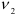. Если 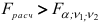, то вычисленный коэффициент детерминации значимо отличается от нуля. В противном случае, т.е. при 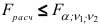, принимается нулевая гипотеза 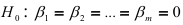, состоящая в том, что ни одна из переменных 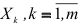, включенных в уравнение регрессии, не оказывает существенного влияния на зависимую переменную.

Для оценки существенности коэффициента частной детерминации применяется статистика

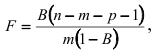
которая имеет 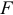-распределение с 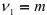и 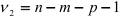степенями свободы. Здесь 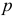— число переменных, исключенных при вычислении коэффициентов частной детерминации. Процедура проверки статистической значимости коэффициента частной детерминации аналогична процедуре проверки статистической значимости коэффициента множественной детерминации.

Так как между коэффициентами множественной корреляции и детерминации выполняется равенство

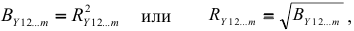
то о значимости коэффициента множественной корреляции судят по результату проверки значимости коэффициента множественной детерминации.

Кроме того, если 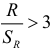, то с вероятностью 0,99 можно считать 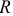статистически значимым.

Следует отметить, что дополнительное исследование изучаемой регрессионной модели может показать, что не все переменные, введенные в модель, имеют одинаковое значение в исследуемой регрессии. Поэтому, прежде чем вынести решение об исключении переменных из анализа вследствие их незначимого влияния на зависимую переменную, проводят исследование с помощью коэффициента детерминации. Для проверки предположения о включении в регрессионную модель переменных 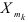можно применить критерий, который оценивает систематическое влияние дополнительно включенных переменных 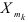. При этом рассматриваются две регрессионные модели:

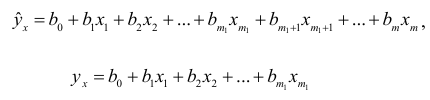
для которых 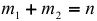, где 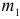— число переменных модели (2.18); 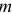— число переменных модели (2.17). В регрессии (2.17) по сравнению с (2.18) содержится дополнительно 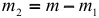переменных 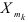. Для проверки гипотезы о том, вносят ли 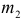переменных существенную долю в объяснение вариации переменной 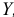, сформулируем гипотезу 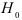, состоящую в том, что 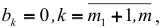, при альтернативной гипотезе .

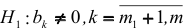Отметим, что влияние первых 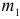переменных не оценивается. При проверке гипотезы 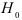используется статистика

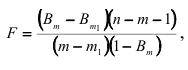
имеющая 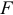-распределение с 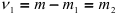и 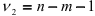степенями свободы. В формуле (2.19) 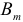— коэффициент детерминации регрессии с 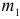переменными, a 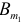— коэффициент детерминации регрессии с 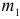переменными. Разность 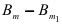в числителе формулы (2.19) является мерой дополнительного объяснения вариации переменной 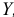за счет включения 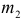переменных. Поэтому число степеней свободы числителя равно 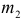. В критерии базой сравнения служит неопределенность функции регрессии с 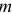переменными, поэтому число степеней свободы знаменателя равно 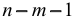. Если 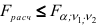то включенные дополнительно 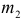переменные совместно неоказывают значимого влияния на переменную 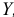. В противном случае, при 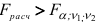гипотеза 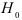на уровне значимости 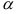отвергается, т.е. включенные 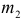переменные оказывают существенное влияние на вариацию переменной 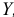. Критическое значение 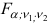находят по таблице 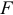-распределения при заданном уровне значимост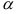и и 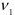, 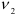степенях свободы.

Важной проблемой регрессионного анализа является сравнение оценок параметров регрессии. При этом выделяются две проблемы:

1) сравнение коэффициентов частной регресси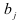и и 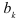одной и той же функции регрессии;

2) сравнение оценок параметров двух функций регрессии для двух различных выборок.

Для решения первой проблемы формулируем нулевую гипотезу 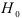, состоящую в том, что 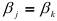, т.е. коэффициенты частной регрессии в генеральной совокупности равны. В альтернативной гипотезе 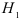предполагаем, что коэффициенты частной регрессии в генеральной совокупности значимо различаются. При этом если 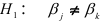, то используется двусторонняя критическая область, если же 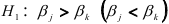то используется односторонняя критическая область. При проверке нулевой гипотезы 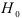может быть использован критерий

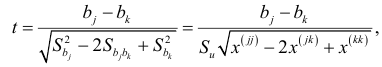
имеющий 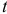-распределение с 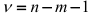степенями свободы. В формуле (2.20) 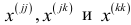— элементы матрицы 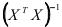. Решение о принятии гипотезы 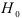принимается путем сравнения 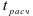с квантилем 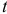-распределения для уровня значимост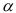и при 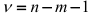степенях свободы. Если 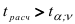, то гипотеза 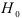с вероятностью а отвергается, т.е. коэффициенты регресси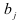и и 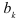статистически значимо различны. В противном случае гипотеза 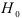принимается.

Сравним оценки параметров регрессии двух функций для двух выборок объемам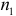и и 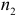. При этом предположим, что:

1) в обеих генеральных совокупностях исследуется содержательно одинаковая зависимость переменной Кот переменной ;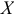

2) пары наблюдени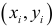й и 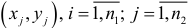, являются результатами двух независимых выборок объемам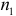и и 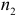из генеральных совокупностей;

3) по результатам каждой выборки строится простая линейная регрессия и находится дисперсия остатков:

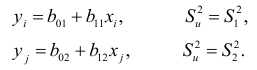
Для сравнения оценок параметров регрессий выдвигается нулевая гипотеза 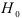, состоящая в том, что обе выборки произведены из генеральных совокупностей в среднем с одинаковой зависимостью переменной 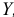от переменной 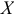: 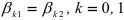. Альтернативная гипотеза 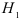заключается в том, что выборки произведены из генеральных совокупностей с разной зависимостью переменной .

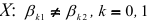Проверка гипотезы 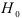разбивается на ряд этапов. На первом этапе выдвигается гипотеза 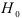, состоящая в том, что дисперсии остатков в обеих генеральных совокупностях равны, т.е. 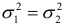против альтернативной гипотезы 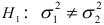. Проверка гипотезы 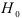осуществляется с помощью статистики

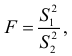
имеющей 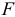— распределение при заданном уровне значимост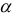и и 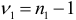, 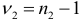степенях свободы. При этом в числителе стоит большая дисперсия. Если 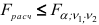то гипотеза 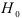принимается. В противном случае, т.е. при 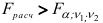, гипотеза 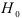отклоняется на уровне значимости 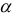. Если принимается 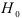, т.е. дисперсии остатков обеих генеральных совокупностей равны, то вычисляется сводная оценка дисперсии остатков 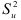для обеих регрессий:

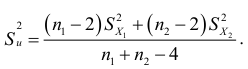
На втором этапе, после принятия гипотезы о равенстве дисперсий, выдвигается гипотеза 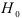, состоящая в том, что коэффициенты регрессии равны: 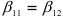против альтернативной гипотезы: 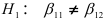Проверка гипотезы 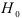осуществляется с помощью статистики

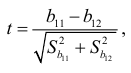
имеющей 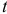-распределение с 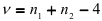степенями свободы. Подставив в статистику (2.22) оценки дисперсий коэффициентов регрессий и оценку дисперсии остатков (2.21), получим

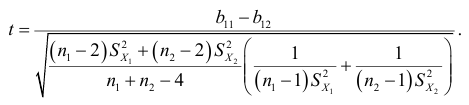
Из таблицы 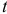-распределения для заданного уровня значимости 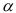и числа степеней свободы 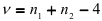определяем критическое значение 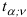. Тогда, если 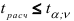, то гипотеза 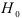принимается. Следовательно, различие между коэффициентами регрессии несущественно, т.е. регрессионные прямые параллельны. Уравнения регрессии могут различаться не угловыми коэффициентами, а своими постоянным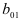и и 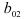. В противном случае, т.е. при 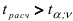гипотеза 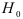отвергается. С вероятностью 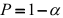можно утверждать, что регрессионные прямые не параллельны.

Если принимается гипотеза 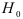, то вычисляется свободная оценка коэффициента регрессии по формуле

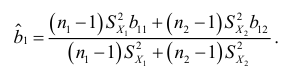
Если принимаются гипотезы о равенстве дисперсий остатков и коэффициентов регрессий, то оценивается расхождение свободных членов в двух сравниваемых уравнениях регрессии. Для этого выдвигается нулевая гипотеза 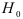, состоящая в том, что свободные члены 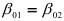против альтернативной гипотезы 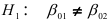. Проверку нулевой гипотезы 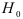осуществляем с помощью статистики

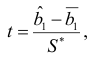
имеющей 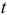-распределение с 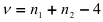степенями свободы. В статистике (2.24) 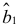— сводная оценка коэффициента регрессии (2.23), 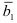— оценка углового коэффициента для двух уравнений регрессии, полученная по формуле

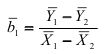
в предположении равенства как коэффициентов регрессии, так и свободных членов. Индекс в обозначениях средних соответствует номеру выборки. В формуле (2.24) стандартное отклонение

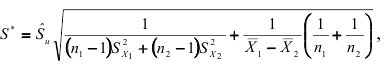
где 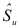определяется по формуле (2.21). Определив квантиль 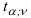для уровня значимости а при 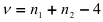степенях свободы, сравним его с 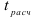найденным по формуле (3.24). Если 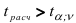, то постоянные регрессии существенно отличаются друг от друга на уровне значимости 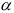. В этом случае прямые регрессии не идентичны, так как имеется статистически значимое расхождение постоянных. Если же 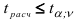, то обе регрессионные прямые считаются идентичными, а имеющиеся различия между ними можно объяснить лишь случайными колебаниями выборочных данных.

Таким образом, если на всех трех этапах принимаются нулевые гипотезы, то полученная форма усредненной зависимости может быть принята для обеих генеральных совокупностей.

Проверку гипотезы о совпадении уравнений регрессии для отдельных групп наблюдений (выборок) можно осуществить также при помощи теста Чоу, который состоит в следующем.

Пусть для двух выборок объемам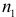и и 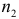построены два уравнения регрессии

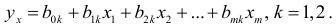
Проверим гипотезу 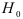, состоящую в том, что соответствующие коэффициенты регрессии равны:

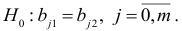
Обозначим 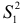и 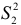дисперсии остатков для первого и второго уравнений регрессии. Пусть для объединенной выборки объема 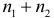построено еще одно уравнение регрессии, для которого дисперсия остатков равна 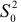. Для проверки гипотезы 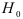применяется 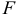-статистика:

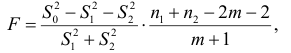
подчиняющаяся 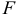-распределению с числом степеней свободы

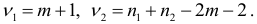
Тогда если 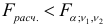то принимается гипотеза 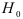. Это означает, что уравнения регрессии для обеих выборок практически одинаковы. Если же 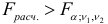, то нулевая гипотеза 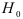отклоняется, что свидетельствует о различии уравнений регрессии с вероятностью .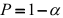