Оглавление:



Проверка прочности соприкасающихся тел
- Проверьте прочность корпуса на ощупь. Как уже указывалось в§ 35,материал контактного тела в центре контактной зоны находится в состоянии объемного напряжения и поэтому надежно работает при очень высоком напряжении сжатия. Чтобы проверить прочность материала в условиях объемного напряжения, необходимо знать величину главного напряжения в критической точке и создать условие прочности в соответствии с одной из следующих теорий:
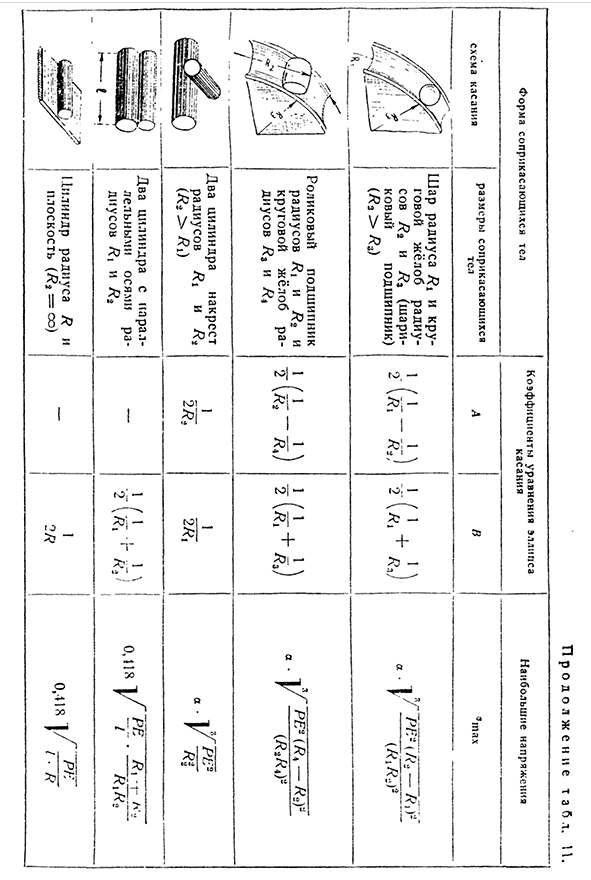
T ABL e I. уравнение коэффициентов L и amaV Контактная форма тела 1 Коэффициенты эллиптического уравнения и максимальное напряжение Контактная диаграмма размеры контактного тела Но В ’Макс’ С Два шара радиуса Ri и Ri Аль 4-а * 2 2А я#2 Р+Р3 2al Аль 0,3 С С / С} / П П<%+;’ Радиус шара A\и радиус шара сферы Т?2-А\РС-Ри 2асаи о д а]/р р р л■ » ЗЗ^ЗЗ^/^><^.^Zz>шар радиуса R и Плоскость (AA=OO) Один. 2Р Один. 2А 0.388 J т из re3- Но Радиус шарика Ri
и радиус цилиндра (H2>R1) Один. Г? Один. 1/Л+Ж3 2\7?Р ы ) ■В Ф Радиус Людмила Фирмаль
Al и А2 через радиус цилиндрической шаровой нет. > Эл) C-C-C }1 2A ’ i _и Ф ре’(Р3-Р) в (РИРВ)3 Вкладка контактное сопротивление п р О Д О Л ж е н и Е Л. П. Максимальный коэффициент контакта напряжение формы в уравнении эллипса контакта Контактная диаграмма размеры контактного тела Но В ’Макс’ 1 мяч в 7?I и радиус круговой канавки / / 7 ′ / ’ h7a / \g Sov T?2 и/или?3(Shari-1 1 21(2+f/PE-(r. RJ-F»K)подшипник) ) Г (А^)2 ibudn(П3>/?.) З’Г » Несущий (л/з^1′ ; Радиус f t и/?2 и круговое корыто РА-1 Два. М/Л<*/(клавиши F21(ж+ » львы ЛЕ2
((СДБ<р-т)) * р. г Миусов/?3, и/?4 два цилиндра 1 1 радиус 7?Я и/?2 нет. >З? Я) Черт возьми Параллельная ось RA1 dius и два цилиндра/?1 и/или? Два. ■Т — ; −1 Два.» (1. L-o, n»] / «■r ’ ^радиус цилиндра R 1 0 118 1’g плоскость (#2=co) 2/? У, у Г и Р Отчет О ЕС Ш-Б Три. ПЗ Ох ох ох С п о ПЗ ЗС Икс > О> • Три. Но г’— Х Х П-Н-м ’ −3 Багажник контактное напряжение sl156[глава IX Можно показать!) Опасная точка находится на определенной глубине контактного тела и по соответствующей формуле можно найти основное напряжение. Установлено, что
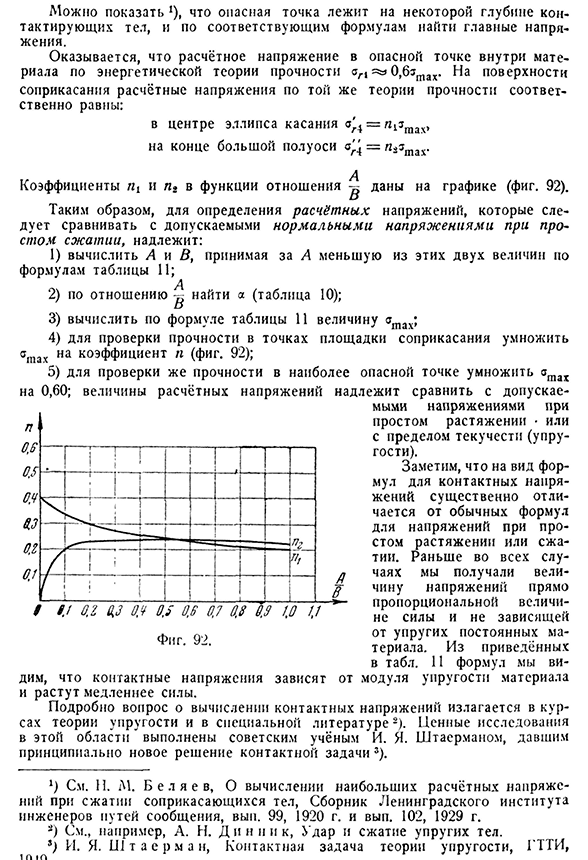
- напряжения, рассчитанные в критической точке внутри материала по энергетической теории прочности 0, BZT a x. на контактной поверхности напряжения, рассчитанные по той же теории прочности, равны соответственно: в центре контактного эллипса a’4=Y 13t a x, в конце большой полуоси<z’g’±=p2zt a x. Коэффициенты nt и P2 в функции отношения g приведены на графике(рис. 92). Поэтому для того, чтобы определить расчетные напряжения, подлежащие сравнению с нормальными напряжениями, допустимыми при простом сжатии, 1)вычислить а и В, и в соответствии с формулой
в таблице 11, эти 92); 5) испытать ту же прочность в наиболее опасной точке, умножить х на 0,60; величина расчетного напряжения должна быть сопоставлена с напряжением, в котором я не уверен. Отметим, что внешний вид формулы для контактного напряжения существенно отличается от обычной формулы для простого растяжения или напряжения при сжатии. Ранее во всех случаях она была прямо пропорциональна величине силы, а величина напряжения не зависела от упругой постоянной Q9mA-и g’teriala. Со стола. 11 уравнение мы находим, что контактное напряжение зависит от модуля упругости материала и растет медленнее,
чем сила. Задача расчета контактного напряжения подробно описана в курсе теории упругости и в специальной литературе * 2). Бесценные Людмила Фирмаль
исследования в этой области проводились советским ученым И. Это сделал я. 3) Штаерман, который дал принципиально новое решение контактной задачи. x) n. СМ. B E l I E V., в расчете максимального расчетного напряжения при сжатии континуума, сборник Ленинградского института инженеров железнодорожного транспорта, вып. 99, 1920 и т. 102, 1929 2) например, A. N. D и N. N. And K, см. удар и сжатие упругого тела.* ) И. Я. Ш т А Е Р М А Н, контактная задача теории упругости, ГТТИ, 1949,§ 46] проверка прочности контактного тела. Сто пятьдесят семь. П р и М Е р27 на г. Поставы. Вычислим радиус головки g=300lsm и результирующее напряжение на рельсах в точке соприкоснове
ния с фронтами локомотивного радиуса/? =470 мм; Нагрузка на рельс Р=7300 кг; модуль упругости стали Е=2 * 104 кг) мм2. «Мы имеем(согласно таблице 10 и): B= / J=0.64 и a=0.456. И так оно и есть., °Шах=0.456 г Е2=108вт/.Вт. У2; Расчетное напряжение в рельсах составляет og4=0.60 * 108=65 кг / мм2. На контактной поверхности расчетное напряжение составляет=0,24*(=26,0 кг) мм2. Где n=0,24 берется по графику (рис. 92)среднее между значениями рН и Р2. На контактной поверхности расчетное напряжение близко к пределу текучести, но внутреннее напряжение превышает его.
Смотрите также:
| Проверка прочности по различным теориям | Понятие 6 сдвиге. Расчёт заклёпок на перерезывание. |
| Общие понятия. Формулы для контактных напряжений | Проверка заклёпок на смятие и листов на разрыв |

