Простые и составные числа. Основная теорема арифметики
Натуральное число, большее 1, называется простым, если оно делится только на единицу и само себя и других натуральных делителей не имеет. Натуральные числа, большие единицы и не являющиеся простыми, называются составными. Например, число 17 простое, так как из натуральных чисел делится только на 1 и 17. А число 18 — составное, так как помимо 1 и 18 делится ещё, например, на 3. Вот несколько первых простых чисел, записанных в порядке возрастания:
2,3,5,7, 11, 13, 17, 19, 23,29,31,…
Число 2 — единственное чётное простое число, все остальные простые числа -нечётные.
Простых чисел бесконечно много, это было установлено ещё в древности (Евклид, III век до н. э.). Докажем этот факт методом «от противного». Предположим, что простых чисел — конечное число. Перенумеруем их в порядке возрастания: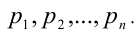 Рассмотрим натуральное число
Рассмотрим натуральное число 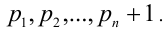 Оно больше каждого из простых чисел
Оно больше каждого из простых чисел 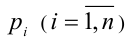 и делится на любое из них с остатком 1. Следовательно, это тоже простое число. Получили противоречие, которое означает, что сделанное предположение о конечности множества простых чисел было неверно.
и делится на любое из них с остатком 1. Следовательно, это тоже простое число. Получили противоречие, которое означает, что сделанное предположение о конечности множества простых чисел было неверно.
Заметим, что любое простое число, большее 3, может быть представлено в виде 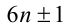 (обратное утверждение о том, что если число представимо в указанном виде, то оно простое, — неверно; докажите это самостоятельно).
(обратное утверждение о том, что если число представимо в указанном виде, то оно простое, — неверно; докажите это самостоятельно).
Эратосфен Киренский (ок. 276—194 гг. до н.э.) предложил для нахождения всех простых чисел, не превосходящих заданного натурального числа n > 1, метод вычёркивания из ряда натуральных чисел, меньших либо равных n , единицы и всех кратных последовательным простым числам 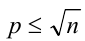 , кроме самих простых чисел. Этот метод получил название «решета Эратосфена». Восхищение вызывает француз Люка, доказавший в 1876 году (в эпоху, когда ещё не было компьютеров!) простоту числа, состоящего из 39 цифр:
, кроме самих простых чисел. Этот метод получил название «решета Эратосфена». Восхищение вызывает француз Люка, доказавший в 1876 году (в эпоху, когда ещё не было компьютеров!) простоту числа, состоящего из 39 цифр:
170141183460469231731687303715884105727.
Теорема (основная теорема арифметики). Каждое составное число разлагается в произведение нескольких простых чисел, не обязательно различных, причём такое разложение единственно с точностью до порядка сомножителей:
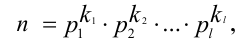
где п — составное число, о котором идёт речь в теореме, 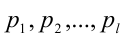 — различные простые числа,
— различные простые числа, 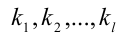 натуральные показатели степеней (без доказательства). Это разложение часто называют каноническим разложением числа на простые множители.
натуральные показатели степеней (без доказательства). Это разложение часто называют каноническим разложением числа на простые множители.
В задачах, где требуется выяснить, является или нет некоторое натуральное число п простым, обычно необходимо разложить исследуемое число п на множители, представив его в виде произведения как минимум двух целых чисел, и если все множители в полученном разложении отличны от ± 1, то делается вывод, что число п — составное.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

