Простые машины

Простые машины

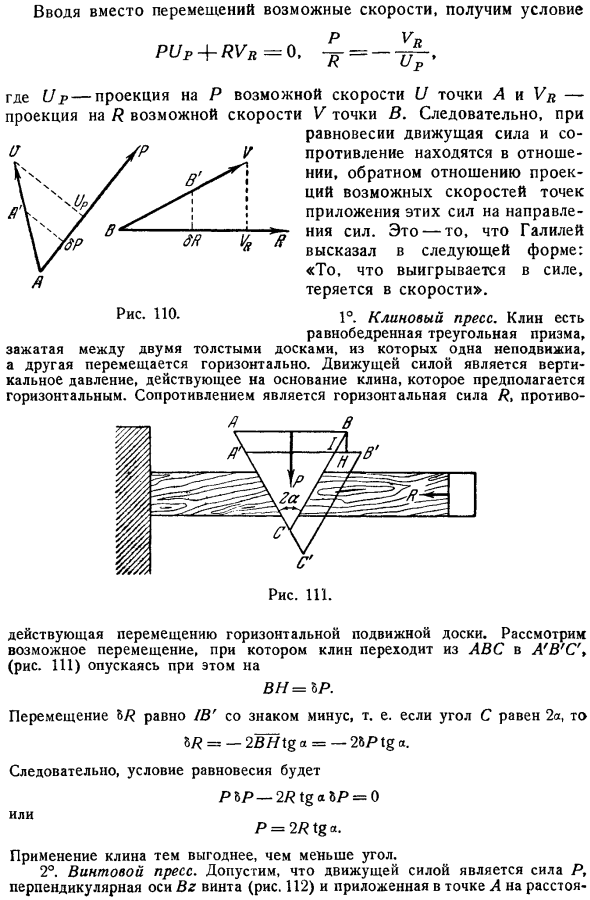
• Простая машина это полностью подключенная система. На машину действуют 2 силы. 1 Называется движущей силой, другой 1 называется R Resistance. To находя равновесное состояние, машина информируется только о бесконечно малых возможных перемещениях, допускаемых муфтой. При этом смещении P проецируется в направлении P смещения движущей силы точки A в направлении AA, а qR проецируется в направлении сопротивления точки B в направлении смещения BB в направлении R. Рисунок PO .Равновесное состояние переходит в возможное смещение вместо смещения. Получить условие пуп + РВР = вопрос. 4 = г Где Up проекция на P, а R возможная проекция Возможная скорость U точки A и Vr равна скорости V точки B. 

В равновесии движущая сила и сопротивление будут представлять собой обратное отношение проекции возможной скорости точек приложения этих сил в направлении действия силы. Это то, что он сказал в следующем что выигрывает теряет скорость. 1.Клиновой пресс. Клин представляет собой равнобедренную призму Он зажат между 2 толстыми досками, одна закреплена, а другая движется горизонтально. Движущей силой является вертикальное давление, действующее на основание клина, которое предполагается горизонтальным. Сопротивление это горизонтальная сила Rt Галилей формат: включена Переместите горизонтальную подвижную пластину, чтобы действовать. Рассмотрим возможное смещение клина от ABC до a b c 9 рис. 

Эти условия очень просто выражаются при помощи следующего построения, приводящего к многоугольнику Вариньона. Людмила Фирмаль

Смещение bR равно B со знаком минус, то есть если угол C равен 2a, то bR = 2BH g a = 26P tg a. В результате состояние равновесия выглядит следующим образом ПБП тг 2Р и 6р = о Или Р = 2Р тг собой. Использование клиньев выгодно, чем меньше угол. 2.Винтовой пресс. Предположим, что движущей силой является сила P рис.112, перпендикулярная оси винта Bz, приложенная в точке A расстояния a, перпендикулярного плоскости AzB от этой оси, и сопротивление R, действующее вдоль самой оси. Бесконечно малое вращение 5 проекция дуги спирали, которая описывается точкой а, в единственном движении, допускаемом соединением, на Р это дуга радиуса а центрального угла 60.

Очень важный = 86 Где h шаг винта. Движение винта вдоль оси пропорционально его вращению, а шаг h величина этого движения при полном вращении винта. Форма равновесного состояния является PaB R. 80 = 0 Из этого видно, что выгодно увеличить расстояние рис U2. уменьшить шаг винта. 3.Квинтэссенция. Весы состоят из коромысла ABC рис. 113, которое вращается вокруг точки O и поддерживает 2 горизонтальные платформы с помощью шарнирно соединенных стержней BB и CC к нему Рисунок 113.

Утяжеленное тело помещено на верхней платформе и сбалансировано весом P суспендировать на пункте A так, что коромысло ABC будет горизонтально. Поверните 60 коромысла бесконечно мало вокруг оси, очевидно ZP = OA 60. Что касается перемещения 6P, то оно зависит от положения груза на платформе FB. Если только платформа не движется параллельно самой себе, то есть если точки F и B не увеличиваются на одну и ту же величину. Заметим, что для представления этого состояния точка B поднимается на ту же величину, что и B, то есть на 60 об. Точка с увеличивается на 60 оС, а точка С на столько же.

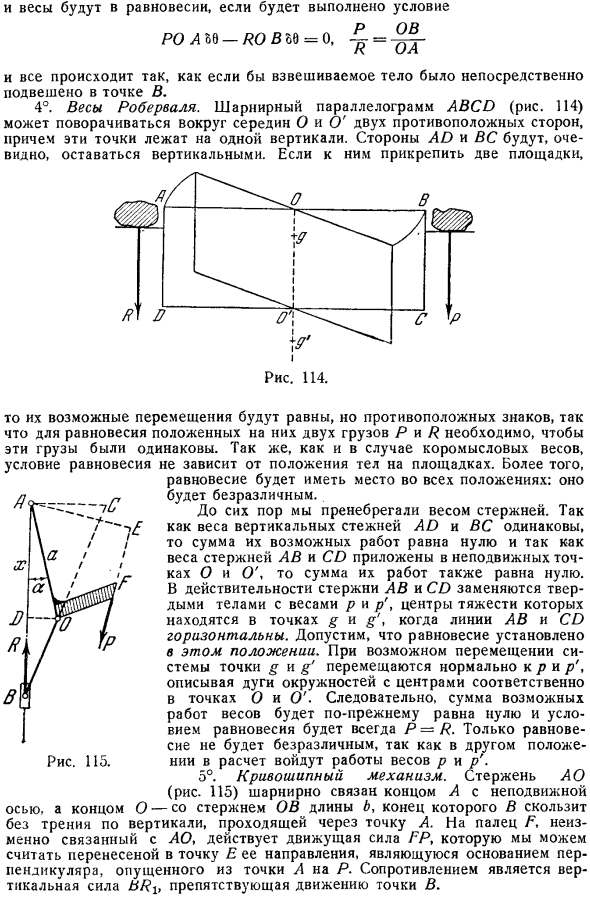
Точка F поднимается до OS 60. Поэтому желательным состоянием является С Ребенок следующим образом Если ОБИ ОС. ЕСЛИ ОБЬ ОС Линии 01 и BF пересекают CC .С этим Предположения у нас есть Если ZR = OB 60 и условие 56 выполнено, то баланс будет находиться в равновесии so = o, = А дальше все происходит так, как будто измеренное тело подвешено прямо в точке Б 4.Весы ровал это. Шарнирный параллелограмм ABCD рис.114 может вращаться вокруг 2 противоположных средних точек O и O , причем эти точки находятся на одной вертикали. Стороны AD и BC остаются четко вертикальными.

Когда установлены 2 колодки В этом случае возможные перемещения будут равны, но так как знак будет противоположным, то для баланса 2 х нагрузок Р и Р, размещенных на них, эти нагрузки должны быть одинаковыми. same. As в случае балансировочных грузов состояние равновесия не зависит от положения объекта на поверхности. site. In кроме того, равновесие возникает во всех положениях. Будет безразлично. До сих пор вес стержня игнорировался.

Вес вертикальных стержней AD и BC одинаков, поэтому сумма возможных заданий равна нулю, а веса стержней AB и CD применяются в фиксированных точках O и O , поэтому сумма заданий также равна zero. In фактически стержни AB и CD заменяются твердым телом с весом p и p , где центроид находится в точках g и g , Когда линии AB и CD горизонтальны. Предположим, что в этом положении устанавливается равновесие. Из за возможного движения системы точки g и g обычно перемещаются в p и p , представляя собой дугу окружности с центром в точках O и O , respectively. As в результате суммарная возможная работа шкалы все равно будет равна нулю, а состояние равновесия всегда будет P R.

Только равновесие не безразлично, так как в другом положении работа шкал p и p включается в расчеты. 5.Кривошипный механизм. Стержень АО рис. 115 поворачивается к стержню длиной b OB к неподвижному O концом A. Ось, а конец О имеет стержень oo длины o, и его конец скользит без трения, проходя через точку A перпендикулярно. На палец F, который всегда связан с АО, действует движущая сила PP, которая, как предполагается, передается в точку. Сопротивление это вертикальная сила BRlt, которая блокирует движение точки B. единственное движение, допускаемое соединением, является результатом поворота стержня АО на 1 угол. При таком смещении работа силы P равна РПР = раеьа.

• Задача сопротивления R bx. Где X расстояние Ab. Треугольник АОВ 4 2ax потому что И с дифференциацией мы получаем О = Х ВХ а потому что ВХ 4 Син Син ба, откуда ну грех а о.= бакалавр искусств х потому что Таким образом, состояние равновесия является п р ах грех а АЭ х хорошо живется в Нарисуйте OD и AC перпендикулярно AB, а точку в C Пересечение последнего перпендикуляра и продолжения линии VO.

У нас есть ОД = грех, ВD = х а потому что, = 4 = БД ОО Условие равновесия описывается в простой форме: Спикер P xod Ах. AEBD 6.Поли паста 2 блочных систем, в которых общая клетка или блок прикреплены к общей оси или к отдельной оси. Первая система остается неподвижной, а вторая движется рис.116.Предположим, что каждая система состоит из 3 блоков. Первый блок это блок, В, С, и 2 от Блока АВ на АВ. В фиксированной точке B первой системе клип, веревка фиксируется, А1а, а ag, …Движущей силой Р является напряжение, действующее на свободный конец троса. Сопротивление R это нагрузка, подвешенная в нижней части подвижной системы. Между 2 системами блоков 6 частей частей, ГХ…… Параллельный.

Рассмотрим веревочный многоугольник, находящийся в равновесии под действием сил, приложенных к его различным вершинам. Людмила Фирмаль

Общая длина нити равна L1..1 это не одно и то же. Если вы переместите свободный конец нити на 6P, каждая часть, окруженная 2 блочными системами, будет сокращена на P. Это выражение является значением br, с противоположным знаком, и находится в равновесии. Подъем. Каждый из них Полиспаст крепится Веревку я заключаю можно считать па 1 = я Р 7. Неэластичная цепь скользит без трения по фиксированной кривой.

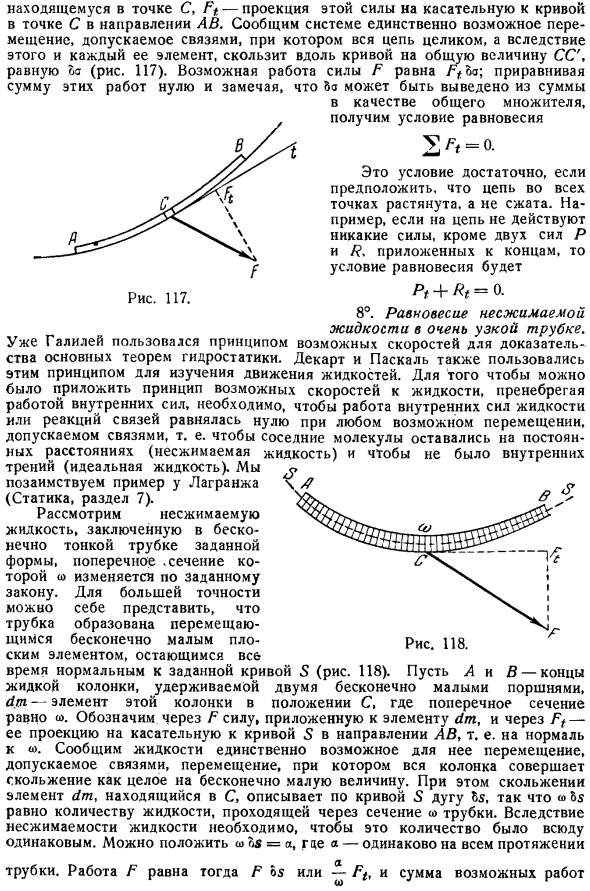
Предположим, что A и B концы цепи и их толщина бесконечно мала, F сила, приложенная непосредственно к элементу dst в точке C, Ft проекция этой силы на касательную кривой в точке C в направлении C. информирует систему о единственно возможных движениях, которые допускаются соединением. Всю цепочку, и, следовательно, каждый из его элементов, скользит по кривой с суммой УК, равный да рис. 117.Возможные задания сумма этих заданий равна нулю Когда вы воете при общем значении SS, сила F равна Ffcxj.

Уравнение с Да может быть оценено из суммы как общий фактор, и получено равновесное состояние 2 F = 0. Если предположить, что цепь не сжимается во всех точках, а растягивается, то этого условия достаточно. Например, если на цепь не действует никакая сила, за исключением того, что на обоих концах приложены 2 силы P и R, то состояние равновесия равно: П 4 Е = 0. 8.Равновесие несжимаемой жидкости в очень тонкой трубке. Возможная скорость для сертификации Что Рисунок 117. Уведомление Основа Если быть более точным Галилей уже использовал основную теорему гидростатической механики.

Декарт и Паскаль также использовали этот принцип для изучения движения liquids. To примените принцип возможной скорости к жидкости и игнорируйте работу внутренних сил, работа внутренних сил жидкости или реакция сцепления должны быть равны нулю для любого движения, сделанного возможным благодаря сцеплению, то есть соседние молекулы остаются на определенном расстоянии так, чтобы не было внутреннего трения, которое является идеальной жидкостью. Позаимствуйте пример из Лагранжа статика, Раздел 7. Рассмотрим несжимаемую жидкость, окруженную бесконечно тонкими трубками заданной формы, поперечное сечение которых изменяется по заданному закону.

Трубка может быть образована подвижным элементом, который остается перпендикулярным заданной кривой S рис.118. Пусть жидкий столб, удерживаемый бесконечно малыми числами A и 2 dm, является элементом положения C этого столба. Где горизонтальная ось равна o. Он показывает силу, приложенную к элементу dm в F, а в Ft проекцию направления AB, то есть касательную кривой 5 к нормали. Позволенный соединением, которое говорит жидкости только возможное движение, все движение колонки смещает инфинитно как a whole. In это скольжение, элемент dm в C представляет собой дугу ds вдоль кривой S, поэтому 5s равно количеству жидкости, проходящей через участок трубки.

Из за несжимаемости жидкости это количество должно быть одинаковым везде. w ds = a, gee a может сделать то же самое для всей трубки. Задание F это F os или Ft, сумма возможных заданий Совсем маленький BC6 B концы в поршне, поперечное сечение силы, приложенной непосредственно, равно a таким образом У меня достаточно равновесия. Предположим, что столбец сжат во всех точках.

Например, если сила, приложенная к жидкости, является только вертикальным давлением Po и Pt, приложенным к поршням A и B в сечении o0, равновесное состояние будет: Ох = о. В0 0 Л Заметим, что для равновесия жидкости то же самое уравнение может быть достигнуто при следующих условиях: представим себе закрытый контейнер любой формы. Оттуда создаются секции a 0 и j 2 цилиндрические трубы A и B. Предположим, что сосуд заполнен жидкостью, на жидкость не действует сила, приложенная непосредственно, а трубка закрыта 2 поршнями А и в, которые подвергаются обычному давлению Po и Px.

Если поршень а движется на бесконечно малую величину e0, то внутренний объем уменьшается на e0co0.Таким образом, поршень B должен подняться на величину e, например 0 o0 существует уравнение равновесия, поскольку сумма возможных работ Po и Px очевидно равна Po0. 0 Ле = 0, по Т = 0.

Смотрите также:

Решение задач по теоретической механике

Лемма	Основное уравнение статики
Системы с полными связями	Приведение уравнений равновесия к наименьшему числу