Оглавление:


Простые и сложные проценты
Простой и сложный процент. <5 (0 = 7 ^ 7-0 <4 <1 <^ 2. (3.1) В случае 1 + zt выражение (1.5) в интервале [0, 1] равно u (0 = l + rt, 0 <*) <1.
- Таким образом, сила (3.1) точно характеризует простой случай процентов для годовой процентной ставки i: простую схему начисления процентов для годовой процентной ставки i
и постоянную процентную ставку 6 (t) = 6, соответствующую годовой процентной ставке i. Людмила Фирмаль
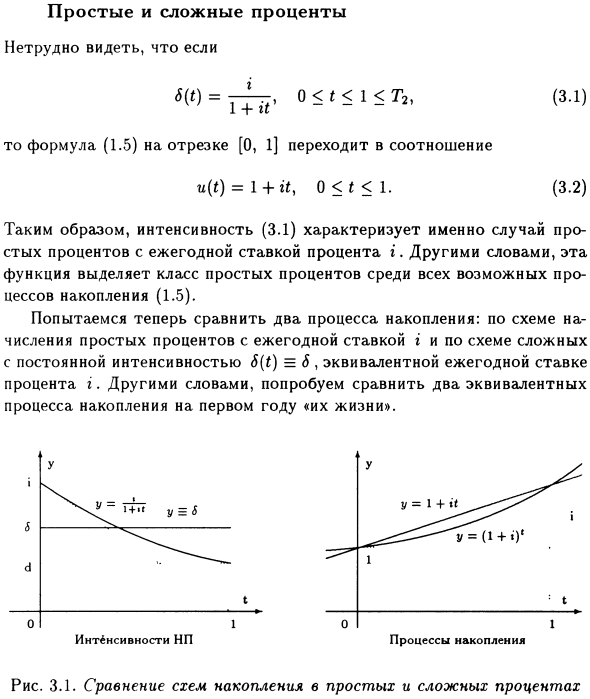
Другими словами, мы пытаемся сравнить два эквивалентных процесса накопления в первый год «их жизни» Рисунок 3.1: Сравнение простых и сложных схем накопления скорости На рисунке 3.1
В упражнении 5 предлагается математически подтвердить этот вывод.Кроме того, в некотором смысле наиболее выгодным моментом блока питания является то, что функция y = (14- 🙂 *;
- Пример 3.1: Запишите уравнение для точки PSU в = = (i) 3.1 принимает максимальное значение, указывая, что значение to для малого i составляет около 1/2, а в ( 0,1) Определить решение 1.
Значение 1 Точка, в которой 4-it ~ (1 4-i) * достигает своего максимума,
является решением уравнения (14-t) * ln (14-i) = r, Людмила Фирмаль
поэтому = [1п (: / 5)] / 5. 2. Используя известные соотношения (14-z) ~ x, x-> 0 и (II.2.17), 1, z, r! -D i-6 1. R0 = jln ( l + -y-) ~ — ^ — ~ -, r- * ° -3. В ПД.1 6 = 0,09531, поэтому (0,1) = 1р (0,1 / 0,09531) / 0,09531 = В (1,04920 ) /0.09531 = 0.5036 •
Рисунок 3.1 (слева) указывает, что функция y = 1 4-it на интервале (0,1) более выгодна для кредитора, поскольку функция y = (14-i) 1 выше
Вышеуказанные факты четко объяснены: начало интервала (0, 1) интенсивности (3.1) выше, чем постоянная интенсивность y = 6, и к концу ситуации ситуация меняется на противоположную.
Это только указывает на реальную власть, и в реальной жизни интервал, в котором используется простой интерес, ограничен одним годом.
В случае целесообразно добавить, что использование сложных процентов составляет почти 100%, но, конечно, это происходит, когда они используются в транзакциях менее года.
Часто используется в краткосрочных операциях. Длится меньше года. Однако у них есть другие области применения.
Это связано с тем, что при использовании периодических ставок в финансовых операциях за период (связанный с рассматриваемым периодом) формула сложного процента не дает достаточного описания изменения стоимости денежной единицы с течением времени.
Следовательно, требуется упрощенное приближение, часто опирающееся на простые пропорции.
Смотрите также:
| Функции накопления, эквивалентные данной ставке. | Простой дисконт. |
| Простые проценты и простой дисконт. | Простой и сложный дисконт. |

