Простейшие свойства функции Г

Оглавление:

Простейшие свойства функции Г

Функция G. простейшие характеристики 1°. Функция G (a) непрерывна для всех значений a^>0 и имеет непрерывные производные всех порядков. Достаточно доказать только S S S t V o V i

p R o I V O d n s x. дифференцируя Интеграл(6) под знаком интеграла、 0, 0. (7.) Применение правила Лейбница заключается в том, что оба интеграла являются 1ОО Отчет (мажорант x a°-1 / 1P x|)x-OA для X-OA для X-OA для X-OA для X-OA для X-OA для X-OA (мажорант x A e-x*)

x-oa для x-1 для X-OA для X-OA для X-OA для X-OA *) Если X>0, то, очевидно, Людмила Фирмаль

1n x) 311]§4. Интеграл Эйлера 171 2°. (6) от, путем интегрировать части, мы получим вас быстро: А×0″1е-×ух=×а+о ^х е~х-ых, То есть Г(а — {-1)=а-г(а). Эта формула применяется повторно, давая G(a+p)=(a+p-1)-(a+p-2). . . . . (а+1). АГ(а). (8) (8) Таким образом, вычисление G для любого значения в аргументе a можно свести к вычислению G Для(или 1 и 2,

Если хотите). Возьмите If в(8)=\и примите это во внимание И Г(1)=^е-х х=1,(9) О Это Г(п+1)=п! (10) таким образом, функция G является естественным расширением области положительных значений l y b y x функции аргумента N\ и определяется только для естественного значения пункта 3 формулы изобретения. Здесь мы можем

составить общее представление о поведении функции G (a) при увеличении a от 0 до OO. Из (9) и(10) мы имеем: G (1)=G (2)=1, согласно теореме о роли, между 1 и 2 должен быть корень A0 производной G0(a). Эта производная постоянно увеличивается, а вторая производная G»(a), Как видно из ее формулы (7), всегда положительна. Таким образом, в 0<^a<^A0 производная G^X O,функция G (a)уменьшается, и A0<^a<^OO становится G'(a)^>0, поэтому G(a) увеличивается.a = A0 имеет минимальное значение. Расчет, который

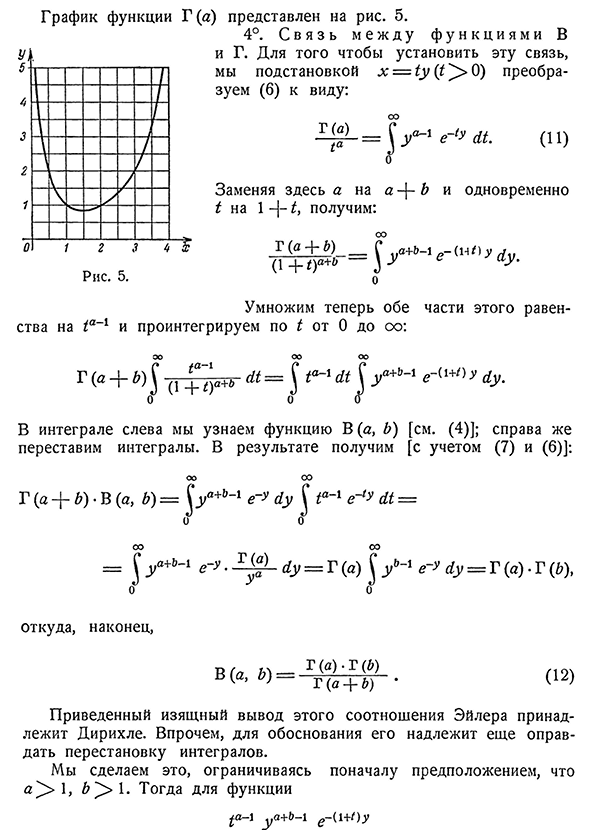
мы не даем, дает A0=1.4616…Пип G(А)=Г(значения i0)=0.8856… Интересно установить еще один предел для G (a), когда A близок к 0, А II к OO. Из(8) (и из 1°) ясно, что ООО С другой стороны, в терминах (10), G (a)^>и! только a^>p- / -1, т. е. G (a)—{- OO и a--| — OO.172 зависит от параметра chap XVIII. интегралы[311 График функции g(a)показан на рисунке. 5. 4°. Чтобы установить это соединение, подставьте x=6U для преобразования (1) в следующий вид: ООО Е М (11) Здесь замените a на B и в то же время замените I на 1~ / — мы получим: Г(Д+^) — хорошо (у+1)А+Б-уу е АУ’ Отчет Умножьте обе части этого уравнения

на 1A — ^и интегрируйте с I от 0 до OO: Г(А+Б)С М==Г Г я^+B_1g_(1+/)г г г ю- Людмила Фирмаль

Примерно от 0 до 0 Левый Интеграл распознает функцию B (a, B) [см.(4)]. В результате [рассмотрим (7) и (6)]: G (a+B)•B (a, B)=G y+»-1e-Y Y1 1A-1e-1U-1U A1=O Отчет у=Г е н ю!г=г(а)•г(/>), Окончательно, В(А,Б) Г(а) г(&)г(а+)'(12) Приведенный выше изящный вывод этого отношения Эйлера принадлежит Дирихле. Но чтобы обосновать это, необходимо обосновать перестановку интеграла. Мы делаем это, ограничившись предположением, что a^>1,1 сначала. Тогда функция^■a-1ua+B-1e~(1+() U311]§4. Интеграл Эйлера 173 Выполнены все условия теоремы 5n°305:

эта функция n e N R e r s n a (и даже положительная) y^O и 1^0, а также Интеграл ООО Ноль. г,+Б-1д-г^е-1У<#=Г (А)Г Б~*Е~Г Отчет От первого-1^0, от второго-y до y^O. ссылка на теорему обосновывает перестановку интеграла, используя ее в случае формулы (12) — a^>1,6^>1. Если известны только a^>0 и 6^>0, то доказано-B (a+1, 6 4-1)=G (a+1) G (6+1) T (a+d+2）) И отсюда легко использовать (2), (2′) для функции B, (8) для функции G, чтобы снова получить выражение (12) без лишних ограничений. 5°. Если вы введете в Формулу (12) 6=1-a

(count 0<^a<^1), рассмотрим (5) и (9)、 G (a) G(1 — «) = —^— , (13) Это называется Ф О Р М У Л О й д О П О Л Н Е Н И. A= — ^ — найти его отсюда(G (a)^>0): Путем выполнения в Интеграле ООО О Г Заменяя g=x2, мы снова получаем уже известный нам Интеграл O174 XVIII.Интеграл, зависящий от параметров(311 6°. Ф О Р М У Л А Л еж Ан д р а. Для целых чисел Произвести замену Тогда мы получаем Один. 22Я-1 В обоих случаях замените функцию в этом выражении (12) на G: Г (О)Т («) _1G(2′)г<11) Г (2»>2 -+ Если уменьшить G (a) и присвоить ему значение[см.(14)], то f o R m u l e L Ezh an d R a:G(a) G(a) G (A=G(2A)). Существует множество других формул, раскрывающих глубинную

природу функции G. Здесь также есть возможность остановиться не только на методе приближенного вычисления значений функции g и ее логарифмов, но и на них, используя аппарат свойств функции G и бесконечного ряда, сначала составляя таблицы дробного логарифма G (a) от 1 до 2 до 0,001, а затем 7, а затем 12. Новая, уже не элементарная функция G освоена нами в той же мере, в какой мы хорошо знаем функции, которые мы называем элементарными.

Эйлеров интеграл первого рода	Исторические замечания о перестановке двух предельных операций
Эйлеров интеграл второго рода	Понятие неявной функции от одной переменной.