Простейшие тригонометрические уравнения примеры с решением

Простейшие тригонометрические уравнения. Уравнения, сводящиеся к алгебраическим относительно sin x, cos и tg x

Справочные сведения

1. Решение тригонометрических уравнений сводится в конечном итоге к решению простейших тригонометрических уравнений, т. е. уравнений вида

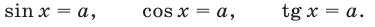
а) Если 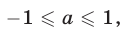то все корни уравнения

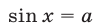
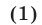
определяются формулой

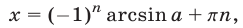
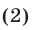
а все корни уравнения

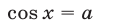
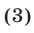
— формулой

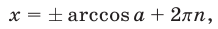
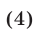
где 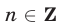( 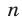принимает любые целые значения).

Если 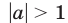, то уравнения (1) и (3) не имеют корней.

б) Уравнение

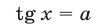
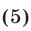
при любом а имеет корни, определяемые формулой

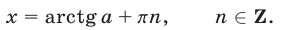
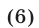
в) Формулы нахождения корней некоторых часто встречающихся простейших тригонометрических уравнений:

Рассмотрим уравнение вида

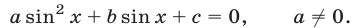
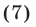
Полагая 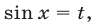, перепишем уравнение (7) в виде

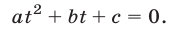
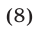
Пусть 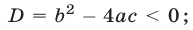тогда уравнение (8) не имеет действительных корней и поэтому уравнение (7) также не имеет корней. Пусть 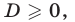тогда уравнение (8) имеет корни

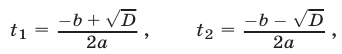
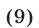
а уравнение (7) равносильно совокупности уравнений

Уравнение (7) имеет корни тогда и только тогда, когда 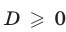и по крайней мере одно из чисел 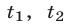по абсолютной величине не превосходит единицы, причем:

а) если 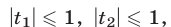то уравнение (7) имеет две серии корней

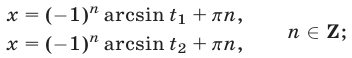
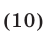
б) ес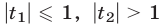ли или 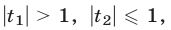то уравнение (7) имеет одну серию корней, определяемую первой или второй из формул (10) соответственно.

К квадратному уравнению можно свести уравнение

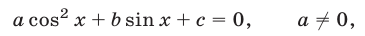
если заменить 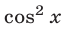на 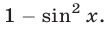Аналогично, уравнения вида

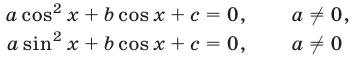
также приводятся к квадратным уравнениям. Рассмотрим уравнение вида

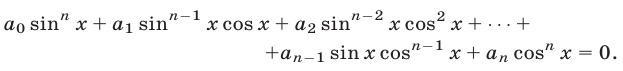
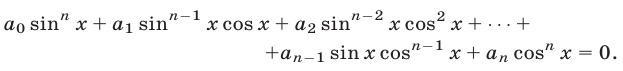
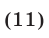
В каждом слагаемом левой части уравнения (11) сумма степеней синуса и косинуса одна и та же и равна 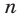. Такое уравнение называется однородным относительно 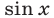и а число 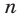— показателем однородности.

Рассмотрим однородные уравнения с показателями 1 и 2, т. е. уравнения вида

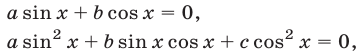
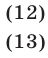
предполагая, что в уравнении (12) хотя бы одно из чисел 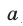, 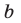не равно нулю, а в уравнении (13) хотя бы одно из чисел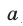, , 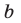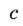отлично от нуля.

Пусть в уравнении (12) 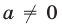; тогда значения 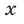, при которых 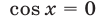, не удовлетворяют уравнению (12), так как если 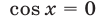, то 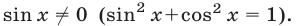Поэтому в случае 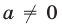, разделив обе части уравнения (12) на 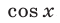, получим равносильное уравнение

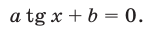
Аналогично, если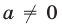, то разделив обе части уравнения (13) на 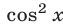, получим равносильное уравнение

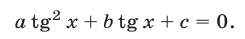
Примеры с решениями

Пример №107.

Решить уравнение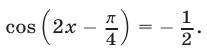

Решение:

По формуле (4) находим 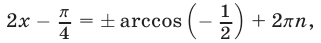где 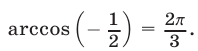Отсюда следует, что

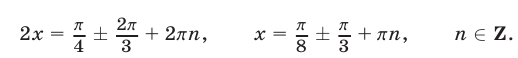
Пример №108.

Решить уравнение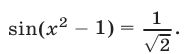

Решение:

Согласно формуле (2) получаем

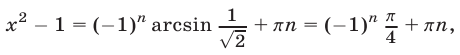
откуда 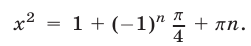Так как правая часть этого равенства должна быть неотрицательной, то 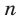может принимать только значения 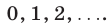Отсюда находим

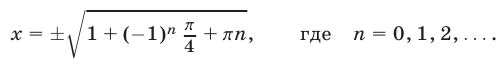
Пример №109.

Решить уравнение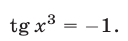

Решение:

Применяя формулу (6), находим

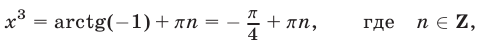
откуда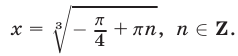

Пример №110.

Решить уравнение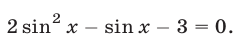

Решение:

При 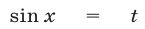получим квадратное уравнение 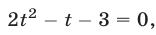имеющее корни 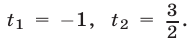Так как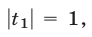 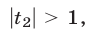то исходное уравнение равносильно уравнению 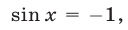откуда находим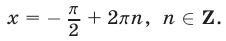

Ответ.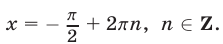

Пример №111.

Решить уравнение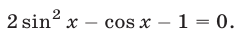

Решение:

Пусть 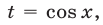тогда 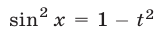и уравнение примет вид

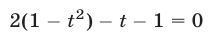
или

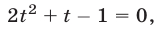
откуда находим 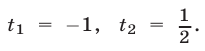Если то 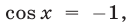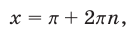а если 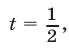то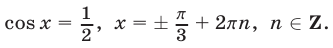

Ответ.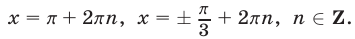

Пример №112.

Решить уравнение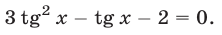

Решение:

Полагая 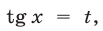получаем уравнение 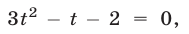имеющее корни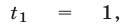 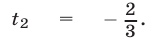Исходное уравнение равносильно совокупности уравнений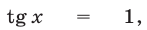 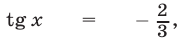откуда находим две серии корней:

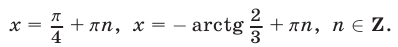
Пример №113.

Решить уравнение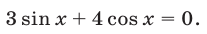

Решение:

Данное уравнение равносильно каждому из уравнений 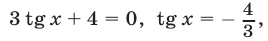откуда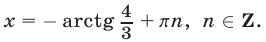

Пример №114.

Решить уравнение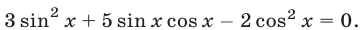

Решение:

Разделив обе части уравнения на 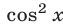, получим равносильное уравнение 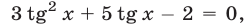имеющее корни 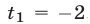, 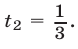Исходное уравнение, равносильное совокупности уравнени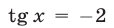й и 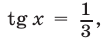имеет две серии корней: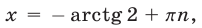

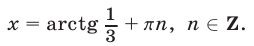
Замечание. К уравнению вида (13) сводится уравнение

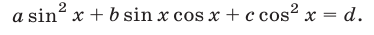
Для этого достаточно воспользоваться тождеством

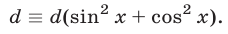
Пример №115.

Решить уравнение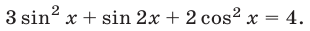

Решение:

Это уравнение равносильно каждому из следующих уравнений :

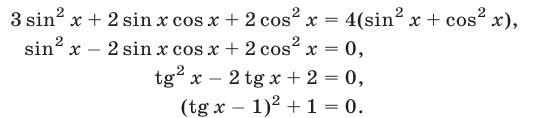
Значит, исходное уравнение не имеет корней.

Пример №116.

Решить уравнение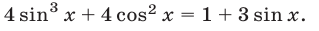

Решение:

Полагая 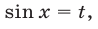преобразуем уравнение к виду

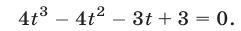
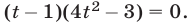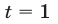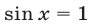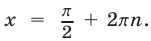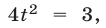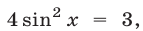
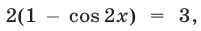
Разложив левую часть полученного уравнения на множители, приходим к уравнению Если , то , откуда Если то 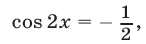откуда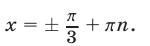

Ответ.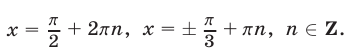

Пример №117.

Решить уравнение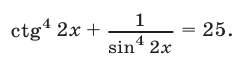

Решение:

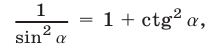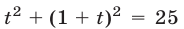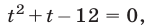Полагая и используя формулу преобразуем уравнение к виду или откуда 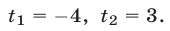Следовательно, 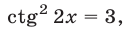откуда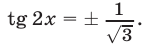

Ответ.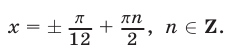

Пример №118.

Решить уравнение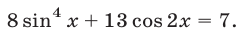

Решение:

Полагая и используя формулу 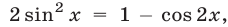получаем уравнение 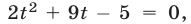имеющее корни 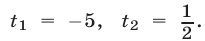Следовательно, 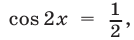откуда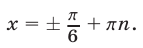

Ответ.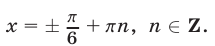

Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:

Решение задач по математике

Возможно вам будут полезны эти страницы:

Показательные уравнения примеры с решением

Логарифмические уравнения примеры с решением

Решение уравнений с помощью введения вспомогательного угла, методом замены неизвестного и разложения на множители, с помощью формул понижения степени примеры с решением

Уравнения, решаемые с помощью оценки их левой и правой частей с примерами решения