Оглавление:
Рассмотрим дифференциальные уравнения первого порядка.
Уравнения вида 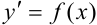 назовем простейшими диф. уравнениями первого порядка.
назовем простейшими диф. уравнениями первого порядка.
Например, уравнения 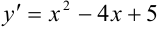 ,
, 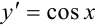 — простейшие дифференциальные уравнения первого порядка. Обращаем внимание, что в левой части уравнения находится только
— простейшие дифференциальные уравнения первого порядка. Обращаем внимание, что в левой части уравнения находится только 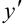 , а в правой — выражение, содержащее только переменную
, а в правой — выражение, содержащее только переменную 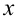 .
.
Для решения простейших дифференциальных уравнений первого порядка достаточно взять интеграл от правой и левой части по переменной 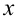 :
: 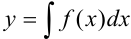 .
.
Пример №38.2.
Найдите решение дифференциального уравнения 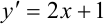 .
.
Решение:
Поскольку перед нами простейшее дифференциальное уравнение первого порядка, найдем его решение по формуле 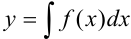 :
:
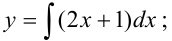
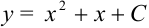 — общее решение дифференциального уравнения
— общее решение дифференциального уравнения 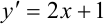 .
.
Ответ: 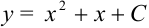 .
.
Пример №38.3.
Найдите решение задачи Коши: 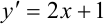 , если
, если 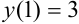 .
.
Решение:
Общее решение заданного дифференциального уравнения имеет вид: 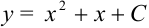 (см. пример 38.2) . Воспользуемся начальными условиями:
(см. пример 38.2) . Воспользуемся начальными условиями: 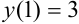 , следовательно, при
, следовательно, при 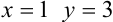 . Подставим эти числа в общее решение:
. Подставим эти числа в общее решение:
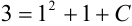 . Выразим из данного уравнения
. Выразим из данного уравнения 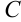 :
: 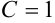 .
.
Подставив найденное значение 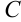 в общее решение
в общее решение 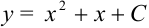 , получим следующее частное решение дифференциального уравнения:
, получим следующее частное решение дифференциального уравнения: 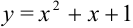 .
.
Ответ: 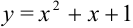 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:

