Оглавление:
Напомним, что дифференциальным уравнением второго порядка называется уравнение, наивысший порядок производной или дифференциалов в котором равен двум.
Простейшим дифференциальным уравнением второго порядка назовем уравнение вида: 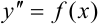 .
.
Например, уравнения 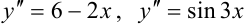 — простейшие дифференциальные уравнения второго порядка. Подчеркнем, что в левой части простейшего дифференциального уравнения находится только
— простейшие дифференциальные уравнения второго порядка. Подчеркнем, что в левой части простейшего дифференциального уравнения находится только 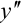 , а в правой — выражение, содержащее только переменную
, а в правой — выражение, содержащее только переменную 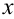 .
.
Для решения простейших дифференциальных уравнений второго порядка необходимо двукратное интегрирование по переменной 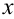 .
.
Рассмотрим принцип решения простейших дифференциальных уравнений второго порядка на следующем примере:
Пример №41.1.
Найдите решение дифференциального уравнения 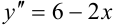 .
.
Решение:
Поскольку перед нами простейшее дифференциальное уравнение второго порядка, найдем сначала 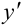 по формуле:
по формуле: 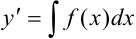 .
.
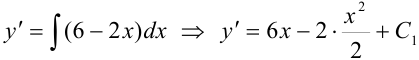 или
или 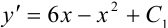 , где
, где 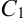 — константа.
— константа.
Для нахождения искомой функции 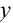 найдем интеграл от
найдем интеграл от 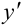 по переменной
по переменной 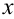 :
:
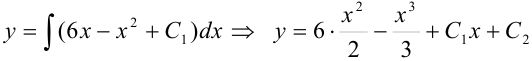 , или
, или 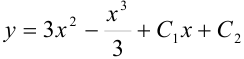 , где
, где 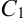 и
и 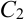 — константы.
— константы.
Полученная функция является общим решением дифференциального уравнения 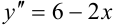 .
.
Ответ: 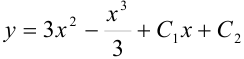 .
.
Отметим, что общее решение дифференциального уравнения второго порядка содержит две произвольные постоянные 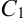 и
и 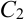 .
.
Для простейшего дифференциального уравнения второго порядка можно рассмотреть задачу Коши (см. лекцию 38). Только в отличие от дифференциальных уравнений первого порядка, необходимо иметь два начальных условия: 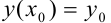 и
и 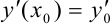 . Для нахождения частного решения задачи Коши можно использовать следующий алгоритм:
. Для нахождения частного решения задачи Коши можно использовать следующий алгоритм:
- Найти
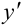 по формуле:
по формуле: 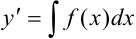 .
. - Воспользовавшись первым начальным условием (
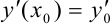 ), найти значение константы
), найти значение константы 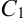 и подставить его в функцию
и подставить его в функцию 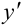 .
. - Найти функцию
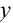 как интеграл от
как интеграл от 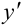 по переменной
по переменной 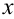 .
. - Воспользовавшись вторым начальным условием (
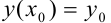 ), найти значение константы
), найти значение константы 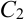 и подставить его в функцию
и подставить его в функцию 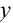 . Полученная функция
. Полученная функция 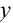 и будет решением исходного дифференциального уравнения.
и будет решением исходного дифференциального уравнения.
Пример №41.2.
Найдите решение задачи Коши: 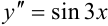 , если при
, если при 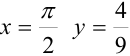 и
и 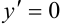 .
.
Решение:
1. Найдем 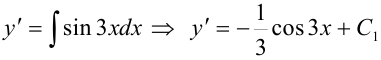 .
.
2. Воспользуемся первым начальным условием: 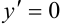 при
при 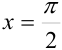 . Подставим эти числа в функцию
. Подставим эти числа в функцию 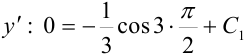 . Поскольку
. Поскольку 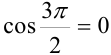 , получим, что
, получим, что 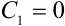 .
.
Подставим найденное значение 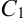 в функцию
в функцию 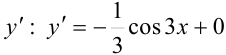 или
или 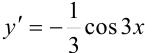 .
.
3. Найдем функцию 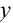 :
: 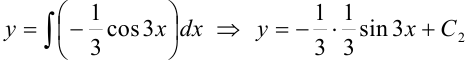 , или
, или 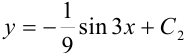 .
.
4. Воспользуемся вторым начальным условием: 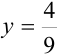 при
при 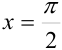 . Подставим эти числа в функцию
. Подставим эти числа в функцию 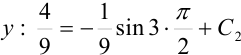 . Поскольку
. Поскольку 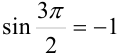 , получим:
, получим: 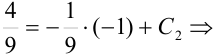
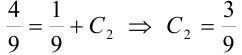 , или
, или 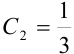 .
.
Найденное значение константы 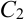 подставим в функцию
подставим в функцию 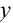 :
: 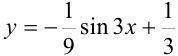 . Полученная функция является частным решением исходного дифференциального уравнения
. Полученная функция является частным решением исходного дифференциального уравнения 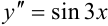 при заданных начальных условиях.
при заданных начальных условиях.
Ответ: 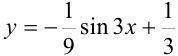 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:

