Оглавление:



Простейшая управляемая нелинейная индуктивность
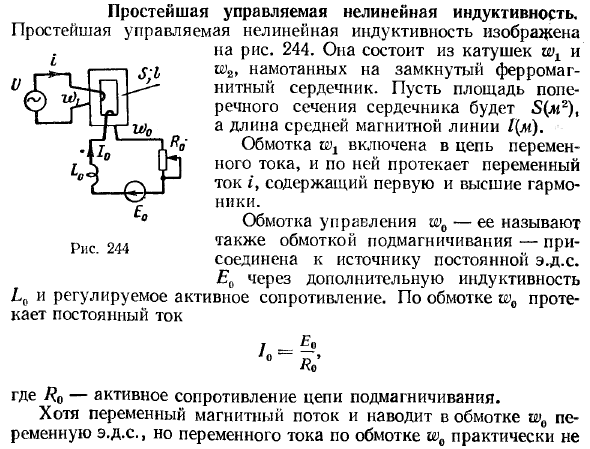
Простейшая управляемая нелинейная индуктивность. На рисунке 244 показана простейшая управляемая нелинейная индуктивность. 244. Состоит из катушки и обмотки 2 вокруг закрытого ферромагнитного сердечника.
- Площадь поперечного сечения сердечника составляет 5 (d (2), а длина линии магнитного поля в центре составляет 1 {м). Обмотка Wj включена в цепь переменного тока, и переменный ток
включает в себя первую гармонику и высшие гармонические потоки. Людмила Фирмаль
Управляющая обмотка ω »0 — также называется намагниченной обмоткой, подключенной к источнику постоянной электродвижущей силы EO с дополнительной индуктивностью Lp и регулируемым сопротивлением. Постоянный ток течет через обмотку w0. Где / 0 — активное сопротивление цепи смещения.
Поток переменного тока индуцирует переменную электродвижущую силу в обмотке, но переменный ток фактически не протекает через обмотку, потому что дополнительная индуктивность Lo берется для формирования достаточно большой индуктивности для переменного тока ,
- Напряжение, приложенное к обмотке, составляет Um cosω /. Это напряжение равно ЭДС. Самоиндукция, приобретенная с противоположным знаком (при условии, что активное сопротивление обмотки wl очень мало): Um cos cot Следовательно, магнитный поток Ф = ~ sinG-J-Фв = Фиsin4-Фо; (9.24) ф = -п »WU’j
Здесь амплитуда переменной составляющей магнитного потока, Фо — постоянная составляющая магнитного потока. Управляя нелинейной индуктивностью,
можно регулировать значение переменного тока i, изменяя значение DC / 0 обмотки y0. Людмила Фирмаль
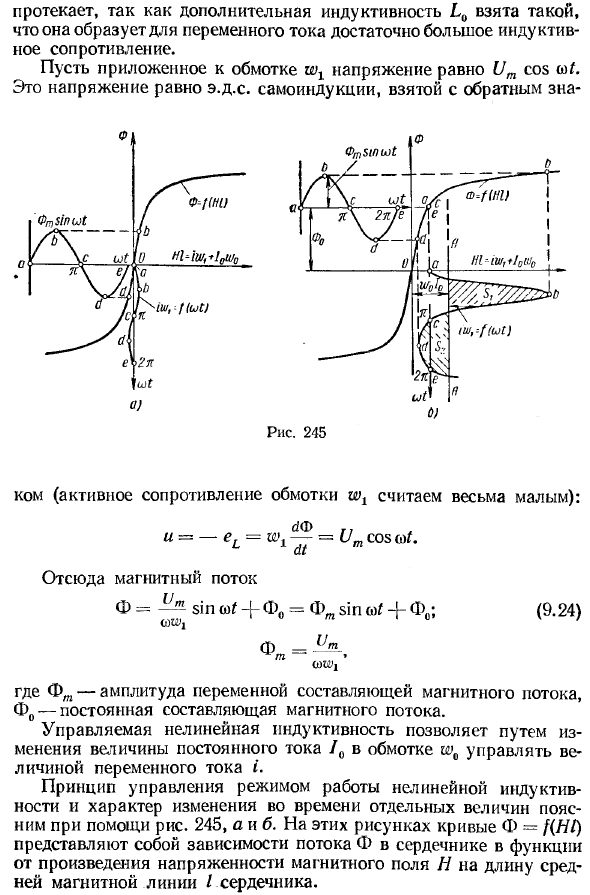
Принцип управления режимом работы нелинейной индуктивности и характером изменения времени каждой величины поясняется с помощью рисунков. 245, а и б. На этих фигурах кривая Ф = представляет собой зависимость потока сердечника Ф как функции от произведения напряженности магнитного поля А и длины линии I магнитного поля в центре сердечника.
Структура 245a на фигуре соответствует случаю / 0 = 0, а в случае фиг.245 b- / 0 = # 0. На обоих рисунках переменная потока компонента O (nsina) Z одинакова. Для фотографий. 245, ® Постоянная составляющая потока равна нулю. 245, bΦ0 = 0,0.
На кривой Φ = f (ω /), кривой Φ = f (Hl) и кривой iwt-f (w /) наиболее характерные точки, соответствующие друг другу, обозначены одной и той же буквой.
Создайте в следующем порядке: 1. Сначала отложите значение постоянной составляющей потока Фо и создайте кривую Фтsin wZ = f (cot) (Рис. 245 и Ф = 0). 2. Затем установите разное время, например, равное © Z-0. l; ~ l; 2l, и для каждого значения, используя кривую φ = / (///), найдите соответствующее значение HI и кривую «f (<° 0 (рис. 245 и Jowo-0)»
Ось времени этой кривой направлена вертикально вниз, и обратите внимание, что ток Z не содержит постоянной составляющей, поскольку обмоточный контур не имеет источника или выпрямителя постоянной электродвижущей силы.
245, b — это нулевая линия кривой iwt = / (coZ), ток i колеблется вокруг этой линии, поэтому среднее значение от /) асимметрична относительно прямой AA Приложенное напряжение Um
Зависимости, которые позволяют рассчитать амплитуду переменной составляющей магнитной индукции W через амплитуду t, угловую частоту co, площадь поперечного сечения сердечника S, а также число витков и постоянную составляющую напряженности магнитного поля, можно рассчитать через DC / 0.
Руководство по формуле. H1t до амплитуды первой гармоники 11t AC и т. Д. (9.25) Фо = (9.26) где B0 — постоянная составляющая магнитной индукции. Из уравнений (9.24) и (9.25), если магнитная индукция измеряется в гауссах, S является этапом 2 и заменяет Um на 1 // 2.
Где U — эффективное значение напряжения на обмотке. (, 271 t 2nfwLS 4.44 ^ 8 уравнение (9.27) позволяет найти амплитуду переменной составляющей магнитной индукции из-за синусоидального напряжения (V, частоты / числа витков wL и амплитуды сечения S. Закон полного тока).
Средняя линия поля произведения Z длины // напряженность поля должна быть равна алгебраической сумме частей на миллион, поэтому | -IowQ = Hl (9.28) Уравнение (9.28) разделено на несколько уравнений Уравнение постоянной составляющей, 1-я гармоника, уравнение 2-й гармоники и т. Д.
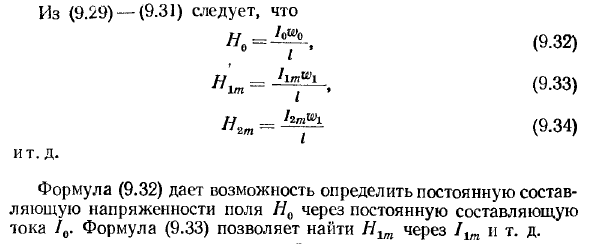
Компоненты уравнения равенства (9.28) левой и правой составляющих h-константы определяются как: = JV / (9.29) где Ho — постоянная составляющая напряженности электрического поля, AC i включает в себя первичные, вторичные и другие гармоники, но цепь обмотки не имеет постоянного источника e, Постоянная составляющая без учета ds и выпрямителя
Амплитуда первой гармоники в левой части уравнения (9.28) является первой гармоникой в правой части уравнения LL = (9.30) где 11t — амплитуда первой гармоники тока t и амплитуда первой гармоники напряженности электрического поля, поскольку (9.29) — (9.31) -Л »®7γ0оА / / / / ^ 1 1 7’1м £ • 77 ^ 2м ^ 1 7 7 2м до j-IT d (9.32) (9.33) (9.34)
Согласно формуле (9.32) постоянная составляющая тока Постоянная составляющая напряженности электрического поля HQ может быть определена через / 0. Используя уравнение (9.33), H1m можно искать / 1m и т. Д.
Смотрите также:
Если вам потребуется помощь по электротехнике (ТОЭ) вы всегда можете написать мне в whatsapp.

