Оглавление:
Простейшая оптимизационная задача
Напомним общие методы решения простейших оптимизационных задач с ограничениями-равенствами. В этих методах обычно с помощью ограничений переменные выражают друг через друга и подставляют в целевую функцию, после чего требуется найти безусловный экстремум целевой функции, который и является решением задачи.
Задача:
База берет на себя обязательство хранить товар и выдавать его потребителю в объеме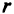 
тонн ежедневно. Стоимость хранения товара 
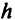рублей за I тонну в сутки. База может получать товар только равными партиями 
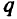тонн и через равные промежутки времени 
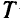. Стоимость хранения запаса товара 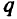в течение времени 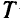равна 
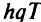. Загрузка базы товаром и подготовка к его приему обходится базе независимо от количества товара в 
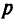рублей. Очередной завоз товара производится в момент выдачи предыдущего. Требуется определить оптимальный объем порции товара 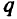и интервал его поставки 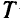, при которых суточные затраты базы были минимальными.
Решение. Суммарные суточные затраты базы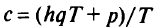 
— функция двух переменных 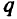и 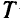. Дополнительное условие 
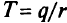. Минимизируемая функция
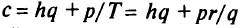
функция одной переменной 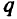. Чтобы найти значение 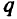, при котором с будет иметь минимальное значение, определим производную 
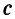по 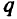и приравняем ее нулю:
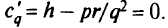
Отсюда
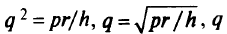
не может быть по смыслу задачи отрицательно. Чтобы установить вид экстремума функци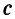и при
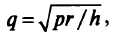
найдем вторую производную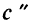 
по 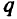и определим ее знак при
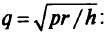
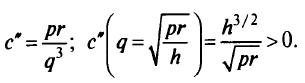
Отсюда следует, что функция 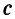при 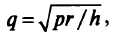достигает наименьшего значения. Оптимальный интервал поставки товара
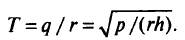
Суточные затраты при этом
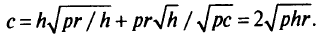
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:
