Оглавление:
Пропорциональные отрезки. «Золотое сечение»
В геометрии часто встречается понятие пропорциональных отрезков. Дадим соответствующее определение. Ненулевые отрезки а и b называют пропорциональными отрезкам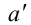 
и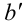 
, если их длины удовлетворяют пропорции 
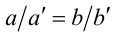, т.е. а относится к 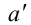так же, как b относится к 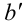. В этом случае действительное число k , равное отношению 
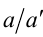, называют коэффициентом пропорцио-нальности, и тогда условие пропорциональности двух отрезков можно записать в виде
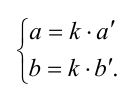
Порой возникает необходимость записать условие пропорциональности трёх пар отрезков. Приведём определение для этого случая. Ненулевые отрезки а ,b ,c называют пропорцио-нальными ненулевым отрезкам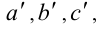 
если справедлива двойная пропорция
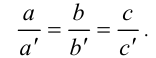
И в этом случае действительное число k , равное каждому из этих отношений, называют коэффициентом пропорциональности, и условие пропорциональности трёх пар отрезков можно записать тогда в виде системы
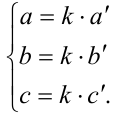
Пусть дан отрезок длины c. Разделим (рассечём) его на два отрезка длины а и b , т.е. c = а + b . Пусть при этом выполнено условие
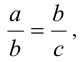
т.е. меньший отрезок относится к большему так, как больший — к их сумме. Эту пропорцию можно записать в виде
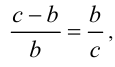откуда следует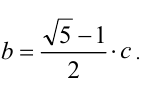 
В Древней Греции такое деление отрезка на две части получило название деления в среднем и крайнем отношении. Гораздо позже великий Леонардо да Винчи назвал такое деление «золотым сечением», а Лука Пачоли — «божественной пропорцией». Такие названия связаны со многими замечательными свойствами сечения. Не последнюю роль в этом играли эстетические соображения: например, прямоугольник, отношение длин сторон которого равно числу
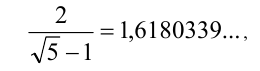
хорош для восприятия, выглядит гармонично для человеческого глаза. Он называется прямоугольником золотого сечения. Видимо, по этой причине «золотое сечение» использовалось издавна в архитектуре. Интересно, что если от такого прямоугольника отрезать квадрат максимальной площади, то останется вновь прямоугольник золотого сечения. Примером «золотого сечения» может служить стандартный, формата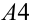 
, лист писчей бумаги: сложенный пополам, вчетверо и т.д., он сохраняет первоначальную пропорцию.
Золотое сечение часто встречается в различных задачах. Рассмотрим одну из них, устанавливающую связь золотого сечения с пятиконечной звездой.
Пример №117.
Вписать в окружность правильную пятиугольную звезду.
Решение:
Простой способ построения правильного пятиугольника предложил Клавдий Птолемей (ок.100-ок.178). Он писал: «Имеем полукруг ABC, описанный около центра О на диаметре АОС .
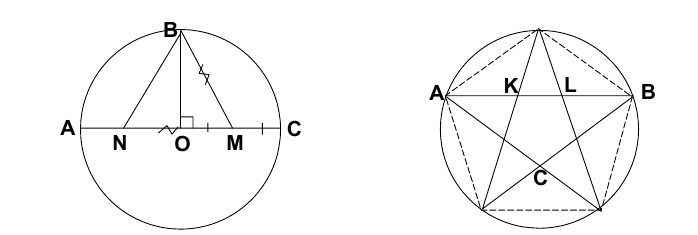
Проведём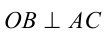 
в точке О. Разделим отрезок ОС пополам в точке М , проведём прямую MB и отложим отрезок MN = MB . Соединим N с В отрезком NB . Тогда NB — искомая сторона правильного пятиугольника, вписанного в данную окружность». Доказательство этого утверждения приводится в книге. Более того, каждый из отрезков AB,AL,AK,KL на рисунке справа ровно в 
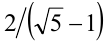раз больше последующего! По-видимому, в связи с этим замечательным свойством пифагорейцы выбрали пятиконечную звезду в качестве своего талисмана: она считалась символом здоровья.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
| Числовые равенства и неравенства |
| Числовые равенства и их свойства |
| Числовые неравенства и их свойства с примерами решения |
| Основные формулы сокращённого умножения в математике |
