Произвольная пространственная система сил

Оглавление:

Это изображение имеет пустой атрибут alt; его имя файла - image-10-1.png

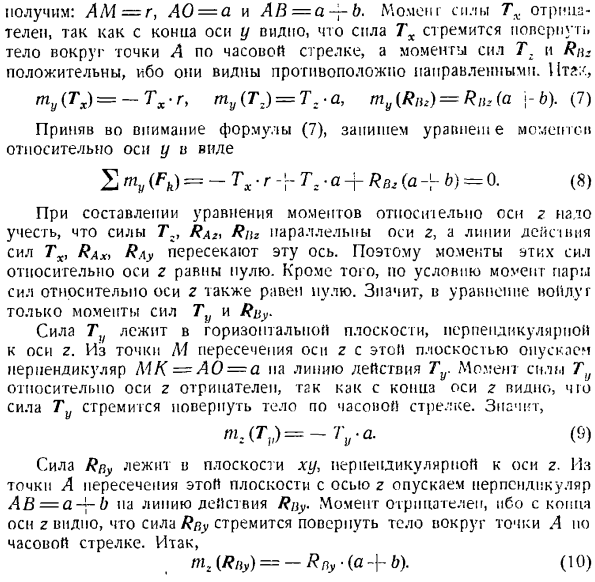
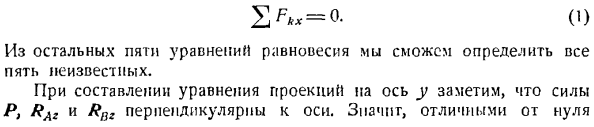
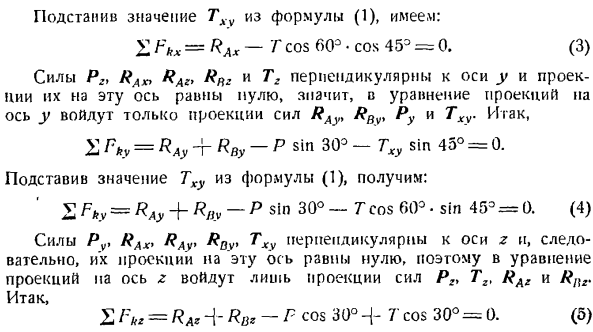
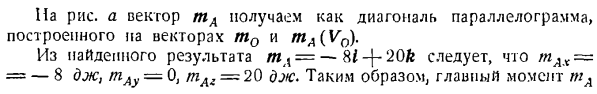
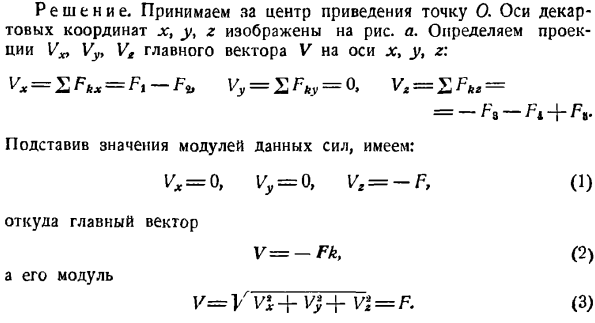
Произвольная пространственная система сил

Любая пространственная система сил Момент силы против 1 пункта. Момент силы вокруг оси. Теория спящего в пространстве. Для плоской системы сил момент силы относительно точки определялся как алгебраическая величина: m @(F)= z \ z Flu 2 R «1 S. f） Рисунок 2.4. .

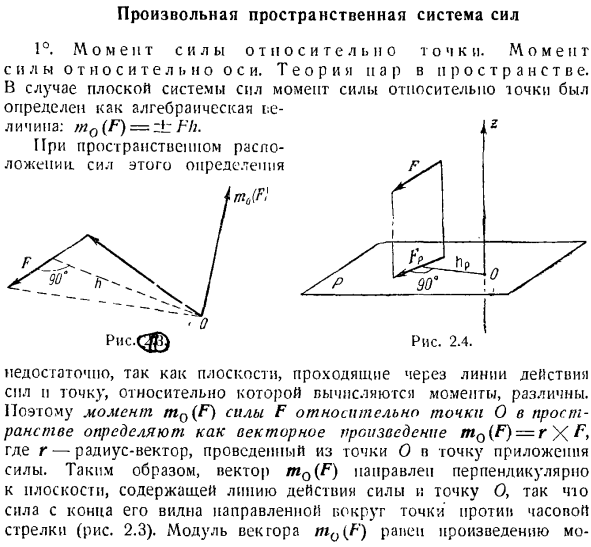
Таким образом, момент силы F относительно точки O в пространстве m0(F)определяется как векторное произведение m0(F)= r \ F. где r-радиус-вектор от точки O до точки действия силы. Таким образом, вектор mQ (F) направлен перпендикулярно плоскости, содержащей линии действия силы и точку O, так что»по силе от края мы можем видеть вокруг точки против часовой стрелки (рис.2.3)».

Этого недостаточно, потому что плоскость через линию действия силы и относительная точка, в которой вычисляется момент, различны Людмила Фирмаль

Модуль вектора m0 (F) равен следующему произведению: OA-a. момент силы отрицателен, потому что сила Fxz стремится вращать тело в плоскости xy по часовой стрелке вокруг точки O. So … tu (T)= — Fxta = — Fa cos 30°= — Fa%3. К задаче 2.4. т. осталось определить силовой момент F относительно z-axis. To для этого найдите проекцию значения Fxy силы F на плоскость xy, перпендикулярную оси Z. Теперь рассчитаем момент Fxv силы относительно точки O пересечения оси z и вертикальной плоскости с xy.

Плечо-это отрезок OA = A. знак момента положителен. Это происходит потому, что с конца оси z получается, что сила Fxy стремится повернуть объект в плоскости xy против часовой стрелки вокруг точки O. означает Фа *(F)= FHua—2 Задача 2.5.Определите момент для осей x, y и z силы F, показанной на рисунке.

Сила, приложенная к точке A на оси y, составляет около −30°F, и вся проекция этой плоскости равна угол с плоскостью xy; формировать y-оѕь и угол OSA 45°. Оа = а. Решение. Как и в предыдущей задаче, можно легко найти момент силы F относительно оси Y и Z \ МВ (ф)= 0 (линия действия силы F пересекает ось Y), м2 (/7)= — / Вы. Здесь Fxy = F cos 30°= — модуль для проецирования силы F на плоскость xy, perpediq- 1/2. » линейный по оси z, a / 2 = 0,4 sin 45°= a sin 45°= a ^-

(Знак момента отрицательный. Это происходит потому, что с конца оси z мы видим, что сила Fxy стремится повернуть тело в плоскости xy по часовой стрелке вокруг точки O.） м(ф)=0.тлп=—П-. (Да Труднее найти момент силы F относительно оси x, так как угол между силой F и плоскостью yz, перпендикулярной оси x, неизвестен.

Длина перпендикуляра, опущенного из точки пересечения плоскости xy и оси z на линии действия силы Fxv. Людмила Фирмаль

Здесь рекомендуется прибегнуть к методу, описанному в обзоре теории-разбиение силы F на 2 составляющие. Разборка Применить силу к компоненту найти л ФЗ(см. Рисунок).Так, Ф = найти + ФЗ>где найти = соѕ Ф «30°, ФЗ = Ф соѕ 60°. Теперь мы применяем теорему Вариньона для определения момента F силы на оси X.

Таким образом, момент равнодействующей силы на оси равен сумме моментов составляющих сил на той же оси. smallp. In это дело МХ (Ф)= МХ(Fxy) — л МХ(ФЗ). (2） Линия действия силы Fxy пересекает ось xy, поэтому mx (Fx>)= 0.Момент силы относительно оси л ФЗ. tx (Fz) = равно Fta. Для FZ = F cos 60°= Fj% конечный результат равен: mxif)=(3） Л. * для вычисления силового момента F относительно оси x можно также воспользоваться следующей формулой: человек = автор zFyt(4）

Где Y и Z-координаты точки приложения силы F и fy и FZ-проекции силы F на оси Fy = — Fxy cos 45°= — F cos 30J cos 453 =- К задаче 2.5. Y и Z. В этом случае, г-а, з = 0、 FZ = F cos GO3 ==〜. Подставляя эти значения в Формулу(4), Вы получаете результат по формуле (3). То есть mx (F)= y. Как показывает решение задачи, если расчет момента силы на оси обычным методом затруднен, то следует опираться на разложение компонента силы-па, последующее применение теоремы Вариньона или формулы момента силы на оси по проекции силы-па (3).

Задача 2.6. вычислите главный момент на оси x, y, z и точку О пространственной системы сил, показанной на рисунке. Мощность Fx находится в конце Куба, а мощность Fq и F ’ 3 находятся на диагонали этой стороны. Ребро Куба a равно 2 м,/ ^ = 10 i,= = F3 = 12 | / / 2 и… Решение. Главный момент системы сил относительно оси равен сумме моментов этих сил относительно этих осей.

МХ =тmx(ФК),wц = г] ту {ВН) Т МЗ =£г (Фу б = я В этой задаче А = 1 к = 1 МХ = МХ(Ф)+ МХ(ф) — ф МХ-му =(Z7 резца.)/гг,(Ф) — ведется аналитическая (в FJ,= Ш, (Ф.)+ н(ф) + МЗ(Ф3). Относительно силового момента F] t и оси*, и И г доступны следующие формы:’), (Fr)=далее、 (КТ)= Ф, грех = ту(Фи)= — FJi = — Ф, грех 45°= — Т.(Ф. 2) = соѕ Фи 4О°а = 2, (^3) = Мой(Ф2) = МЗ(ФА)= 0 (Линия действия силы F3 проходит через точку O. то есть она пересекает оси x, y, r). Вводя значение моментов этих сил в Формулу(1), получаем: (Да т.

г. Л. 0 лет\ s Так… г, Б. К задаче 2.6. Координата карты r является проекцией главного момента m0 на начало координат O на соответствующую ось одновременно, то есть m0 = rnJ mYj + m __ G2l У2 милливольт= тг = Р \ АП— » 2— Или замените измерения. / 7 * ^ = 24 Дж, ту = −24 Дж, МЗ = 44 ДМ

Основные моменты системы сил на осях tx, / yau, t2 т. Два Икс Числовое значение Хумк О города и его директор коссейн： Т0 = м%т «р = 55.5 Дж、 соѕ(х? М0)= 0.43, потому что(> почтовый индекс cm0)= г = −0.43 тогда потому что(iTm0)= ^ = 0.79、 О То есть (n%w0)= 05°, (y, m0)= M5°, (2,m0)= 38°.Таким образом, m0 =(24i-24 / — J-44ft). 2°.1. сведение к одному центру силы в любом месте пространства.

Основной вектор V н. Силовая система называется векторной суммой этих сил, то есть V-Fk. Пока. Проекция главного вектора V на оси декартовых координат Vx, Vv и Vz равна сумме проекций сил на соответствующие оси. В’.в = fkx, уу = г] fky по, ’ П2 = гиг£. (9 *） Модуль основного вектора V P направляющего Косинуса определяется по формуле. В / = г в. в} + Ви(с *） потому что(Вац)= — J, а потому что(ый)=£, потому что(>)=%. (И）

Главный момент m0 пространственной системы сил против центра O повреждается векторной суммой моментов всех сил против этого центра. н. М0.= 2> 0（/ =•）。 Проекция главного момента m0 на декартову координату mz%, можно определить модуль и направление Косинуса m0 по формулам (7) и (8).

Если мы приведем произвольно расположенную в пространстве силу к 1 центру, то система сил будет равна паре сил, равных основному вектору V, а момент Топо 1 века равен паре сил, равных основному моменту m0. Изменение центра системы сил, вообще говоря, изменяется главный момент системы, зависимость главного момента системы сил от выбора центра выражения выражается следующим образом: главный момент системы сил от нового центра a tA связан с главным моментом системы he моментом, связанным с новым центром A силы v, добавленной к старому центру o: ma = M0 ^ -Ma (v0).

Статические инварианты пространственной системы сил — это характеристики этой системы, которые не меняются при изменении центра торможения. Есть 2 статические инварианты. Первым статическим инвариантом является главный вектор V системы forces. By определение, величина и направление главного вектора V не зависят от выбора центра редукции. Г = ЮА + Vyj-Т ГЛ Где Vx, Vyi V2 определяется по формуле (O).

2-й статический инвариант-скалярное произведение главного вектора V и главного момента m0-не зависит от выбора центра вырождения. Vm0 = Vxm х-\ — выть / ий V2m, Т Где Vx, Vyt V2 и/ nx, m и tr определяются уравнениями(9 }и (5) соответственно (6). Результатом является сила эгова, которая соответствует определенной пространственной системе сил, а сила V соответствует определенной системе сил только тогда, когда момент объединяется с парой сил, равных основному моменту, поэтому сила V не равна силе Р результата.

Различные случаи уменьшения произвольно размещенных сил в пространстве А) главный вектор равен нулю, но главный момент не равен нулю, т. е. V = 0, и^ 0 Система сил сводится к паре сил, в которой момент равен главному моменту (в этом случае главный момент системы сил не зависит от выбора центра редукции). б) основной вектор не поврежден пулями, но основной момент равен нулю, то есть V t / B0, то= 0.

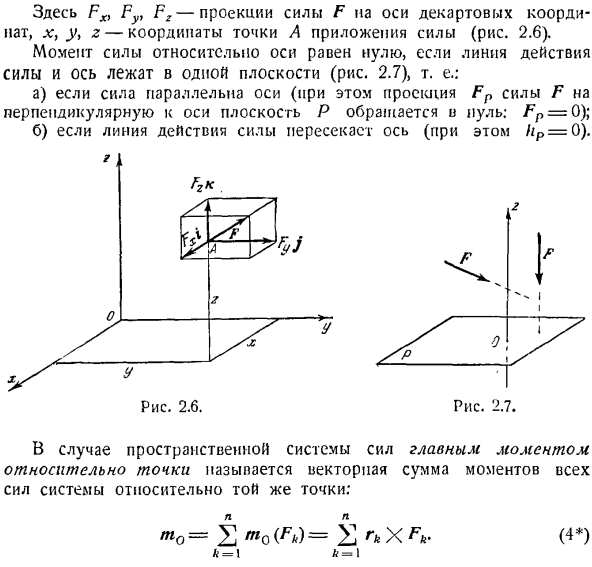
Система сил прикладывается к центру системы торможениярезультат задается В. i) основные векторы и моменты системы не равны нулю, более того, они перпендикулярны друг другу. V ^ 0, m0 y * 0, (moTv)= 90°. Расстояние силы от дула расстояние от хомута до линии действия силы (плеча), т. е. \ nt0 (ф)\ = ф / я Момент силы относительно оси mz (f) (рис. 2.4) определяется как произведение модуля проекции силы Fp на плоскость P, перпендикулярную оси zy, и произведения пересечения этой плоскости и проекции оси из точки O на проекцию силы действия, действующей на ось Z.

Если сила Fp пытается полагать видна с конца оси z) объект вокруг точки O находится против часовой стрелки, если она по часовой стрелке, то момент положителен Стрелка, потом минус, то есть тг(Ф)= ЗТ Ффип. Силовой момент F 2.4, показанный на рисунке, положителен по отношению к оси Z.

Таким образом, момент силы относительно точки является вектором, а момент силы относительно оси-алгебраической величиной. Если точка лежит на оси, то момент силы относительно оси будет равен моменту проекции силы относительно точки на оси Муе. То есть, РНЗ(Ф)= арг М0(Ф) (рис. 2.5).

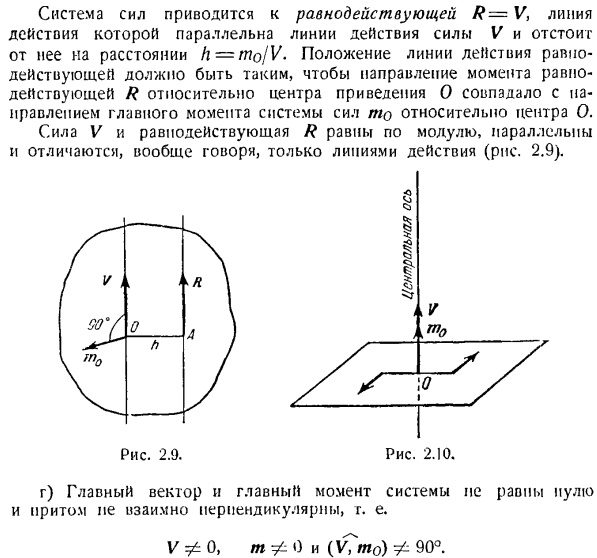
Система сил сводится к результирующей R = V>, линия действия которой параллельна линии действия силы V, разделенной расстоянием h = mojV. Положение линии действия соединения должно совпадать с направлением момента соединения R относительно восстанавливающего Центра O, а затем относительно центра основного момента системы сил.

Сила V и результат R равны по величине и параллельны г) главный вектор и главный момент системы не равны нулю, более того, они не взаимно перпендикулярны. V ^ 0, tp 0 и (\т0) −90°. Система сил сводится к динамо-машине (силовому винту).Сила V представляет собой комбинацию пары сил в плоскости, перпендикулярной этой силе.

Линия действия силы V называется центральной осью. Центральная ось-это геометрическое положение центра торможения, а величина основного момента минимизирована и ориентирована вдоль этой оси(рис. 2.10).Форма уравнения центральной оси имеет вид Техас-yVz + звв _ мой — 2Vx + ХВЗ тнз-xVu + yVx Ух ~~ «в»〜ВЗ Где mx, mv, m2, Vx> Vy, V2 имеют одинаковое значение, а x> y, z-текущие координаты. д) главный вектор и главный момент системы равны нулю, то есть V = 0, m0 = 0 Твердое состояние, к которому приложена пространственная система этой силы, находится в равновесии、

Уравнение равновесия твердого тела под действием любой космической системы сил. Для равновесия твердого йода под действием любой пространственной системы сил необходимо и достаточно, чтобы сумма проекций всех этих сил на произвольно выбранные оси декартовых координат x, y, z и сумма моментов всех сил на этих осях были равны нулю.： 2 rhx =°< си= \ н. Два Л-1. н. Два Л -! Fftj = 0, (12 *） (13 *） 2 м, (БПФ)=0,1 ″» * 1

Первые 3 уравнения называются проекционными уравнениями. Пусть главный вектор V равен нулю. Последние 3 Уравнения называются Моментными equations. So что главная точка равна нулю Для пространственной системы произвольных сил задача определяется статически, если число алгебраических неизвестных равно 6 или меньше.

В случае жесткого равновесия с 1 неподвижной точкой (рис. 2.11), например сферическим шарниром, система активных сил сводится к результату, линия действия которого проходит через неподвижную точку. Движение-свободное/] точка роя на оси декартовых координат, 3 проекции реакции роз определяются из уравнения (12). 2 ^ Два 1. Из уравнения момента(13) можно определить неизвестные значения 3 активных сил(все силы, не связывающие реакции, называются активными).

Для равновесия твердого тела с 2 неподвижными точками, например 2 сферическими шарнирами или 2 упорными подшипниками (рис. 2.12), можно определить значения 4 составляющих опорных точек RLhu / gdu, RftX.? 。Значения компонент поддерживающих реакций Raz и Rn2, направленных вдоль этой оси, не могут определяться индивидуально. Вы можете найти общий раз — > Rbz только-если 1 из подшипников выполнены в виде подшипника B (рис. 2.13), то реакции компонентов Rb2 нет, потому что они могут двигаться вдоль z-axis. In в этом случае из уравнения равновесия можно определить значение 5 компонентов опорной реакции Rax> Yalu> Raz> Rbxi Ray, а также Значение 1 активной силы.

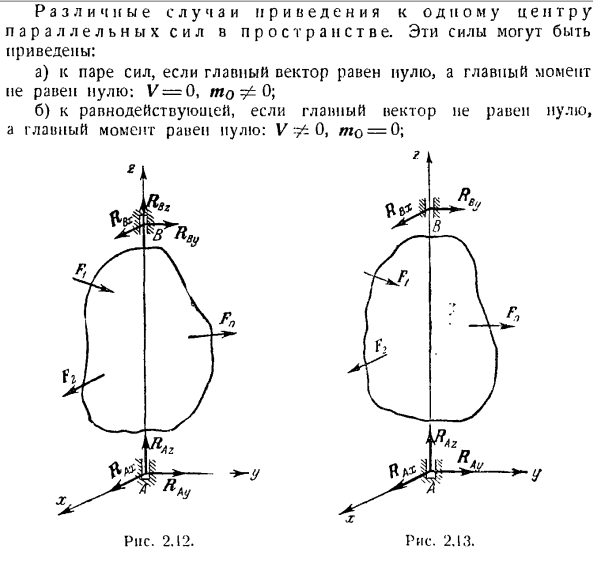
1. разные случаи приведения параллельных сил пустоты к своему центру. Может дать вам эти силы： а)если главный вектор равен нулю и главный момент не равен нулю, то 1 пара сил: V-Q, то^ 0; Б)если в результате основной вектор не равен нулю、 Рисунок 2.1.г. Рисунок 2.12. в) в результате, если главный вектор и главный момент не равны нулю: V ^ 0, ТО^ 0; для системы параллельных сил векторы V и векторы всегда перпендикулярны друг другу

г)если главный вектор и главный момент системы равны нулю, то твердое тело находится в равновесии: V = 0, / mo = 0 уравнения равновесия для системы сил, параллельных оси z:: 2 = 2 ^ х(ФК)= 0т ж] мой(Ф / 4)= 0.(14*) л — я М = 1 м * = » я Если алгебраические неизвестные равны до 3, то задача определяется статически. Решая задачу твердого равновесия при действии на космическую систему любой силы, первые 4 В начале и в начале очереди, и Страница 15. Следующий：

5) убедитесь, что эта задача определена статически, то есть алгебраические неизвестные составляют до 6 штук. 6) Выберите ось системы декартовых координат. 7) создает твердое тело (12) и (13) 6 уравнений равновесия. В случае системы параллельных сил, 2 уравнения проекции сил на ось, перпендикулярную силе и 1 момента силы на ось, параллельную силе disappear. So, если сила параллельна оси x, то уравнение равновесия принимает вид: 2 факс= 0> 2 «’»（**）= 0、2>» DGl)= 0; k-1 * = I 1 8) после решения системы уравнений, суммированных в предыдущем пункте, найдите неизвестную величину. Рекомендуется использовать декартовы оси

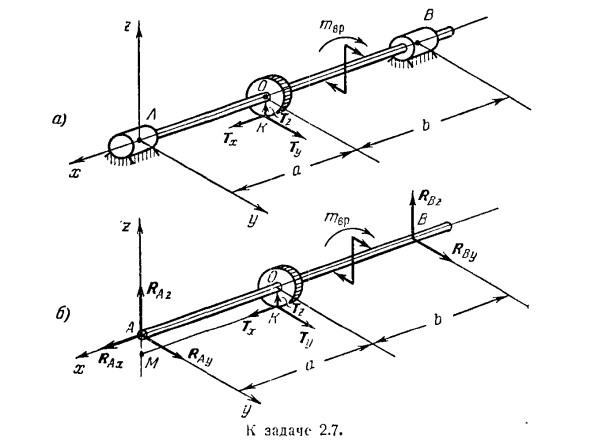
Задача 2.7.На рисунке радиус l, прикрепленный к горизонтальной оси, показывает винтовые передачи. Вал состоит из 2 подшипников: упорный подшипник A и цилиндрический подшипник B. At точка K на вертикальной плоскости симметрии шестерни, давление T прикладывается к зубу со стороны другой шестерни, которая зацепляется с ним (на рисунке A, T и 2-я силовая передача не показаны).

Давление T разложено на 3 составляющие Tx> T} / и T, которые параллельны осям x, y и z соответственно (начало координат находится в точке A, ось x ориентирована вдоль вала, ось z вертикально вверх, а ось y образована осями x и z).Некоторая сила крутящего момента gpr приложена к равномерно вращающемуся валу так, что момент относительно оси равен: mx =niBp, my = m2 = 0 Поддержка a n B и определяет реакцию SPR вращающего момента. Показаны модули компонентов Tx, Tu и Tg давления T, приложенного к зубьям зубчатых колес. Размеры показаны на рисунке.

Игнорируйте вес шестерни и вала. Решение: как определить неизвестную реакцию и крутящий момент опор а и в? Рассмотрим равновесие вала, на котором крепится шестерня. (Равновесие вала означает не только покой, но и его равномерное вращение, о чем говорится в положении дел.） Как показано на рисунке, к валу и шестерне прилагается следующая активная сила.3 составляющие давления TX, Tu} T2 и момента mx = mR?

Необходимо определить (в этом вопросе момент действия пары активных сил неизвестен). Муфта, наложенная на вал, представляет собой 2 подшипника упорного подшипника A и подшипника B. мысленно отбросьте муфту и исправьте действие против вала реакцией. Смогите быть двинуто с подшипником B Таким образом, остается нарисовать только 2 компонента Rny и Rn2i, которые не имеют компонентов реакции вдоль оси x и перпендикулярны оси оси. (Эти компоненты на рисунке B указывают в направлении увеличения соответствующих координат.

Если на самом деле направление компонента противоположное, то ответ будет отрицательным.) Упорные подшипники A, В отличие от подшипников B, не могут перемещать вал вдоль x-axis. So, в пункте а, все 3 компонента Rax, Ra?> Показывает реакцию Ra2. Силовой момент для оси декартовых координат mk(F), tu (F)} mz (F)>начало координат O и величина силового момента m0 (F) для его Косинуса направления Я> если ч0)я = ДМС(ф)+ л(ф)^ Мун (П cos = cos [y7rn0 (Z7)] => Где tn0(Ф)= Х(ф)Я-J-мой (Ф) и J-(- МЗ(Ф) К. Формула момента силы на оси декартовой координаты с проекцией силы на эти оси задается формулой: (==YFz-zFy в y (F)= z\: x-xF Z) mz (F)= xFy-yl ^(3 «）

Таким образом, мать должна учитывать равновесие свободного вала с шестерней под действием активной силы Tx, T] T Tg и пары сил момента mx =m0p, а также компоненты реакции r,\ x, Rav> Riz> Riiy >iz-6. система. Поскольку число алгебраических неизвестных также равно 6 (mup, R,\ xt Dow, Raz * RJiy и Rvg), задача определяется статически. Создайте уравнение для проекции СГС на ось декартовой координаты xy, Z.

Все силы перпендикулярны или параллельны этим осям. Таким образом, их проекция будет равна нулю, или величине соответствующей силы. Таким образом, силы пары forcestu, Tg, RAyy R \ Zi Rny, Ritz h перпендикулярны оси x, и поэтому проекция на эту ось равна нулю. из проекций на ось x только R4l и Tx ненулевые, и обе проекции являются positive. So … HfMx = ТХ-\ — РА * = О (1） Аналогично опишем уравнение проекции сил на оси y и Z. И = Ра; + Рбз =о. (ч） (Напомним, что вектор лавы пары сил равен пуле, поэтому проекция пары сил на ось лампы равна нулю.）

Приступим к составлению уравнения момента силы относительно осей x, I/, Z. прежде всего, следует отметить, что построение этих уравнений в данном вопросе достаточно simple. In дело в том, что нет необходимости проектировать плоскость, перпендикулярную этим силам и осям, так как линия действия силы параллельна или пересекает координатные оси, поэтому она имеет момент, равный пуле, или сила находится в плоскости, перпендикулярной оси. при составлении уравнения момента силы относительно оси x сначала отметим, что силы R \ x и Tx параллельны оси x, а линии действия сил R,\ v, R \ iy Tz> Rny и Rrs пересекают ось X.

Следовательно, эти моменты будут равны нулю. Это означает, что только момент T силы и пара сил входят в уравнение момента. По гипотезе момент пары относительно оси x равен/ ivr. МХ = ФСФ. (4） Сила Tu находится в плоскости, перпендикулярной оси X. Из точки O на пересечении оси и плоскости опустите перпендикуляр OK = g к линии действия Ту.

Сила видна с края оси x, что сила Tu стремится повернуть тело против часовой стрелки вокруг точки O, поэтому момент равен positive. So … МХ(Тай)= Тая-Р (5） Используйте уравнения (4) и (5) для описания уравнения момента для оси X. 2lmx(FН)=карту±телевидение. р = В.(6） При создании уравнения

Вы получаете LM = r, AO-a и AB = a-rb. My мощность r является отрицательным Tx. Поскольку Tx стремится вращать тело по часовой стрелке вокруг точки A, сила T. И поскольку момент R \ 2 положителен, его можно увидеть с конца оси Y. Золото./ *、 ПУ(Техас)=—Техас’g, мой (Т2)= т:-а моя(р, ч)= Rlh(ди джей-б). (7） Принимая во внимание формулу(7), запишите момент равновесия для оси y в виде: 2nLpk)= — Tx’R-rTr ’ < * + * vLa + b)=0.(8）

при составлении уравнения моментов относительно оси z необходимо учитывать силу. Riu параллельна оси z, а линии действия TX1 пересекают эту ось с RAx, R и\ y. таким образом, момент этих сил относительно оси z будет равен bullet. In кроме того, в зависимости от условий момент пары сил относительно оси z также равен нулю. Таким образом, в уравнение входят только моменты силы силы Tu и Rl {Y. Сила Tu находится в горизонтальной плоскости, перпендикулярной оси Z. от пересечения M оси z и этой плоскости опустите перпендикуляр MK = AO = a к линии действия Ту.

Силовой момент Tu относительно оси z отрицателен. Это связано с тем, что от края оси z сила Tu стремится повернуть тело по часовой стрелке. Средства МЗ(т])=—ты проверено. (9） Сила R (iy) находится в плоскости xy, перпендикулярной оси Z. От пересечения A этой плоскости и оси z мы опускаем перпендикуляр AB = a — > — B. рабочая линия Ruy. Момент отрицательный.

Существует тенденция вращать тело по часовой стрелке вокруг точки А. МЗ(моего)= — моего(А + Б). (10） Опишем уравнение силового момента относительно оси z с учетом уравнений(9) и (10). 。 ЕМТ (ФК)= — ТВ-а-лучей.(A + b)= 0 (11） Итак, уравнение равновесия вала с неподвижной шестерней принимает вид: 2 Fby = ту-Ф-Луч-Джей — моего = 0,2 Фкт = ТЗ + Рал-Джей РБ; = 0,2 МХ(ФК) = МВР-Ф ту-Р = 0, илмий(FН)= — ТХ. р — \ — т — а-j-Кя,.(Н -|)) = 0、

Где 6 неизвестных(Rax> Ra?> Raz> RBy * Rbz » / pvr) к решению этой системы, состоящей из 6 уравнений. Из уравнения ((i), Tu-r. правда, от края оси x видно вращение пары по часовой стрелке. Техас-г-тг-в Р. си Из уравнения (11)можно увидеть: Р —Туа 1 < хорошо— си’ Здесь, подставляя значения RBy в Формулу (2) и R8z в Формулу (3), получаем соответственно следующее: Я-б-я-ТХ-р + т. з.-Ай Б А + Б * aJrf. Наконец, из (1)следует RAX = — Tx.

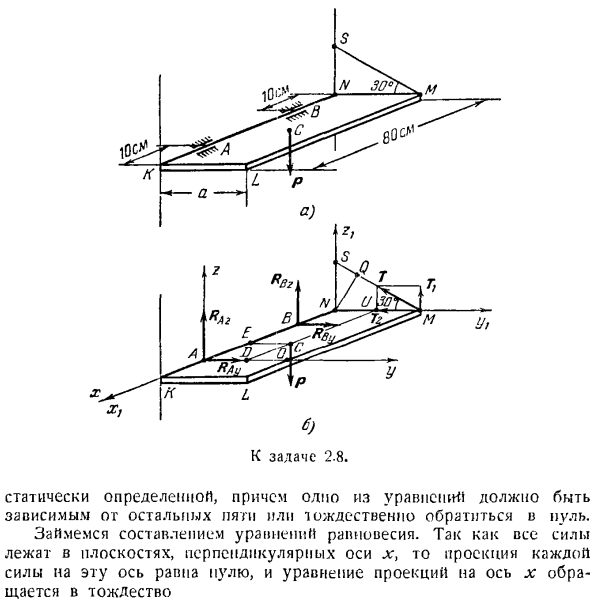
Значения для {RAx}, RAy, RAz и RBy были отрицательными. Это означает, что направление силы R Ax, RAv, RAZ, R [iy противоположно тому, что показано нами на рисунке*. Знак Rllz становится понятным только после замены чисел Tx, a, r. Задача 2.8.Багажники рельсового транспортного средства крепятся к стенке транспортного средства с помощью шарниров (цилиндрических шарниров) а и В, а также штока АФС.

Стержни, соединенные с полкой и стенкой шарнирами M и S, образуют горизонтальную поверхность полки и угол 30°. Если масса полки I = 10а, определяют реакцию L и стержня A1S с петлей L; D. размеры показаны на рисунке. The solution. To определите искомую реакцию петель A и B и стержней, рассмотрите равновесие шельфа KLMN.

На полках 1 действует активная сила-ее собака Р = 10 кг, с прикладывается к центру тяжести полки (точка пересечения диагоналей прямоугольного КЛМН (рисунок б)). Применяя закон высвобождения, мысленно отбрасываем связи, то есть петли а и В, и стержни АФ Си Си, корректируя воздействие на полки с помощью соответствующей реакции связывания.

Реакция t стержня направлена от Ж до S вдоль rod. It не представляется возможным сразу указать направление реакции петель а и В. Однако, поскольку шарнир (цилиндрический шарнир) не препятствует перемещению полки вдоль оси АВ, вдоль этой оси отсутствует компонент реакции. Это означает, что реакция направлена перпендикулярно оси AB, и каждая из них может быть разложена на 2 взаимно перпендикулярные части.

После выбора начала координат декартовой системы координат в цикле A нарисуйте ось x вдоль A B, ось y горизонтально вправо, а ось z вертикально вверх. В зависимости от выбора координатных осей показаны компоненты реакции RAv, петля A Raz и петля B RBz(см. Рисунок B). Таким образом, полк КЛМН находится в равновесии под действием активных сил-массы Р и 5 неизвестных сил: Рав, разы рный РНЗ, т. к. все эти силы образуют пространственную систему сил, поэтому число уравнений равновесия равно 6.So задача такая Кроме того, 1 из статически определенных уравнений будет зависеть от других 5 уравнений или маркироваться точно таким же образом. Давайте создадим уравнение равновесия.

Поскольку все силы находятся в плоскости, перпендикулярной оси x, проекция каждой силы на эту ось равна пуле, а уравнение проекции на ось x является тождественным. S Fkx = 0. Из других 5 уравнений равновесия мы можем определить все 5 неизвестных. при составлении уравнений проекции на ось y обратите внимание, что силы Pr RA: и Rn перпендикулярны оси. Значение, отличное от нуля (Да

Где: Fx, Fyi, Fz-проекция силы F на ось декартовых координат, а x, y, r-координаты приложенной точки A силы (рис. 2.6). Если линия действия силы и ось находятся в одной плоскости, то момент силы относительно оси равен нулю(рис. 2.7). а)если сила параллельна оси (проективная Fp силы F на плоскости P перпендикулярна оси будет пуля: Fp = 0）; Б) если линия действия силы пересекает ось(в этом случае cr = 0);

Рисунок 2.6.Рисунок 2.7. Для пространственной системы сил главный момент является относительно тонким и векторная сумма моментов всех сил системы к одной и той же точке. «о = 2, С7 *)= 2(4 *） к = \ к = 1 Проекция силового луча, Rliv и только T. Поскольку силы Ray и RBy параллельны оси Y, проекция на эту ось равна Ray и RByl, и проекция на силы Т равна-Tcos 30е, проекция уравнения на ось Y имеет вид: = Клу + КПУ-Т соѕ 30 ^ =0.(2） при составлении уравнений проекции на ось z учтите, что силы RAy и RBy перпендикулярны оси z, а их проекции равны нулю.

Силы RAz, RBz и P параллельны оси z, а проекции на эту ось равны RAz> RBz и-P. наконец, проекция силы T равна 7 sin 60°. Таким образом, форма уравнения проекции на ось z равна С = РА * + Рбз-П-пт Син 60°= 0.(?。） приступим к составлению уравнения момента для осей x, y и Z. Так как линии действия этих сил пересекают ось l, то силы RM » RAZt RBy и RBz на оси x будут равны пуле. Поэтому оси сил P и T. только момент относительно v не равен нулю. Сила P находится в плоскости, перпендикулярной оси l:.

От точки пересечения этой плоскости и оси x мы опускаем вертикальную ось EU вниз к линии действия силы P. момент силы P на оси x отрицателен. Это связано с тем, что из головы по оси Х видно, что сила Р стремится повернуть человека по часовой стрелке вокруг точки E. So … ТХ(р)= — п-ец. Сила T также находится на плоскости, перпендикулярной оси lg. Из точки N пересечения этой плоскости и оси L опускаем перпендикуляр NQ к линии действия силы T. момент силы T на оси x положителен. Средства мат)= Т-КЛ. (5）

Опишем уравнение моментов относительно оси x с учетом уравнений(4) и (5). Х «Л-М—П-ЕК-\ — Т-ПД =0.(6） при составлении уравнения моментов относительно оси y необходимо учитывать, что моменты сил RAy, RIiy и RAz равны нулю (сила RBy параллельна оси y, а линии действия сил RAy и RA2 пересекаются с этой осью).Поэтому момент, связанный с силовыми осями R RNZ и T, не равен нулю.

Сила P находится в плоскости, перпендикулярной оси Y. Из точки D пересечения этой плоскости с осью y опускаем вертикальный DC pa линии действия силы P. момент силы P на оси y Отрицательный ребенок. Из конца SSIy видно, что сила P стремится повернуть тело в точку[J по часовой стрелке. Средства ту(П)= — П-С. (7） момент силы на оси y РУз одинаково легко determine. In дело в том, что сила RBz находится в плоскости xz, перпендикулярной оси Y.

От точки А пересечения этой плоскости с осью y опустите перпендикуляр AB к линии действия силы RBZ. Момент положительный, так как с конца оси y видно, что сила Rnz стремится вращать тело против часовой стрелки вокруг эструса A. So … (LVL = ’ AB-(8） Поскольку сила T не находится в плоскости, перпендикулярной этой оси, то axis. it несколько сложно рассчитать момент силы T против y. So, сначала проецируем силу T на плоскость, проходящую через точку M, перпендикулярную оси Y. Проективная-это сила (помните, что проекция вектора на плоскость также является вектором).От точки o пересечения этой плоскости и оси y, сделайте вертикальную OM силой T {. к линии действия.

Момент силы T для оси y положителен, поскольку с конца оси y видно, что сила T1 стремится повернуть тело против часовой стрелки вокруг точки O. my (T)= 7, — ом. (9） Здесь мы используем уравнения (7), (8) и (9) для описания уравнения момента для оси Y. С / у,<ф) = — п-постоянного тока + РБГ. Ах + Тром = <к(10） осталось составить уравнение момента для оси Z. сразу заметим, что момент силы P, RAz, Rnz и Луча относительно оси z равен пуле(сила P, RA: RBZ параллельна оси z, а линия действия луча силы пересекается с этой осью).

Поэтому только моментом относительно оси z является сила Rpy и T. сила rBy находится в плоскости xy, перпендикулярной оси Z. От пересечения A этой плоскости и оси z опустите перпендикуляр AB к избыточному действию силы RBy. Поскольку конец оси z показывает, что сила RBy стремится повернуть тело по часовой стрелке вокруг точки A, этот момент отрицателен. / » , ( / ?».) = — Р » г АБ. (11） чтобы вычислить момент t силы на оси z, сначала найдите проекцию 7 \ 2 силы T на плоскость xy. Из точки А пересечения этой плоскости с осью z опускаем перпендикуляр AN к линии действия силы 7 \ 3. Силовой момент T на оси Z

Положительное значение. конец оси z указывает, что сила T *стремится повернуть тело вокруг точки A против часовой стрелки. Средства Т2 {т)= в(12） Далее опишем уравнение моментов относительно оси z с учетом уравнений(11) и (12). 2(ФК)= — Рой * ЛП + Т-I•в =0.(13） Итак, мы составили 5 уравнений(2), (3), (b), (10) и (13),

Чтобы определить 5 неизвестных лучей, раз, RBy, RBz и T. прежде чем приступить к решению этой системы, Сила Г и T. вычислите длину ее модуля и сегменты (плечи) EU, NQ, DC, АВ, ом, an Выражение（6）、（10）、（13）он может быть использован для 7 ^ =Гsin 30°=j-Т, 7 * =Гcos 30°= 7 *.Предположим, что буква А обозначает ширину полки. И затем… ПС =〜а> ШК =Л7Иsin 30°== грех 30°= а、 80-2 * 10 постоянного тока… J — 30 см.、 A B = 80-2•10 = 20 см, OL1 = 80-10 = 70 см, AN = OM = 70 см. Кроме того, условие P =■10 к G.

Система уравнений(2), (3), (b), (10)и (13) принимает вид: (14） Rai-RBM-10 + i-7 — = O, (15> — 10-А-Ф т. к.± — a = 0, (16） — 10.30 +/?E, — G0 + — i-7-70 = 0, (17） — *60 + g * 70 =0.(18） Осталось решить эти уравнения. Из Формулы (10)следует, что T = 10 кг. Замените значение этого T 5. В уравнениях (17)и (18) мы присваиваем:/ ^ = — ^ — =-0.83 кг, RBy-35 /- = Т-3 = 10,09 кг. Теперь из уравнений (14) и (15) подставим в них значения полученных RBy и RBZf, это будет выглядеть так: RAy= — = 5. = −1.44 кг1/?L,= 5^ -=: 5.83 кг, знак минус Rav и RBZ) указывают на то, что направление сил RAy и RBZ противоположны направлению, показанному на Рис.1 б.

Составляя уравнения моментов, мы столкнулись с некоторыми трудностями, поскольку при расчете силового момента T относительно осей y и z необходимо проектировать силу T в плоскости, перпендикулярной этим осям. Этих проблем можно избежать, ориентируя координатные оси y {и zx так, чтобы силовой момент T был равен нулю для них axes.

To сделайте это, возьмите начало координат в точке N и укажите оси вдоль оси x}и yy и z — {параллельно осям y и z соответственно (см. Рисунок B).Так как линии действия силы T пересекают эти оси, то легко видеть, что момент силы T{исчезает для осей yx и Z. Используйте координатные оси x, yy z {для создания уравнений равновесия для полок. Если уравнения (14), (15) и (16) не изменяются, то уравнения (17)и (18) принимают вид: 2 tU> = p * Cm-Yavg * DN-Raz•AN = 0, (19) 2 mtl(Fk)= RAy•AN-RBy. BN =0.(20）

Поскольку уравнения (19)и (20) не включают силу T, их легче построить, чем уравнения (17) и (18).Однако решение системы уравнений(14) до (18),（14）、（15）、（16）、（19） и (20) легче, чем решение. Таким образом, мы упростили создание уравнений моментов для оси y и оси zb, выбрав ось xy вместо оси x, оси y и оси z, но решение системы уравнений равновесия стало более сложным. Сумма расчета в обоих случаях практически одинакова.

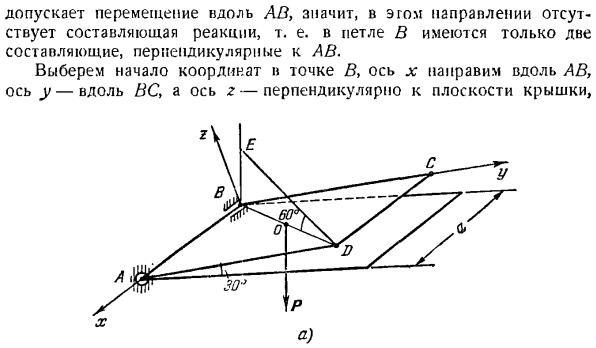
Задача 2.9.На рисунке показан грузовой люк с квадратной крышкой ABCD. Крышка крепится сферическим шарниром A и петлей (подшипником) B. После подъема крышки под углом 30°от горизонта она фиксируется с помощью направляющей линии DE, образующей угол 60°с плоскостью крышки. Шаровой шарнир и петли Б /опорной реакции и напряжения реакции определить. Вес крышки равен R. The solution. To определим неизвестные, рассмотрим равновесие покрытия ABCD. 1 активная сила приложена к крышке-ее вес P. приложите силу P точка O находится в центре квадратной крышки (рисунок B).

На крышке накладываются 3 соединения: шаровой шарнир а, стержень Б и линией де. Применяя закон освобождения, вы мысленно разрушаете эти связи, заменяя действия на обложке соответствующими реакциями. Разрезав Гильен Де в точке D, направьте отдачу Т от D К Е вдоль нее. Так как сферический шарнир а является неподвижной точкой, то нельзя сразу указать направление реакции, его необходимо заменить 3 компонентами, перпендикулярными друг другу.

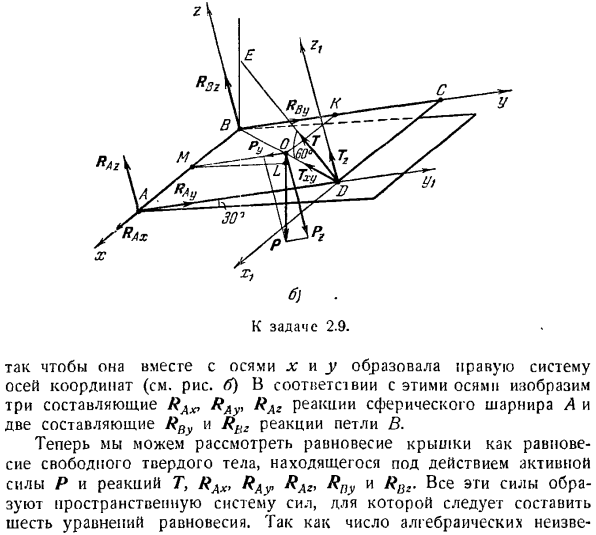
Цикл б Позволяет движение вдоль АВ. Это означает, что в этом направлении отсутствуют компоненты реакции. То есть, цикл B имеет только 2 компонента, которые перпендикулярны AB. Выберите начало координат точки B, ось x вдоль оси AB, ось y вдоль оси BC и ось z, перпендикулярную плоскости крышки. Д.） б.） К задаче 2.9. вместе с осями x и y мы формируем правильную систему координатных осей(см. Рисунок b).в соответствии с этими осями мы показываем 3 компонента реакции RAxi RAy, RA2 сферического соединения A и 2 компонента реакции петли B RBy и Rbz.

Теперь равновесие колпачка можно рассматривать как равновесие свободного твердого тела под действием активной силы Р и реакций 7, RAx, RAy RA2, Rny и всех сил. Эти силы образуют пространственную систему сил, в которой необходимо составить 6 уравнений равновесия. Число алгебраических неизвестных Скрытый момент пространственной системы сил относительно оси представляет собой сумму моментов всех сил системы относительно этой оси. С. С. С. ХХ = в rnx(ФК), ту = в ту(ФК), Р2 = в МЗ(ФК),(5 *） к = \ к = \ АР = 1 Иначе говоря н данные = 2, VkFhz-zkFky)у меня = ^- / Ф = 1/7 * я Ноги. «H = 2 {xkFhy-ykFkx). (6 *） Я… Знание основных пунктов системы

Он также равен 6 (Г, RXT RAv> RAZf RBV и RBz) и задача определяется статически. Когда уравнение равновесия построено, трудно учесть силу T, потому что вы не знаете угол, под которым эта сила образуется координатной осью x n y. таким образом, мы разложим силу T на 2 составляющие Txv и T2 так, что сила Txv находится в плоскости xy, а сила Tg перпендикулярна ей(см. Рисунок B), то есть параллельна оси z. Эти модули силы равны Thu = T cos 60°, Tg = T cos 30°. (1）

Проделайте то же самое с силой P и разбейте ее на составляющие Py и P2(сила P находится в плоскости, перпендикулярной оси L. So проекция на ось x равна нулю).Эти силовые модули включают в себя следующее: Ру = П грех 30°, Р2 = Р соѕ 30°. (2） С тех пор при создании уравнения равновесия, вместо проецирования силы T на ось, мы вычисляем сумму проекций силы Thu и T2 на эту ось, а вместо момента силы T на ось, мы вычисляем сумму сил Txv и момента T2 на соответствующую ось, основываясь на теореме валипера.

Создадим уравнение проекции сил на ось декартовой координаты. Силы Ru RAv> Raz, RBy> RBZ и T2 перпендикулярны оси x, а проекция на эту ось равна пуле. Поэтому только предсказания сил РАКС и Тху являются non-zero. So … X Fkx = Rax-дерево cos 45°= 0 Подставляя значение Txv из Формулы(1), получаем: £Fkx = RAx-Гcos 60° * cos 45°=0.(3） Поскольку силы Pzt RAKy, Rfiz и Tr перпендикулярны оси y и проекция на эту ось равна нулю, то в уравнении проекции на ось y находятся только силы RAy> RBv, Py и Txv. y-axis. So … £Pky = RAy-j-RBy-P sin 30° — Thu sin 45°= 0

Подставляя значение Чт из Формулы(1), получаем: V Fky = RAy + RI) y-Psin 30° — Tcos 60° — sin45э== 0.(4） Поскольку силы Pv, RAx, RAr RBv, Txv перпендикулярны оси z, и поэтому их проекции на эту ось равны пулям, то в уравнения проекции на ось z входят только проекции сил Pr, Tg, RAZ и RBz. £Fuz = RAz + RBZ-F cos 30°+ 7 cos 30°=0.(5） приступим к составлению уравнения момента для осей x, y и Z. Поскольку линии действия сил RAx, RAyt RA2, Rny, Rnz, Py и Txy пересекают ось x, моменты этих сил на оси x равны нулю.

Ненулевыми являются только силовые моменты P2 и T2. Сила Pr находится в плоскости, перпендикулярной оси lg. Эта плоскость пересекает ось x в точке M. отбросьте перпендикуляр MO из точки M на линию действия P2.Поскольку ясно, что сила P2 от конца оси l стремится повернуть тело по часовой стрелке вокруг точки M, момент силы отрицателен.

Следовательно, fn (P2)= — P2-Оуф. Если длина сторон квадратной крышки обозначается через a, a, то OM = aj <2.Принимая во внимание Формулу(2), запишем: mx (Pz)= — СПКЯ 30°. — (6） заметим, что для того, чтобы рассчитать момент P силы относительно оси x, не нужно разбирать силы Py и R-PPA на составляющие, первая из которых дает равный момент bullet. In фактически, сила P находится в плоскости, перпендикулярной оси X. от точки M пересечения оси x и этой плоскости опустите вертикальную ML к линии действия силы P. тогда mx (P)= — P * ML.

Из треугольника OML получаем: ML = OM cos 30°= cos 30°.Следовательно, mx (P)= = — П г в COS 30°.Соответствует формуле (6).Мощность P разложение Поскольку сила P не находится в плоскости, перпендикулярной этим осям, то при расчете моментов для осей y и r рекомендуется использовать компоненты Pv и Pr. Сила Tl находится в плоскости, перпендикулярной оси X.

Из точки А пересечения этой плоскости с осью х опускаем перпендикуляр AD = a к линии действия силы Tg. Момент положителен, так как сила Tg от конца оси x стремится вращаться вокруг точки A против часовой стрелки от arrow. So, mx (Tg)= Tg * a. учитывая формулу (I), она выглядит так: mx (Tg)= t sin 30° a. (7） Поэтому мы используем формулы ((>) и (7) для описания уравнения моментов относительно оси X. £tnx (Fh)= — Pcos30°•+Гcos 30°•а=0.(8） при создании уравнения моментов относительно оси y линия действия силы RAx/?Следует учитывать, что R » RBzy Thu пересекает ось y, а линии действия сил RAy и Пу параллельны оси Y.

Таким образом, момент всех этих сил на оси y равен нулю. Это означает, что в уравнение момента на оси y вводится только сила: раз)ПР и тр. Сила раз находится вокруг плоскости xz, перпендикулярной оси Y. От этой плоскости и пересечения оси y B мы опускаем перпендикулярную линию B A = a к линии влияния RAz. Момент раз отрицательный. Это связано с тем, что с конца оси y вы можете видеть, что сила RLr стремится вращать тело по часовой стрелке вокруг точки B. означает мой (раз)= — рас-а. (9）

Сила Pr находится в плоскости, перпендикулярной оси Y. От точки пересечения этой плоскости и оси YK мы опускаем вертикальную линию KO-y к линии действия Pr. конец оси y указывает на то, что сила P стремится повернуть тело против часовой стрелки вокруг точки K, поэтому момент положителен. Поэтому rny (Pz)= Pr•y. Если рассматривать Формулу (1), то она выглядит так: ту(П)= Р соз 30° — г (10） Сила Tz находится в плоскости, перпендикулярной оси Y. Опустить вертикальную линию от точки пересечения C этой плоскости и оси

После использования уравнений (9), (10) и (II) уравнения моментов относительно оси y принимают вид: £tu (Fk)= — RAz * а-fPcos 30°• — Tcos 30°•а=0.(12） осталось составить уравнение момента для оси Z. Силы RAx, RPy) заметим, что рабочие линии RBz и Thu пересекают ось z, а силы R / U, Pr и T2 параллельны этой оси. Таким образом, момент этих сил относительно оси Z будет равен пулю.

Это означает, что в уравнение моментов входят только моменты 2 сил: Ru и RAy. Силы Py и RAy находятся в плоскости xy, перпендикулярной оси Z. от пересечения B плоскости xy и оси z опустите перпендикуляр BM = a / 2 к линии действия Ru, а перпендикуляр VL = a к линии действия луча. Момент силы ру отрицательный, а Луч положительный.

Это происходит потому, что от края оси z сила Ru стремится повернуть тело по часовой стрелке вокруг точки B, а сила Луча поворачивается против часовой стрелки. Средства м *(Вау)=Куруа> 03） м2(ру)= — Пы -} = — П Син 30°.(14) (результат (2) рассматривается в Формуле (14).） Используется для описания потери моментов относительно оси z Формулы (13)и (14）： = в Sin 30°.- /=0.(15） Итак, уравнение равновесия покрытия принимает вид: в ГХ = Ракс-Т cos60e * в COS 45°= 0, (3） £Fhy = RAy + RBy-P sin 30° — T cos 60° * sin 45°= 0, (4） X Fhz = RA2 + RBz-P cos 30°+ T cos 30°= 0,(5） £МХ(ФК)= — П соѕ 30°• — 4-Т соѕ 30°•А = РР 0,(8） ^ / я> (=- раз. a + P cos 30° * y-Tcos 30°•a = 0, (12） Х МЗ(ФК)= РА-а-п грех 30° » — =0.(15）

Осталось решить эту систему из 6 уравнений с 6 неизвестными, определить неизвестные. Из уравнений (8) и(15)найдите T и RAy напрямую, добавьте уравнения(8)и (12), чтобы получить RAr. Затем вычислите RAx из (3) и вычислите его из (4)-RBy и (5)-Rlis. П Р В 2 Дайте ответ: T = y, RAy= -, RAz = 0, R / lX = ~~ P = = 0,18 P, RBy = P■ — = 0,43 P, RBZ = ^ P = 0,4 3 P Если при решении задачи трудно рассчитать момент для оси силы, то достаточно выбрать начало координат на линии действия этой силы, чтобы эта сила не вошла в момент equation. So, для того чтобы сила T не входила в уравнение моментов этой задачи, достаточно взять начало координат в точке приложения D силы 7 \и оси X\, y\, Z\, и направить ее параллельно оси x, y, z\, respectively.

In в этом случае уравнения проекции на оси xv и Z1 решаются с использованием jc, y и уравнений проекции на оси Z.（3）、（4）、（5） формат совпадает с форматом файла. Так как линии действия силы T пересекают оси xi y \и zJt, то эта сила не входит в соответствующий момент equation. So … Год.>»(ФК)=-раз■а-РНЗ•а—п соѕ 30°•= 0, (16) Спайк в(ФК) = РНЗ * я-п, потому что 30 «•\ = 0, (17） ZmZl (Fk) = P sin 30’.？Т + Ракс. а-моего-а = 0.(18） Теперь, чтобы определить неизвестные, нам нужна система уравнений（3）、（4）、（5）、（16）、（17）、（18）вы должны решить головоломки. Сложность составления уравнений моментов (8), (12) и (15) и уравнений моментов (IG), (17) и (18) для осей x, 2 \практически одинаковы.

Система уравнений(3), (4), (о), (8), (12) и (15)и система（3）、（4）、（5）、（16）、（17）сумма расчета (18) почти одинакова. Если в состоянии этой задачи петля B заменяется сферическим шарниром, то в точке B добавляется алгебраически неизвестная компонента реакции RBxt, существует 7 (RAx, RAy * RAz> RBx, R [iyt Rlu и T), и задача статистически не определена. Если одновременно с введением сферического шарнира B направляющая линия DE заменяется известной силой T по величине и направлению, неизвестное становится 6 (RAx, Ra> «Клг> RB >ялзадача остается статически неопределенной).- Noah.

In факт, выбрав предыдущие направления x, y и осей, нетрудно подтвердить, что RAx и RDx являются недействительными только с 1 из 6 уравнений равновесия-в этом случае уравнение проекции на ось x *(3) является тем же самым.） £Fbx = RAx + RBX-T cos 60°•cos 45°= 0. Из этой формулы мы можем только определить сумму RAX RBx, но мы не можем найти каждую из этих неизвестных. Это подтверждает сделанное в обзоре теории этой точки указание на то, что задача о равновесии твердого тела с 2 неподвижными точками (в данном случае 2 сферическими шарнирами) не определяется статически.

Учитывая тот факт, что решение задачи 2.7-2.9 дает подробное описание методики составления уравнений равновесия, в следующих 2 задачах эти уравнения составляются без дополнительных пояснений. Задача 2. 10.На этом рисунке показан поворотный круг с упорным подшипником а и подшипником в, которые имеют 2 опоры на оси вращения. При помощи троса, переброшенного через блок D, груз е подвешивается на конце троса при повороте крана вокруг оси AB. Вес сетки, приложенной к центроиду C, равен PX = 2T.

вес поднимаемого груза E равен Pi = 4T. конструкция крана совмещена с плоскостью чертежа. То есть, на самолете YZ. ось X направлена к нам. В точке подключения к кабеля для крана, ось xvyuZi рисуется параллельно осям X, Y и Z, соответственно. Наклонная ветвь кабеля образует горизонтальную плоскость jc, Vi и угол 60°.Это ветеринарная проекция

Начало координат тела O и его направляющий Косинус по выражению： Я Т01 == ДМС + мл + мл(7 *） соѕ(х? М0)= ^ Т, потому что(г? МО)= ^] Т, потому что(я? М0)= ^ — Р(8 *） Согласно теореме Варпиньона, если пространственная система сил сводится к равнодействующей силе, то момент равнодействующей силы против точки определяется векторной суммой моментов всех сил системы против одной и той же точки. н.

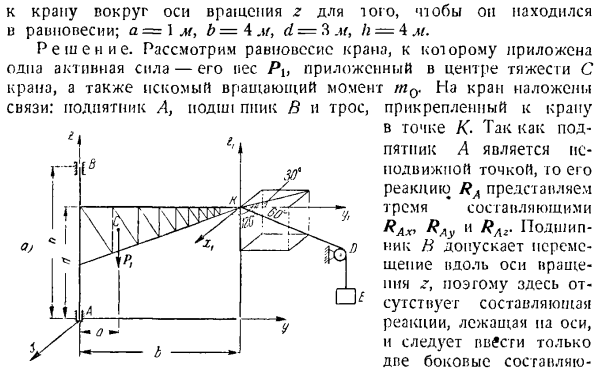
Та же теорема по оси декартовых координат формулируется следующим образом: момент Объединенных сил относительно оси равен сумме моментов составляющих сил относительно той же оси. С. С. С. МХ?) =тmx (Fk), niy^®= V, Пуη (FK), η ^®= VM, (FK). К. ул к = л {я К крапиве вокруг естественного вокруг вращения z, так что состояние равновесия. а = 1 м, B = 4 м, д = 3 м,/ г-4 и/. Решение. Рассмотрим равновесие крана, в котором приложена 1 активная сила-ее нес ПЛТ, приложенный к центроиду С.

Кран, а также желаемое Поворотное соединение: упорный подшипник а, узел ППК Б、 Момент t0.Трос крепится к крану и крепится к колену с точкой К. Поскольку упорный подшипник а является неподвижной точкой, то его отдача RA представлена 3 компонентами RAhu RLu и RLg. Поскольку подшипник B можно перемещать вдоль оси вращения z, на оси нет компонента реакции, необходимо ввести только 2 боковых компонента- И RBx, и RBy.

После отсоединения кабеля вблизи точки подключения K направьте реакцию T вдоль кабеля. Здесь вместо силы T часто возникает большая ошибка, которая прикладывается в точке E и представляет собой вес Pi вертикально нисходящей нагрузки E. мысленный анализ троса вблизи точки крепления K и\ T \ = Po | = 47’.Под действием вращения Момент t0 и сила: PRAx, RAyt RA2y RBx, nBy Неизвестными являются 6 (RAx, RAy RA2} RBxi RBy и mQ) t, задачи определяются статически. К выпуску 2.10. Так… К кабелю. Е из состояния равновесия груза теперь рассмотрим равновесие крана Р ЛЧ » РЖ Т.

Поскольку построение уравнения равновесия осложняется пространственным расположением силы Tu, сначала разложим силу T на 3 составляющие, Tx, Tu, 7\, параллельные осям x, y и r. bo0. (1） Р. Tu = древесина cos 30°= T cos 60°cos 30° Используя (1), Вы можете увидеть следующее: ТХ = 1 ТТ Ту = Г «3 Т ТГ = 2 В 3 Г.(2） Далее мы создадим уравнение равновесия для крана. X Т = ^ ЛК -’Р ^ ПХ-ТХ = 0т£Fby = Луч-rRny» ч 1 г- 2-Раз Тг-О、 (о） В МХ(ФК)= — П] а-Rjiyh -/ / — = 0, Zlmy(ФК) = RBxli-на TXD = 0、

При решении системы, принимая во внимание не только числовые данные, но и значения 7’l и (2) T2, можно увидеть следующее: = 4 7 «ll = 0.75 7», RBy = = −5.31 T、 RAx = 0,25 Г, RAy = 3,58 7″, = 5,40 Т. Предположим, что условие для этой проблемы изменилось. Указанный целевой крутящий момент М0-это и есть упорный подшипник, а не подшипник Б. Потом в точке Б, неизвестный компонент ПК-acin Ри; добавил Z-это.

Число алгебраических неизвестных остается равным числу уравнений, т. е. 6 (RAx, RAy, RAz, RIix, RBv, RBz), но фиксированная задача оказалась статически indefinite. In факт, раз и РЛу вводят только уравнения проекции на ось Z. £Гиг= — Раз-Г «РН * — Пы〜Т * = Из этого уравнения можно определить только сумму RA: Rl> Zi, и каждое из этих неизвестных невозможно. Полученные результаты подтверждают сделанное в обзоре теории этой точки утверждение о том, что задача о равновесии твердого тела с 2 неподвижными точками (в данном случае скольжения а и в) не определяется статически, несмотря на соответствие числа вопросов и числа уравнений.

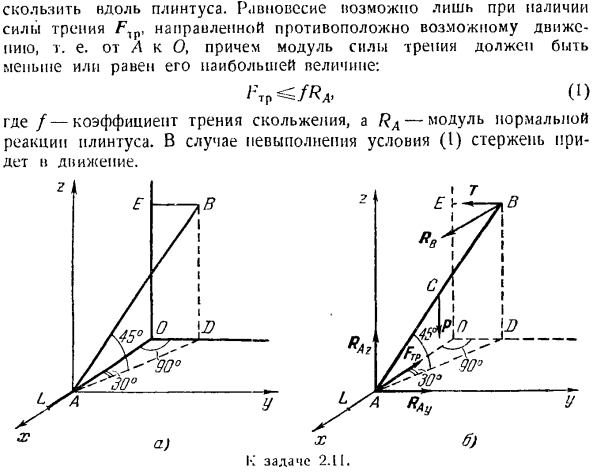
Задача 2.11. однородный стержень АВ массой Р, образующий угол ИОЛ и 45°, является касательным к плинтусу, где конец а не является гладким в помещении(рисунок а), а конец В является касательным к гладкой вертикали wall. At в точке B к стержню крепится горизонтальный кабель. Проверьте, может ли стержень поддерживать состояние равновесия, если коэффициент трения скольжения на плинтусе равен/ = 0,5, а угол наклона акционерного общества равен 30°, также определите реакцию плинтуса, стенки и троса. оси X, Y и Z показаны на рисунке. Решение.

Если плинтус гладкий, он не может держать ядро balance. In в этом случае конец стержня а начинается Скольжение вдоль плинтуса. Равновесие возможно только при наличии силы трения FJ? Она направлена в противоположную сторону от возможного движения, то есть от L до O, и модуль силы трения должен быть меньше или равен максимальному значению： 0.） Где/ — коэффициент трения скольжения, а RA-нормальный коэффициент реакции плинтуса. Если условие (I) не выполняется, стержень перемещается.

Выпуск 2.11.To. 1 к ВВС прилагается активная сила-ее масса P (рисунок B).Благодаря условию, стенка гладкая, поэтому ее отдача RB перпендикулярна плоскости стенки, то есть параллельна оси X. Сила реакции кабеля T направлена от B к E. каково направление силы трения F1?Об этом говорилось выше.

Нормальная реакция плинтуса RA на плоскость yzj в направлении, которое еще не известно. Таким образом, мы разбиваем силу RA на 2 взаимно перпендикулярные компоненты RAy и RAz. 00. Иначе говоря Задача определяется статически. Неизвестное число — 5.Р.

Под действием вращения Момент t0 и сила: PRAx, RAyt RA2y RBx, nBy Неизвестными являются 6 (RAx, RAy RA2} RBxi RBy и mQ) t, задачи определяются статически. К выпуску 2.10. Так… К кабелю. Е из состояния равновесия груза теперь рассмотрим равновесие крана Р ЛЧ » РЖ Т. Поскольку построение уравнения равновесия осложняется пространственным расположением силы Tu, сначала разложим силу T на 3 составляющие, Tx, Tu, 7\, параллельные осям x, y и r. bo0. (1） Р. Tu = древесина cos 30°= T cos 60°cos 30° Используя (1), Вы можете увидеть следующее: ТХ = 1 ТТ Ту = Г «3 Т ТГ = 2 В 3 Г.(2） Далее мы создадим уравнение равновесия для крана.

X Т = ^ ЛК -’Р ^ ПХ-ТХ = 0т£Fby = Луч-rRny» ч 1 г- 2-Раз Тг-О、 (о） В МХ(ФК)= — П] а-Rjiyh -/ / — = 0, Zlmy(ФК) = RBxli-на TXD = 0、 При решении системы, принимая во внимание не только числовые данные, но и значения 7’l и (2) T2, можно увидеть следующее: = 4 7 «ll = 0.75 7», RBy = = −5.31 T、 RAx = 0,25 Г, RAy = 3,58 7″, = 5,40 Т. Предположим, что условие для этой проблемы изменилось.

Указанный целевой крутящий момент М0-это и есть упорный подшипник, а не подшипник Б. Потом в точке Б, неизвестный компонент ПК-acin Ри; добавил Z-это. Число алгебраических неизвестных остается равным числу уравнений, т. е. 6 (RAx, RAy, RAz, RIix, RBv, RBz), но фиксированная задача оказалась статически indefinite. In факт, раз и РЛу вводят только уравнения проекции на ось Z. £Гиг= — Раз-Г «РН * — Пы〜Т * =

Из этого уравнения можно определить только сумму RA: Rl> Zi, и каждое из этих неизвестных невозможно. Полученные результаты подтверждают сделанное в обзоре теории этой точки утверждение о том, что задача о равновесии твердого тела с 2 неподвижными точками (в данном случае скольжения а и в) не определяется статически, несмотря на соответствие числа вопросов и числа уравнений.

Решение. Если плинтус гладкий, он не может держать ядро balance. In в этом случае конец стержня а начинается Скольжение вдоль плинтуса. Равновесие возможно только при наличии силы трения FJ? Она направлена в противоположную сторону от возможного движения, то есть от L до O, и модуль силы трения должен быть меньше или равен максимальному значению： 0.） Где/ — коэффициент трения скольжения, а RA-нормальный коэффициент реакции плинтуса.

Если условие (I) не выполняется, стержень перемещается. Выпуск 2.11.To. 1 к ВВС прилагается активная сила-ее масса P (рисунок B).Благодаря условию, стенка гладкая, поэтому ее отдача RB перпендикулярна плоскости стенки, то есть параллельна оси X. Сила реакции кабеля T направлена от B к E. каково направление силы трения F1?Об этом говорилось выше.

Решая систему уравнений(3) — (7), вы найдете раз из (О), Т из (6), РБ из (7).Затем вы получаете h \ p из(3) и RAy из (4).Таким образом, искомая сила равна модулю / ?, = P, Луч-7 = 0,25 P,/?= Фтп = ^ п — = 0.43 п. (8） Необходимо проверить, может ли стержень поддерживать состояние равновесия. В соответствии с Формулой (2) запишем: РА = ВФ? АУ + Р \ З (9）

Вводя значения RAy и RAz из (8) в уравнение (9), мы видим, что: \ GU1 = 1.04 п.(10） Подставим значения f и R для неравенств (1), (8) и (10), и если f = 0.5, то получим: 0.43 / > <0.52 I. Поскольку условие (1) выполнено, стержень находится в равновесии. В заключение рассчитывают минимальное значение коэффициента трения скольжения/при котором стержень сохраняет свое равновесное состояние.

Если отбросить инфинитив Формулы (1), то найдем следующее: f—0 41 ДЖ-Р-1.04 П〜 Один. Если коэффициент трения скольжения меньше 0,41, стержень не сможет поддерживать состояние равновесия и начнет двигаться. Начиная с 1950 года И. В. Мещерским из «сборника задач теоретической механики» рекомендуется решать следующие задачи:246、254、257、262、264、265、267、268、271、272、276、 277、278。

3°. Чтобы придать любому пространству системы 5-й силы простейшую форму, рекомендуется выполнять ее в следующем порядке: 1) Выберите ось декартовых координат. 2) взять центр редукции системы сил в начале координат О. 3) вычислить главный вектор v проекции VXf Vv, Vz системы сил по формуле (9*). 4) определить модуль главного вектора V и направление косинусов по формулам (10 *) и (11). V = Vxi + Vyj + Kk; 5) найти основные моменты mx, myt m, систему сил относительно осей x, y, z, но по формуле (5), (6 ）; в) по формулам (7) и (H*) определить абсолютное значение основного момента m0 и его индуцированного Косинуса.

М0 = МЮ + myj + МЗК \ 7) найти простейшую форму, которая дана системе власти данной. а) в случае V = 0 и m0 = 0 твердое состояние, к которому приложена система данной силы, находится в равновесии. Б)если V = 0,0, то система сил сводится к паре сил с моментами m0. в)Если V ^ 0, m0 = 0, то система сил уменьшается до R = V result. In в этом случае уравнение результирующей линии действия выглядит следующим образом:

Где Ud, Vy, Vz-проекции основного вектора V, определенного в пункте 3, а x, y, z-текущие координаты результирующей линии действия. г) Если V-7> 0, m0 <0, то необходимо проверить, перпендикулярны ли V и m0 друг другу. Для взаимной перпендикулярности V и т0 их скалярное произведение Vtn0 равно нулю. Поэтому необходимо проверить, соответствует ли равенство Vxmx — \ — Vymy — \ — Oct2 = 0

Момент пары сил в пространстве определяется как вектор, перпендикулярный к плоскости пары и отображается по часовой стрелке от края, что пара(рис. 2.8).Данный момент модуль Пара сил равна произведению расстояния (плеча) между двумя модулями силы и линией действия силы пары:\ m \ — Fh. Теория пар в пространстве задается 2 теоремами. Теорема 1.Равные пары векторных моментов эквивалентны. Таким образом, пара сил может передаваться на плоскость, параллельную этой плоскости, не нарушая твердого состояния. Теорема 2.Результирующий парный момент равен векторной сумме составляющих парных моментов.

Для равновесия твердых тел под действием пар сил в пространстве необходим и достаточен вектор н. Сумма моментов этих пар равнялась нулю (V mk = 0). В. Здж. Расчет основных моментов системы моментов и сил сил касается следующего: это важный элемент, решающий задачу о равновесии твердых тел под действием любого пространства. ^ Я х Т Рисунок 2.8.

Когда равенства выполняются, система сил уменьшается до R результата. Уравнение действия R в результате в этом случае имеет вид: МЗ-xVy — \ — yVx ВЗ Илли-zVx — \ — ху. зет. _ (16 *） Если vxmx -) — •Vymy-j-Vzmz = 0 не выполняется, то главный вектор V и главный момент m0 не перпендикулярны друг другу, и система сил уменьшается до Динамо.

Уравнение центральной оси также определяется по формуле(16*). V основной вектор динамо-машины определен в 4-м абзаце. Основная точка уменьшительного Центра дивам, взятая вдоль центральной оси, находится на этой оси. Проекция на центральную ось (минимальный момент) является выражением Если пространственная система сил сведена к простейшему виду, то ось декартовых координат следует выбирать так, чтобы максимально возможное число сил было параллельно или перпендикулярно этим ЧХ ’ ЛК-я-VyMy + ВЗ™. В. Оси и мобы линии действия сил максимально пересекали эти координатные оси. Задача 2. 12.

Пространственная система сил была направлена к центру O, взятому в начале координат xyz system. In в результате редукции были получены следующие результаты: мощность V = \ 0k и силовые пары, вектор которых равен простому моменту системы tn0 = 12i — [- 20ft, даже [//=i, и [/i0] = j. Если точка A находится на оси y на расстоянии OA = 2m от начала координат, причем точка A является центром редукции, то определенная силовая система определяет пару приведенных сил и усилий. Решение. Если вы хотите уменьшить силу космической системы

в i-м Центре сила равна основному вектору V, А главный момент изменяется по формуле. = М0 + abhc0. (1） Поэтому построим силу V в точке A. затем переместим m0 в точку A и нарисуем момент, то есть mA (V0), относительно нового центра A силы Vy, приложенной к старому центру O. поскольку ntA (V0)нужно направить перпендикулярно плоскости, проходящей через V0 и точку A、 То есть для плоскости y2 вектор ma (Vq) параллелен оси и направлен в противоположную сторону (рисунок a), так что сила V0 с ее конца выглядит»против часовой стрелки вокруг центра A».

кроме того, / тА (v0)/ | / V \ OA = 20 J. В. Вт>/ К ДЖ / А (ФБ)> РНВ = х U(ФК)> с mzifk）- k = \ k = I k = 1 Введение обозначения: OB = OS = a, для данной системы сил： т— и 1/3 s c A V3 tg = 0. Принимая во внимание условие (1), опишите в виде (2) — © — F, cos 60° + cos 45°= 0、 — Потому что Альфа 60°+ / — 8 в COS 45°= 0, Фи Косинус 30°+ Фо соѕ 30° — Ф3-ФА = 0、 Условие находит Fz = Fa =Fb-из формул (11) и (12), так как F1 = / 74 = β, а формула (8) дает Fb = F-tr. So …

Эти H3, Z7 и значения формул (9) и (10) исчезают точно таким же образом. Таким образом, энергетическая пирамида находится в равновесии под действием следующих 5 энергетических систем: Ф r_r. Ва п р. Г_- Задача 2. 14. Чтобы сделать силовую систему Fb Ft> F3 простейшей формой, мы применяем Fa и F6 к вершинам C, B и E Куба, где ребра a. Ft = Fi = F3 = Fi = F; Ф9 = Ф6 = Ф] / 2.Направление действия силы показано на рисунке. один. Решение. Укажите ось y, z вдоль края куба, с точкой O в качестве центра сокращения (рисунок A).Определяет проекцию Vx, Vy, Vz Vx главного вектора V на оси X, y, z = ZFkx = F, — Fs cos 45°、

С — J — / * * ов соз 45° — Джей-Ф6 Косинус 45°, В= с = ОС-соѕ 45° Заменяя значения модулей этих сил, получаем: ЧХ = вы = в = о Таким образом, главный вектор V системы сил равен нулю. Приступим к определению основного момента m0.Сначала найдите основные точки системы сил на осях x, y, z m. ТХ = в Техас (ФК)= Fza-Фау соз 45°-F6a грех 45°、

моя = 2 Мой(ФК)=—Ф * значение COS 450 + в COS 45°> = £МЗ(ФК)= — РГА-ФКА F6a соз 45° — (- F8а грех 45°.Подставляя значения коэффициентов этих сил, получаем: МХ = — ФА, ту = — Ра, м2 = 0 Таким образом, основной момент m0 = — Fai-FaJt и его модуль m0 = + My + mz = Fay2. Система полномочий и задачи, которые делают эти системы власти простейшей формой. Следующая процедура рекомендует расчет основного момента силовой системы относительно оси.

1) Нарисуйте плоскость, перпендикулярную оси. Для этой плоскости определите главный момент системы сил. 2) найти пересечение этой плоскости с осью. 3) расчетные усилия на плоскости, перпендикулярной оси. 4) опустить перпендикуляр (плечо) от пересечения оси и плоскости на линию действия проекции сил на плоскость, определенную в предыдущем пункте. 5) напишите модуль момента силы против оси, в виде произведения модуля проекции силы на плечо найденного.

6) определите знак момента силы относительно оси. 7) для каждой силы системы повторите построение и расчеты, выполненные в 3-й, 4-й, 5-й и 6-й точках. 8) вычислить основные моменты системы сил относительно оси, в виде суммы моментов этих сил относительно этих осей. Если трудно определить проекцию силы на плоскость, перпендикулярную оси, то силу необходимо разложить на составляющие. Затем, вместо момента силы относительно оси, нужно рассчитать сумму моментов сил, которые составлены для этой оси, используя гео-теорему бариньона.

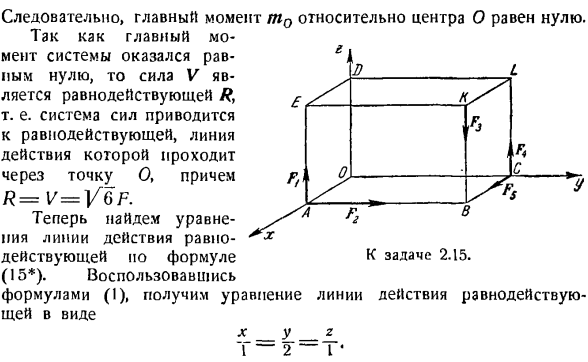
Таким образом, получается, что эта система сил сводится к паре сил с силой V = 0 и моментом m0 =-Fai — Fa/. b (пара сил находится в плоскости, перпендикулярной т0, поэтому пара с конца т0 выглядит против часовой стрелки). Задача 2. 15.In для того чтобы придать простейшую форму, система сил Flt Fit F»f4 и FB приложена к вершинам прямоугольников A, K, C Параллелепипед OBCDEKL; ФЛ = ФЗ = Fп = FВ = FТ Ф ^ = = 2Ф, ОС = а, ОА = Адж 2. Решение.

Определить проекцию основного вектора V на оси x, y, z Vxt Vy, Vz, с точкой O в качестве центра редукции. ЧХ = JLFkx = Р * вый = 2Fky = Ф * ВЗ = ZFlu = ФЛ-м-\ — Фут. Подставляя значение модуля силы, он выглядит так: ЧХ = Ф уу = 2Ф, ВЗ = Ф.(1） Таким образом, основной вектор V = Fi 2Fj + Fk>и его модули V = Vvi + V} + VI = / / 6 F. Найдите здесь основные точки системы этой силы для осей x, y, z: mx, m} tnz. МХ = ФКА, ту = Ф ^ — Форекс м, МЗ = ф%ф— ^ а、 Или, подставляя значение модуля силы, выглядит так: т к = 0, Т= 0,Т » = 0.

В результате главный момент m0 для центра O равен нулю. Так как основной момент системы оказался равным нулю, то сила V есть самость результата. То есть система сил сводится к результату, линия действия которого проходит через точку O、 R = V = VGF. Теперь найдем уравнение линии действия, вытекающее из Формулы (15*).Используя формулу(1), получим следующее уравнение: Х _ у _ з Г Д Л > / Ля 0 * Ф4 С Y * К задаче 2. 15. Г.

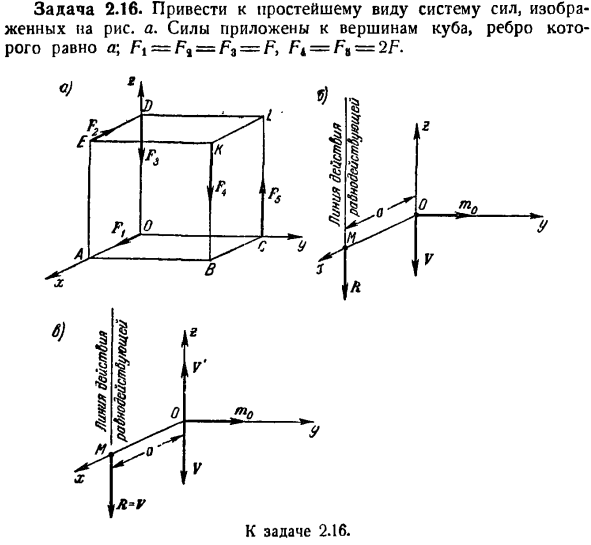
Результатов действий Задача 2. 16.In для того чтобы сделать систему сил, описанную на рисунке 1, простейшей формой. Сила, край — это \ Fi = Fa =beta?= F, применяется к вершинам Куба, равным Fi = Fv = 2F. Решение. На диаграмме показаны оси декартовых координат x, yt z, с точкой O в качестве центра редукции. a. определите проекцию V * Vy Vg главного вектора V на оси x, y и g. = Вы = 2Fky = 0, ЧХ = ЗФ ** = e_F.- Интернет + Ф..

Заменяя значения модулей этих сил, получаем: 1 ^ = 0, 1 / г = 0, В2 = — Ф(1） Происхождение основного вектора В = — Фкт(2） И его модуль K = VV’X + V} + VI = F(3） Главный момент системы сил на оси x, yy-z определяет t # tuy-tg. mx = 2хχ(γk)= — + F ^ a、 ffty =туЛЛ) = — F, A + Fr = тm2 (FK) =0 Подставляя значения модуля этих сил, получаем: ТХ = 0, = мое ТВС, Т2 =0.(4）

В результате главный момент для центра O М0 = ФА] г(Б） И его модуль / «O = Vmi + m’y + ml = Fa. (6） В соответствии с формулами (2) и (5) на рисунке показан основной момент m0 силы V и силовой системы. Получается, что V и т0 взаимно перпендикулярны, поэтому систему сил можно свести к результату R и даже к R = v. используя формулу (1) и (4), запишем (16*) в следующем виде: у Х 0

откуда x = a, y = 0, то есть линия действия результирующего R =-Fk находится в плоскости XZ, параллельной оси z и с интервалом X-a (рисунок b). Положение линии действия результирующего R можно определить без использования формулы (7).На рисунке c показан основной момент rttQ, приложенный к силе O и точке O. поскольку основной момент m0 находится на оси y, пара сил, соответствующих основному моменту m0, находится на плоскости, перпендикулярной m0, или плоскости xz. с конца m0 пара выглядит против часовой стрелки.1 из сил V, составляющих пару, притягиваются к противоположной стороне V, V » = — V.

Тогда линия действия 2-й силы V, входящей в состав пары сил, должна быть отделена от линии действия 1-й силы на расстоянии= так М0 = Альфа, в = Ф>, ОМ = А, и т. д. Таким образом, получается, что система сил уменьшается до 3 сил: силы V и V’, приложенные к точке O, силы V, приложенные к точке M. первые 2 силы уравновешиваются и могут быть разрушены. Таким образом, система сил сводится к 1 силе V, которая приложена в точке M.

следовательно, результат равен R. линия действия полученного R параллельна оси z, а расстояние от ол равно a1 = a (рисунок I). Следует иметь в виду, что общим методом определения уравнения линии действия результирующего R является использование формулы (7). Задача 2.17.Для простейшей формы на диаграмме показана система, состоящая из 2 пересекающихся сил T7 и A \ 2. a; Fi = F%= F, OL = a. сила параллельна оси Ox. По заданию 2.17. Решение.

Определите проекцию Vx> Vv, Vz главного вектора V на ось x yy z, точно так же, как вы решали предыдущую задачу, с точкой O в качестве центра редукции. В» = 2 = ФБ вы■ ■ = 2Fky = 0, В2 =%ФКЗ = — ФЛ. (1) | Ft \ = / F ^ / = / мы имеем： VX = F, Vy = 0, Vz = — F. (2） Поэтому главный вектор В = ФИ-ФК(3） И его модуль В = ВВ \ + В $ + Ви = Ф П2. (4） Найдите здесь основные моменты системы сил относительно оси y, z, mx, mv, mr.

МХ =£МХ(ФК)= 0, моего =£М(ФК)= 0、 =% МЗ(ФК)=-/ х . (5） Так как= то МХ = 0, −0, г = — ФА. (6） Так что суть т0—Фак (7） И его модуль = — г мл = ФА. (8） Поэтому система скрещивающих сил сводится к тому, что показано на рисунке. сила V = Fi-Fk и пара сил, момент которых равен основному моменту для центра O, т. е. m0 = — Fak. В этом случае отсутствие перпендикулярности векторов V и τ0 очевидно. Для более сложных задач можно использовать скалярное произведение Vm0 = Vxmx〜Vymy + V2mZt.

Это должна быть пуля, если векторы V и т0 перпендикулярны друг другу other. In вопрос, мы используем Формулы (2) и (6), чтобы получить Vm0-F ^ a. следовательно, векторы V и τ0 не перпендикулярны друг другу. Это означает, что система сил сводится к глубинам. Найти уравнение центральной оси по уравнению (IG).Формула в этом случае, учитывая Формулы (2) и (b), принимает вид: Таким образом, центральная ось лежит параллельно плоскости, параллельной координатной плоскости xz, а расстояние a / 2 параллельно биссектрисе MN только врозь.

Осталось определить главный момент m относительно центра торможения, который находится на центральном axis. As известно, что вектор m находится на центральной оси. Проекция в направлении главного вектора определяется по формуле (17). Используя равенство (2), (4) и (6), получаем следующее: (-0） Основной момент m показан на рисунке. с. Итак, получается, что эта система пересекающихся сил сводится к Динамо, то есть силе V = Fi-Fk, и паре сил, которые расположены в плоскости, перпендикулярной V. проекция этой пары моментов m

Если этот прием также сложен, то нужно найти проекцию силы Fx% F: y 1: r на ось, описать координаты x, y> z точки приложения силы и вычислить момент силы на оси декартовой координаты по формуле (-3). Если ось декартовых координат не задана в состоянии задачи, то рекомендуется выбрать эти оси так, чтобы момент максимального количества сил исчез. Это означает, что ось должна быть направлена параллельно силе или ось должна пересекаться с линией действия силы.

Задача 2.4. если длина ребра, параллельного оси x, равна a, вычислите моменты для осей x, y и z силы F, которая направлена наклонно в сторону прямоугольной коробки, показанной на рисунке. Решение. Так как линия действия силы F пересекается с осью x, то момент силы F к оси x равен нулю. МХ(ф)= 0. чтобы определить момент силы F относительно оси y, эта сила проецируется на плоскость xzy, перпендикулярную оси Y. y-axis. In другими словами, вы определяете Fxz. Легко видеть, что FXS = F cos 30°. осталось получить данные момент силы относительно точки о пересечения оси с перпендикулярной плоскости узнать. Плечо-это край.

Направление основного вектора V (минимальный момент) определяется по формуле (10). Эту задачу можно решить с помощью простой конструкции, минуя проекцию. Дайте заданные силы f и Fb, которые изображены на рисунке, и доведите их до 1 Центра. Теперь, когда мы выбрали точку приложения силы Fb в качестве центра торможения, мы построим 2 равновесн

ые силы в точках A и FJ. Сила V рассчитывается как сумма сил Fx и Fb, приложенных к точке A. FTM. При равенстве модуль силы V= FV2(в этом Для параллелограмма силы она превращается в квадрат, параллельный плоскости xz, а сила V параллельна биссектрисе (млн). Когда сила Fx перемещается к центру A

, она добавляет пару к конфигурации силы F, приложенной в точке F, и силы F, приложенной в точке O. плечо пары OA является a(рисунок D).Так как объединенная пара сил находится в плоскости yz, то момент этой пары (главный момент mA) направлен перпендикулярно плоскости yzy, то есть параллельно оси X. Modiolo: ма = ФА. Разбейте главный момент Ма на 2 составляющие. ма= м + м. Где вектор m соответствует направлению основного вектора V, а mx перпендикулярен основному вектору. Мы видим, что параллелограмм момента (в данном случае квадрат)также находится в плоскости, параллельной плоскости xz. Мы это выясним： МХ = м = Май = мой Вектор M не зависит от выбора центра снижения. От вектора, перпендикулярного силе V,

для этого можно перейти к новому центру торможения и избавиться, построив пару сил, соответствующих моменту mv.1 из сил, которые входят в пару, представлены в V и направлены с силой V, чтобы они были сбалансированы. Тогда пара плеч AB расположена вдоль оси y, а пара с моментом B rtt (помните, что сила этой пары должна находиться в плоскости, перпендикулярной k / n, и что эта пара должна смотреть против часовой стрелки от края mx). АБ пара силдер. Без труда вычислите V V-Ab, из которого AB = ^. от / я,= = ФА, AB AB= -. Сила V и V\, приложенные в точке A, сбалансированы и могут быть отброшены. Теперь система сил сводитс

к паре сил, которые имеют силу V, приложенную в точке Vy, и силу m>, которая может передаваться и направляться параллельно силе V. линия действия силы V, приложенной в точке B, является центральной осью、 НМН. Потому что AB = A OA = a, OB = −5. Наконец, матч с 1 / = M = FA、 Обучен первому решению задачи. Имейте в виду, что метод прямого построения, который применяется во 2-м решении этой задачи, может быть успешно использован только в простейшем cases. So, при равных по модулю силах Fx и f \ 2, все углы, полученные при построении, были равны 45°.Если ис

пользовать неравные силы Ft и Flt, чтобы немного усложнить задачу, то определить расположение центральной оси будет довольно сложно. Рекомендуется использовать уравнение центральной оси (16*). Формулы (1) и (6 )для следующего:: УФЛ-2fs по-xft_ (Ай)% 0 \ » АФ ф * ф откуда Z = — = r x, y = — 77glgy * (большой, при условии этой задачи ’Я * 1. * \ | Интернет / = / / = Ф, р = / х, г=^/, т. е. центральная ось XZ находится в плоскости, параллельной координатной плоскости и отстоящей друг от друга АФТ

Тогда на расстоянии y = PT’. «это я И. В. Рекомендуется решить следующие задачи из»сборника задач теоретической механики» после издания 1950-х годов.232、234、236、237、240、241。

Смотрите также:

Предмет теоретическая механика

Графическая статистика и методы расчета ферм	Центр тяжести
Система сходящихся сил	Траектория и уравнения движения точки