Произвольная плоская система сил. Случай параллельных сил

Оглавление:

Это изображение имеет пустой атрибут alt; его имя файла - image-10-1.png

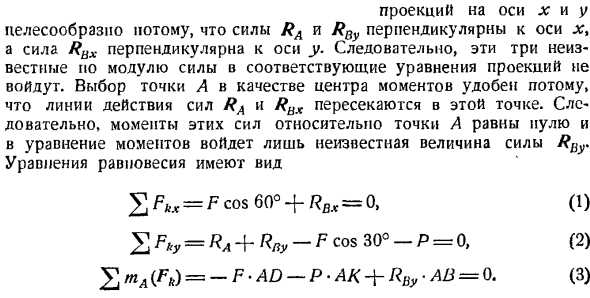
Произвольная плоская система сил. Случай параллельных сил

Любая система плоской мощности. Параллельный силовой корпус 1°.Равновесие твердых тел при наличии плоской системы сил. Напомним, что с самого начала равнодействующая сила 2 параллельных сил, направленных в одном направлении, равна сумме и величине модулей этих сил, которые направлены в одном направлении. Линия Тогда момент синтеза в любой точке будет равен сумме моментов данной силы в той же точке (теорема бариона). л. k = I г) главный вектор системы V и главный момент m0 равны нулю: Y = 0.? Р0 = 0. 1.32.

Уравнения равновесия твердых тел под действием любой плоской силы. Для равновесия твердых тел под действием любых плоских сил необходимо и достаточно, чтобы сумма проекций всех сил на произвольно выбранные оси декартовых координат x и y, а также сумма моментов этих сил для произвольно выбранных точек O, была равна нулю.：

Эта система сил приложена и находится в равновесии Людмила Фирмаль

Я… 2 = 2 Ф»,= О, 2 ″ оС » >= °- (я *） л — и к»| к = I Для плоской системы любой силы, если алгебраические неизвестные равны 3 или меньше, задача определяется статически.

Например, вы можете ограничить его, чтобы создать 1 уравнение проекции на оси x, но в то же время вы можете создать 2 уравнения момента для 2 произвольных точек. £Fkx = 0,£=°> A X») =0.(2 *） л-1 л — = Дж к-я Ось, на которой должно быть составлено уравнение проекции, не должна располагаться перпендикулярно прямой линии через точку 2, на которой должно быть составлено уравнение момента.

Если это условие не выполняется, то проекционное уравнение является результатом уравнения момента, и решение такой равновесной системы позволяет определить не 3, а только 2 неизвестные величины. Вы можете настроить уравнение 3 моментов относительно 3 произвольно выбранных точек, минуя редактирование уравнения проективной силы.

С.（/％）= 0、2 //7.d (Fk)= 0, 2 tf(Fk)= 0.(3 *） А = л А-я / Г = » я Обратите внимание, что эти 3 точки не должны находиться на 1 Прямой линии. Если вы этого не сделаете, то 1 из уравнения равновесия будут другие 2 результата. 、 2 Fbx =°> S =(4 *） к = я = я Кроме того, ось x не перпендикулярна заданной силе.

Уравнение равновесия твердого тела под действием плоской системы параллельных сил Людмила Фирмаль

Если алгебраические неизвестные равны 2, то задачи определяются статически. Вы можете создать 2 уравнения моментов для любых выбранных 2 точек без использования уравнений проекции. £тп(ФК)= 0, x ТВ С7 *)= 0-(5 *） к = \ к = \ Обратите внимание, что эти 2 точки не должны находиться на прямой, параллельной данной силе.

В противном случае одно из уравнений равновесия будет результатом другого. При решении задачи о жестком равновесии, в которой применяется плоская система параллельных сил, необходимо соблюсти первые 4 пункта, которые указаны в начале книги на стр. Дж> 5) убедитесь, что эта проблема определена статически.

То есть алгебраические неизвестные могут быть до 2. 6) Выберите ось системы декартовых координат. 7) создайте уравнения равновесия для системы параллельных сил. 8) после решения уравнения равновесия определите неизвестные величины. Если окажется, что величина неизвестной силы отрицательна, это означает, что направление этой силы противоположно тому, которое показано на диаграмме.

Рекомендуется направлять оси декартовых координат так, чтобы 1 из них была параллельна всем силам, приложенным к solid. It рекомендуется, чтобы уравнение моментов находилось относительно точки, лежащей на линии действия неизвестной силы. Это позволяет определить 1 из неизвестных величин непосредственно из уравнения момента.

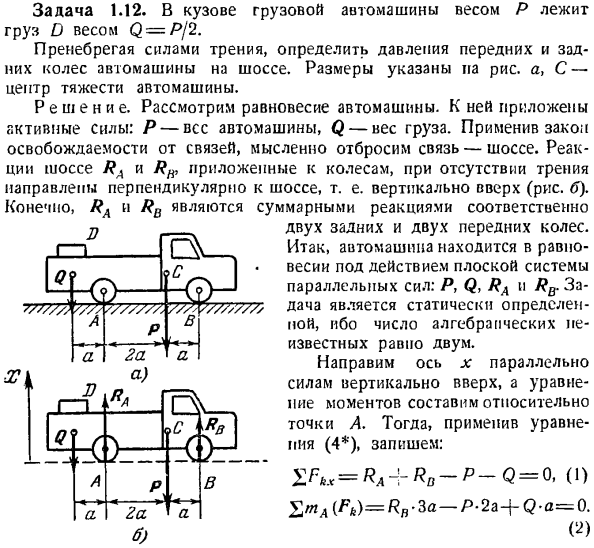
Когда вы решаете задачу, используя уравнения с двумя моментами, нет 6-й точки для решения problem. It не следует забывать, что относительная точка, в которой составляется уравнение моментов, не находится на прямой, параллельной силе. Задача 1.12. Взвешивание P за гусеницей находится груз D весом Q = Pj2. Определите давление на передние и задние колеса автомобиля на трассе, игнорируя силу трения.

Размеры показаны на рисунке. a, C-это центр тяжести автомобиля. The solution. Be обязательно учитывайте баланс автомобиля. К нему прилагалась активная сила: Р-масса автомобиля, Q-масса груза. Мысленно разрывает связь, применяя закон иммунитета-то highway. In при отсутствии трения реакция магистралей RA и RH, приложенных к колесам, направлена перпендикулярно магистрали, то есть вертикально вверх(рис. Б).

Конечно, Ra и Rd-это все реакции, соответственно. Ха. Д. ГСП. 77L 77777777 / B ？/ Вт>/ 7777777 Р 2А а） Но… Джей Джей. РА. Но… Так… 2 задних колеса и 2 передних колеса. Именно поэтому автомобиль находится в состоянии равновесия под действием плоской системы параллельных сил P, Q, RA и RB. Поскольку алгебраические неизвестные равны 2, Задача определяется статически.

К выпуску 1.12.Из Формулы (2) рассмотрим Как Q = R / 2, найти Rn = Pj2.Подставляя значение этого рН в Формуле(1), мы получим РА- = П. Так… = «Д = А(3） Давление колеса, необходимое на трассе, равно реакции, которой соответствует абсолютное значение, в противоположном направлении, то есть вертикально вниз. Эта задача может быть решена с помощью уравнения равновесия, каждое из которых содержит только 1 неизвестную величину.

По этой причине вместо уравнения (1), содержащего 2 неизвестные величины Ra и Rw, необходимо составить уравнение моментов для точки B. Это уравнение удобно тем, что RB не входит(момент силы для точки B Rn равен нулю). 2Мб (ФК)= — РА. Ла-\ — П-А + В. 4а =:0 (4） Из Формулы (4) при Q = P / 2 получаем раз = P непосредственно(см. Формулу(3)). Задача 1.13. Консольное АО Р = 4 Т находится в 2 опорах Б и О, а опора Б — в roller. At конец A, вертикальный фокус F = 8 T добавляется к лучу.

Сечение со балки имеет равномерно распределенную силовую нагрузку#= 0,5 т / м(сила-величина силы, действующей на единицу длины).в сечении АВ к балке прикладывается сила момента t = 6 ТМ. B и o поддержка для определения реакции. Размеры показаны на рисунке. Решение. Рассмотрим баланс консольной балки AD(часть балки AB вне опоры называется консолью).

Активная сила действует на балку. Вес балки I, балка I, приложенная к центру, вертикальная сила F, результирующая P {распределенная нагрузка (Px = q * CO = 1 G), приложенная к центру поперечного сечения балки, и, наконец, пара сил в момент t. Примените закон прощения облигаций к реакции поддержки Ru По вертикали upwards. In равновесное состояние пучка, главный вектор и главный момент равны нулю.

Основной вектор равен сумме вертикальных сил Fy P, Pit RB и опорной реактивной силы RD(основной вектор пары сил равен нулю). т. Да.） И Так… т. П’. 7. Эй. т. < 1 Так… 31. Д. т. 2а.• У / — ч э— \ К задаче 1.13. Момент равнодействующей силы Px. Что купить： = + =（1）= 4 + ^ .3 + ^ −1 = 0 (2） Удобство составленного уравнения состоит в том, что каждое содержит только 1 неизвестную величину.

Из уравнений(1)и(2) можно увидеть следующее: Rd = −0,75 Т; RB = 13,75 г. Отрицательное значение указывает на то, что направление силы Rn противоположно направлению, показанному на рисунке, то есть опорная реакция RD направлена вертикально вниз. Задача 1.14.Равномерная горизонтальная балка сечением D AB = = 800 Н зажата между стенками (рисунок а).

К балке приложена вертикальная концентрация/ g = 1200 н и некоторые силы, которые стремятся повернуть балку по часовой стрелке. Момент пары равен m = 600 / j, где/ — длина свободного конца балки и равен 2 м. Определите реакцию и момент реакции пары в защемленном сечении D. размеры приведены на рисунке. Длина защемленной части балки игнорируется. Решение.

Рассмотрим баланс луча. К нему прикладывается активная сила: пара сил Р, F и в момент t. слепое встраивание балки в стену препятствует перемещению балки вертикально вниз, а также вращению по часовой стрелке в вертикальной плоскости под действием активной силы.

Таким образом, необходимо компенсировать воздействие на балку парой противодействующих сил, которая пытается повернуть балку против часовой стрелки с помощью счетчика RD, применяя закон свободного от сцепления и отбрасывая стенку мысленно(рисунок Б).Основным вектором является сумма Pt F и реакции RD (помните, что основной вектор для каждой пары равен нулю).

в равновесном состоянии пучка основной вектор равен нулю, а сила P \ l F перпендикулярна, так что реакция RD также направлена перпендикулярно(рисунок B). Я… 77. B’AD C 1 Л. я-ИС −1. один.） Так… Дж. 177.、 (ЕСУ L_ з б.） К задаче 1.14. Вращая активную и реактивную пары так, чтобы силы, входящие в них, были направлены вертикально, вы получаете плоскую систему параллельных сил.

Эта задача статически определена, поскольку неизвестное число равно 2 (RD и т0).Проходить. О создании уравнений равновесия. Создайте уравнение проекции на вертикальной оси y и уравнение момента для точки D. 2Fky = РД-п-ф = о、 Из первого выражения найдено Rn = P + F = 2000 i, а из второго выражения получено/ i = 3800 j. Каковы положительные значения RD и w?

Указывает, что направление силы Rd и встречная пара моментов t были выбраны правильно. Я… В. Мещерский рекомендует решать следующие задачи «сборника задач теоретической механики» начиная с 1950-х годов: 78, 87, 89, 90. Система сил любой плоскости применяется для решения задачи о жесткости equilibrium.

To решая эти задачи, вам нужно заполнить первые 15 пунктов, которые указаны в начале книги, если в ней 15 страниц. 5) убедитесь, что указанная задача определена статически, то есть количество неизвестных величин равно 3 или меньше. 0) выберите направление оси и точку (или несколько точек) декартовой системы координат. coordinates. In напротив, вы создаете уравнение на данный момент.

женная к центру, вертикальная сила F, результирующая P {распределенная нагрузка (Px = q * CO = 1 G), приложенная к центру поперечного сечения балки, и, наконец, пара сил в момент t. Примените закон прощения облигаций к реакции поддержки Ru

По вертикали upwards. In равновесное состояние пучка, главный вектор и главный момент равны нулю. Основной вектор равен сумме вертикальных сил Fy P, Pit RB и опорной реактивной силы RD(основной вектор пары сил равен нулю). т. Да.） И Так… т. П’. 7. Эй. т. < 1 Так… 31. Д. т. 2а.• У / — ч э— \

К задаче 1.13. Момент равнодействующей силы Px. Что купить： = + =（1）= 4 + ^ .3 + ^ −1 = 0 (2） Удобство составленного уравнения состоит в том, что каждое содержит только 1 неизвестную величину. Из уравнений(1)и(2) можно увидеть следующее: Rd = −0,75 Т; RB = 13,75 г.

Отрицательное значение указывает на то, что направление силы Rn противоположно направлению, показанному на рисунке, то есть опорная реакция RD направлена вертикально вниз. Задача 1.14.Равномерная горизонтальная балка сечением D AB = = 800 Н зажата между стенками (рисунок а).

Длина защемленной части балки игнорируется. Решение. Рассмотрим баланс луча. К нему прикладывается активная сила: пара сил Р, F и в момент t. слепое встраивание балки в стену препятствует перемещению балки вертикально вниз, а также вращению по часовой стрелке в вертикальной плоскости под действием активной силы.

Каковы положительные значения RD и w? Указывает, что направление силы Rd и встречная пара моментов t были выбраны правильно. Я… В. Мещерский рекомендует решать следующие задачи «сборника задач теоретической механики» начиная с 1950-х годов: 78, 87, 89, 90. Система сил любой плоскости применяется для решения задачи о жесткости equilibrium.

7) создайте уравнения равновесия для твердых тел. 8) решить полученную систему уравнений равновесия и определить неизвестные величины. Уравнение равновесия может быть составлено в любой возможной форме(уравнение на стр. 44 выше (I*）、（2 *）、（3 *）(см.) Необходимо стремиться к приобретению такого уравнения равновесия.

Каждое уравнение содержит только 1 неизвестный quantity. In в этом случае каждая из неизвестных величин может быть определена непосредственно из соответствующего уравнения. По этой причине рекомендуется ориентировать оси координат таким образом, чтобы некоторые неизвестные силы были перпендикулярны им axes. In в этом случае величина этих неизвестных сил не входит в соответствующие проекционные уравнения.

Центр момента, то есть относительная точка, создающая уравнение момента, должна быть выбрана на пересечении 2 линий действия неизвестной силы. Это позволяет определить значение 3-й неизвестной силы непосредственно из соответствующего уравнения момента. Однако если центр этого момента устроен таким образом, что вычисление плеча становится очень затруднительным при определении момента силы, то лучше составить уравнение момента относительно другого центра, включая величину.

Дыхание неизвестной силы и результирующая система уравнений решаются вместе. Если направление реакции сцепления неизвестно, ее следует заменить на 2 составляющие и направить параллельно оси Х в направлении положительного ориентира. Если в результате решения получается, что знак величины силы отрицательный, это означает, что направление силы противоположно направлению, ранее указанному на диаграмме.

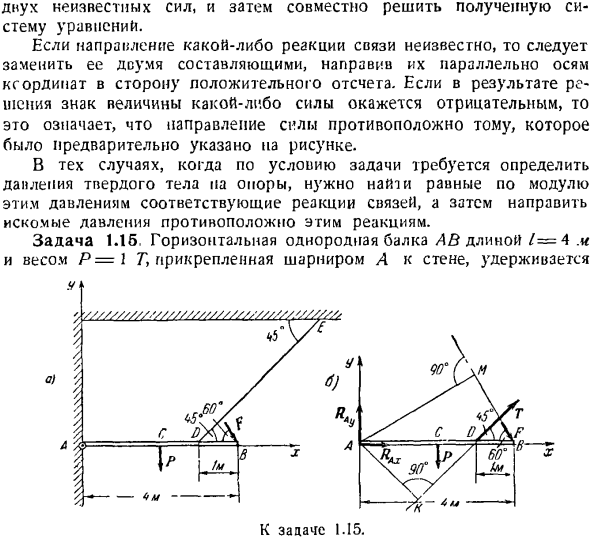
Если, в силу условий задачи, необходимо определить давление твердых тел на носитель, то необходимо найти соответствующую реакцию связывания с этими давлениями как метод, а затем направить искомое давление противоположно этим реакциям. Задача 1.15.Горизонтальная однородная Балка A B длиной f = 4 м, весом P = 1 г крепится к стене с помощью шарнира L и удерживается. один.）

К задаче 1.15. л. Так… Он находится в равновесии с кабелем DE, расположенным под углом 45°к горизонту; DB = I м. концентрация F = 2T>добавляется к свободному концу балки B, образуя горизонтальную линию и угол 60°. Определить луча давления и натяжения троса-де-совместные А. Решение. Рассмотрим баланс пучка AB, на который воздействуют 2 активные силы: вес пучка P, приложенный к середине (AC = CB = 2m), и концентрация F, приложенная к краю пучка B. Луч перекрыт с 2 связями шарнира A и кабеля DE.

Мысленно оборвите трос Дей и замените действие троса по отношению к балке реакцией троса ту, направленной из точки D в сторону обрыва. Направление реакции соединения а не может быть указано в advance. So, обозначим 2 компонента этой реакции, которые перпендикулярны друг другу. давайте переместим ось x вправо по горизонтали, а ось y вверх по вертикали вдоль оси луча.

Компоненты реакции RAx и ЯАу направлены в стороны вдоль осей координат. В настоящее время пучок можно считать свободным твердым телом, находящимся в равновесии под действием 5 сил, и только 3 силы T, RAx и размер Луча неизвестны. Поэтому задача определяется статически. построить уравнение равновесия пучка в проекции осей x и y и уравнение момента, связанного с точкой A.

It полезно выбрать точку а в качестве центра момента, поскольку момент неизвестных 2 сил при величине RAx и Луча, связанных с точкой А, равен нулю, и только 1 входит в уравнение момента 7.Форма уравнения равновесия имеет вид 2 Fkx = Rax + 7 cos 45°+ F cos 60°= 0、 £Fky-RAy-P + T cos 45° — F cos 30°= 0、 мам(ФК)= т-ак-П•АС-Ф•АМ = 0 Из Формулы(3)、 7-П П Д ^ Дж АК Ф АК ’ «Как взломать 3. К. AC = 2 Mt AK = AD sin 45°= — V2 m、 AM = AB sin 60°= 2] / 3 м, Г= + 2/3) = 4.2 Г.

Подставляя значение этой 7 в выражения(1) и (2), получаем следующее выражение: RAx =-3.96 7,RAv = −0.23 7. Знак минус выражения RAx указывает на то, что направления I и 2 компонентов реакции шарнира RAx противоположны тем, которые показаны на Рис.1. b, то есть мощность RAx горизонтально направлена влево. Аналогично, сила RAv направлена вертикально вниз.

Давление балки в искомом шарнире направлено в противоположную сторону к реакции соответствующего шарнира, и величина равна, то есть горизонтальная составляющая силы, действующей на шарнир, равна 3,96 Т, направленная горизонтально вправо, а если составляющая силы, действующей на шарнир, равна 0 23 т, то горизонтальная составляющая силы, действующей на шарнир, равна 3,96 т. Задача 1.16.Иа Фото.

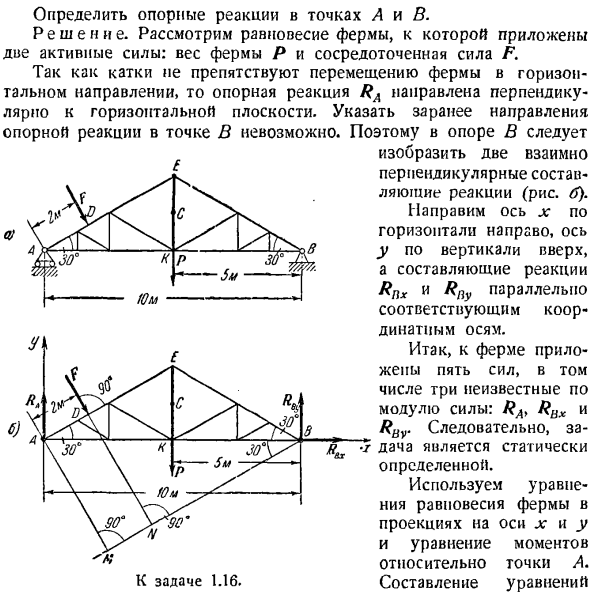
И на ней изображена симметричная стропильная ферма, которая стоит на длине f = 10 м, вес P = \ 2T, 2 опоры. Левая опора а находится на ролике, который можно перемещать вдоль горизонтальной плоскости. Расстояние/ 4£> = 2 м перпендикулярно АЭ в точке D, фокусировка F = 4 T, Z применяется пила = 30°.

Определите реакцию поддержки в точках A и B. решение. Рассмотрим равновесие фермы, где приложены 2 активные силы. Вес фермы равен P, а сила концентрации F. Ролик не препятствует горизонтальному перемещению фермы, поэтому опорная реактивная сила RA направлена перпендикулярно горизонтальной плоскости.

Направление реакции поддержки в точке B не может быть указано заранее. Таким образом, поддержка B является На ней показаны 2 взаимно перпендикулярные компоненты реакции(рис. 6). наведение оси x Около; \ ^ fC ^горизонтально вправо, ось y-вертикальное направление, Rnx и Rfly параллельны соответствующим координатным осям. Таким образом, к ферме приложены 5 сил, в том числе 3 неизвестных по модулю силы. RA> RUx и$ ^ L ^ CAJ 8 Rbv поэтому、

Коттедж определяется статически. Используйте уравнения равновесия фермы для проекции оси хны и уравнение моментов для точки А. Состав уравнения К задаче 1.16. проекция на ось l: Y рекомендуется, поскольку силы RA и R0y перпендикулярны оси l, а силы RUx перпендикулярны оси y axis. So эти 3 неизвестные степени по модулю не входят в соответствующие уравнения проекции.

Выбор точки A в качестве центра момента полезен, потому что сила RA пересекает линию действия RBX в этом point. As в результате момент этих сил для точки А равен пуле, и только неизвестное значение силы RBy%входит в уравнение момента. 2^, = Fcos60°+/?B,= 0, (1） В fky по = РА-Ф — моего-Ф в COS 30°-Р = 0,(2） ^ ма {ФК)= — Р * ад-Р■АК + RBy-АВ =0.(3） Из Формулы(3) можно увидеть следующее: Н Л * Ву АВ* * AO = 2 m, AK = 6 m, AB = 10 m, F = 4 T, P = 12 T9, мы получаем это G.

Если мы присвоим это значение RBy Формуле(2), т. из Формулы (1), RB * = = — Fcos 60°= −2 7. Знак минус, полученный уравнением RBx, указывает на то, что направление компонента опорной реакции RBx противоположно направлению, показанному на рисунке, то есть сила RBx направлена горизонтально влево.

При решении системы уравнений (1), (2) и (3) неизвестные силовые модули RBx и RBy определялись непосредственно из уравнений. (1) и(3). необходимо было вычислить только величину силы RA из уравнения. (2)назначьте ему RBy. Однако можно построить систему уравнений равновесия так, что каждое уравнение определяет каждое неизвестное независимо от другого equations.

In дело в том, что вместо уравнения (2) Держите уравнения (1) и (3), чтобы составить уравнение таких моментов так, чтобы в него входил только один Ra, как 1 шаг. Для этого необходимо, чтобы момент других 2 неизвестных сил, то есть RBx и RBV, был равен bullet. It легко выполнить это условие, выбрав пересечение линий действия этих сил в качестве центра момента, то есть точки B.

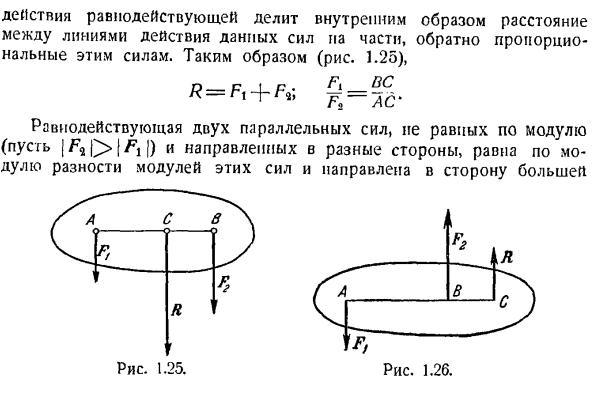
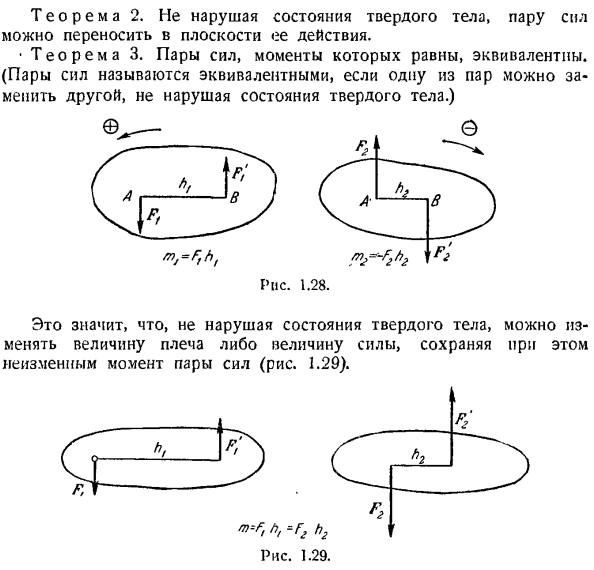
Таким образом, вместо уравнения (2) мы создадим уравнение момента силы относительно точки B. 2imB(ФК)= — РА. AB — \ — P. KB + F. NB =0.(4） Найти непосредственно из Формулы (4)： ** * AB 1 AB ’ Сила. Полученная линия действия внешне делит расстояние между линиями действия силы Она пропорциональна этим силам. Поэтому(рисунок 1.26）、 9 = з- Система из двух параллельных сил, равных по величине и направленных в разные стороны, называется парой сил(рис.1.27).Расстояние между линиями действия этих сил называется парными плечами.

Поскольку 2 силы одинаковой величины и разных направлений не находятся на одной линии действия, то 2 и 3 силы, приложенные к твердому телу, не находятся в равновесии. Пара сил будет пытаться вращать твердое тело, к которому она приложена. Мерой действия пары сил является алгебраическая величина, называемая моментом. Абсолютное значение момента пары сил равно произведению пары силовых модулей на плечо.

Если пара сил выглядит против часовой стрелки, то момент пары положителен, а если по часовой стрелке, negative. An пример показан на рисунке. 1.28. Теория пар сил на плоскости сводится к 4 теоремам. Теорема 1.Алгебраическая сумма моментов сил, составляющих пару относительно любой точки на плоскости, не зависит от выбора этой точки, А равна паре моментов.

Рис. 1.27. КВ = Б М, АВ = 10 журналов, в£= Аф£ — соѕ 30°- _ Ад = 5-2-6. 65 м, р-12 7, F = 4 г, RA = 8,66 т. Задача 1.17.Поняв состояние и решение задачи 1.0, определим силу u^, учитывающую вес суппорта, которая приложена в центре тяжести C и равна P = 60 кг. The solution. In задача 1.6 мы использовали теорему о 3 непараллельных силах для исследования равновесия суппорта при действии 3 сил N, F, RA. К этим силам прилагается вес опоры R.

Благодаря этому, возможности отнимаются! Затем мы применяем теорему о 3 непараллельных силах, которая может определить положение линии реакции RA цилиндрического соединения A. На рисунке показана ось x, указывающая горизонтально вправо, и ось y, указывающая вертикально вверх. О компонентах RAx и RAy. Итак, опора находится в равновесии под действием флета

К задаче 1.17. = 46-1 = 23 см (используется здесь Уравнение вещества 1.6(1).Если мы присвоим эти значения (4), мы узнаем. IAU = SHKG. (5） Тогда из Формул(1) и(2), RAx = NCO 60°= 300 — ^ — = 150 кг、 F = P — \ — N cos 30° — RAy = 60+ 1501/3-260 60 кг. RAx = 150 кг, F = 60 кгг.(6） Используя результаты (5) и (6), рассчитайте коэффициент реактивной силы RA цилиндрического соединения A по формуле. РА = ВР * ах + Р \ в Что купить： Ra = 300kH(7）

Как и ожидалось, включение опорной силы тяжести P в суппорт оказало влияние на увеличение силы реакции RA и силы упругости F. решение zappy1. 6 без учета опорного веса эти силы стали равны модулю упругости:?D = 275 кг, F = 30 кг (см. уравнение (3) выпуска 1.6). Как и в предыдущей задаче, вместо уравнения (2) можно создать уравнение момента относительно точки А.

Таким образом, сила F- Конечно, задача 1.6 — это система уравнений（1）、（2）、（3）вы также можете решить эту проблему с помощью следующей команды на самом деле, если вы получаете P = 0 в этих уравнениях, это выглядит так: RAx= \ 50 k T, RAy = 230 k1 \ F-30 kG、 Таким образом, РА = Р / \ х-р ^ ХV-^• Я… V. рекомендуется решить следующие задачи из»сборника задач теоретической механики» после 1050 г. Мещерского：122、123、129、133、134、135、136、140。

2°.Твердый обломок автобуса. При изучении остального твердого тела (структуры) возникает проблема, что необходимо определить пределы силы или размера, обеспечивающие поддержание этого condition. In при этих проблемах тело наклоняется примерно на 1 пункт, как правило, с усилием, превышающим максимально допустимое значение, которое обеспечивает оставшийся твердый гель.

Такая задача решается в предположении, что твердое тело начинает отклоняться от 1 столба. Поэтому реакцию этой поддержки рассматривать не стоит. Затем, при твердом равновесии, реакция остальных опор должна быть уравновешена результатом действия всех активных сил. Это означает, что линия действия равнодействующей силы всех активных сил проходит через оставшуюся опору, поэтому момент равнодействующей силы против точки опоры равен нулю.

Таким образом, сумма моментов по теореме валина Ноль для всех активных сил, связанных с точкой опоры 0： н. 2 «о’ C7*)= L = 1 Из этого уравнения определяется предельное значение силы или размера твердого тела, при котором падение еще не происходит. Решение задачи твердой инкапсуляции должно осуществляться в следующем порядке: 1) изобразить активную силу; 2) Определите опоры, которые могут опрокинуться. 3) Создайте уравнение для момента действительной силы, связанной с этой точкой опоры.

4) после решения уравнения определите желаемое значение (конечную силу или конечный размер). Задача 1.18. Горизонтальный кантилевер переменного тока весом Р расположен на опорах а и В, а опора а находится на роликах, которые не мешают движению вверх movement. To консольный конец C Сосредоточенная вертикальная сила F приложена к балке C, которая определяет максимальное значение силы F, при котором балка остается неподвижной.

Размеры, показанные на рисунке, составляют 2м. К задаче 1.18.Решение. О действии луча 2 активные силы: центр балки, то есть вес балки Р прибавляется к расстоянию 1 м от опоры в, F-конец консоли, то есть концентрация, приложенная к точке С. Если величина силы F велика, то видно, что балка наклоняется по часовой стрелке вокруг опоры B. Чтобы определить максимальное значение силы F, сумма моментов активной силы в точке

B должна быть равна нулю.%mB (Fk)= p. l-F-2 = 0、 Р П Если есть шар, от которого F =сила перекатывается ki поворачивает опору B по часовой стрелке. — Задача 1.19.На грузовике установлен кран. Вес противовеса B равен P » = 2 т. Противовес, равный Р= 5 7 ′, применяется к пункту С. Определить минимальное расстояние DB между осями колес транспортного средства и максимальную массу P3 груза L, являющегося lifted.

In в этом случае транспортное средство не будет переворачиваться с грузом или без груза A. размеры указаны на рисунке. Решение. Активная сила приложена к тележке, на которой установлен кран: I, — масса тележки с краном без противовеса B, — масса собаки с противовесом B. Если имеется груз A, то устанавливается и его вес P3. • Использование подвешенного груза A может привести к тому, что транспортное средство будет вращаться против часовой стрелки вокруг точки D К задаче 1.19. ^ ЖВ. Vx ^ WNVVVVVVVV Я что ли Земля и передние колеса.

Если нет груза а, то транспортное средство, благодаря действию противовеса в, может упасть по часовой стрелке вокруг точки е контакта между задними колесами и ground. Do не думайте, что другие варианты подрывной деятельности практически неинтересны.

Для определения максимального значения веса поднимаемого груза A Ra и минимального расстояния DE между осями колес и обеспечения равновесия транспортного средства необходимо составить уравнение момента активной силы для точки D с учетом 1) веса P.{, 2) уравнения момента относительной активной силы

1) Выберите ось декартовых координат. 2) Выберите центр, который выведет систему сил. 3) вычислить проекцию главного вектора системы сил по формуле Vx = 2 Fkx,£Fb;、 k = \ k = I 4) определить Косинус направления с модулем основного вектора V = Vox-r Y’y потому что(Джу=£, соѕ(/ В)= — Г; 5)по формуле рассчитайте основные моменты системы сил для вырожденных центров л. m0 = 2 m0 (Fk)>где 0-центр редукции в системе сил.

О) в зависимости от значений V и m0 может быть 4 случая. Для а) VΦ0 и m0 0 0 система сводится к синтетическому Ry, равному силе V, расстояние h-m0!Он разделен V и расположен так, что знак результирующего момента относительно центра O совпадает со знаком основного момента m0 Б)если V = 0, m0 = 0, то система сил уменьшается до результата, соответствующего V. в)Если V = 0, m0 0 0, то силовая система сводится к паре сил с моментами m0\ г) Если V = 0,то −0, то система сил находится в равновесии.

Случай а) и Б) уравнение линии действия результата И он имеет форму. н. xRy-yRx = 2 m0(Fh）、 до = = Я Где Rx-Vx, Rv = Vyt и l * N y-текущие координаты точек линии влияния результата, а O-начало координат. Необходимо направить ось декартовых координат так, чтобы максимальное число возможных сил было параллельно или перпендикулярно этим осям.

Уменьшенный центр системы должен быть выбран таким образом, чтобы момент силы вокруг этого центра был как можно меньше, то есть линия действия этих сил проходит через уменьшенный центр системы. Теорема 2.Пара сил может передаваться на рабочую поверхность без нарушения твердого состояния. * Теорема 3.Пару раз равная сила эквивалентна.

(Объединение сил называется эквивалентным, если одну из пар можно заменить другой, не нарушая состояния твердого тела.)） При этом изменяется размер плеча или величина силы, не нарушая состояния твердого тела、 Заметим, что при переходе от одного редукционного центра (О) к другому главный вектор V не зависит от выбора редукционного центра (главный вектор является статическим инвариантом),

А главный момент системы изменяется по формуле. тат = М0 + ма потока(v0). Задача 1.20.Любая планарная система сил была доведена до центра O. As в результате редукции получаются сила V (см. рисунок) и 1 пара сил, момент которых равен основному моменту m0 = AVa. Определите основную точку системы этой силы при переходе к новому убывающему центру а, расположенному в старом центре вдоль расстояния Оа = а или оси Х. Решение.

Выберите ось декартовых координат, как показано на рисунке. Эту проблему можно решить двумя способами. 1.Переместите силу A в точку A. To для этого приложите 2 уравновешивающие силы V и V ’к точке A так, чтобы 1 из них был равен вектору V. пара), сюда входит сила, приложенная в точке O, сила V \ Применяется в точке А. момент сцепления mn? mnp = равно-Va. Итак, помимо силы V, приложенной к точке A,

существует сила момента m0 и mpr из 2 пар. Эти 2 пары сил эквивалентны паре сил, приводящих к моменту mA > равному mA = m0 — > mn = 4Va-Va = 3Va. Сумма та является искомой главной точкой системы сил относительно нового центра сокращения А. Таким образом, основные моменты системы изменились в результате перехода от старого центра перемещения о к новому центру А.

2.Эту задачу можно решить, используя тот факт, что сила V, равная основному вектору системы сил, является статическим инвариантом. То есть это зависит не от выбора центра торможения, а от главного момента системы changes. As вы знаете, что главным моментом плоской системы любой силы относительно нового центра торможения является алгебраическая сумма главных моментов этой системы относительно старого центра.、

О. ■ пиар И затем Что это было? Моффин. Да. 1. К выпуску 1.20. Относительно нового центра основной вектор системы прикладывается к старому центру, т. е. mA = = m0 — > m(V0).по предположению предположим, что π0= 4 Va, mA (V0)= — Va, тогда mA = 3 Va. Задача 1.21. 4 силы прилагаются к диску: F1 = F2 = /：、 FZ = FVZ, Fk = FV6 \ Приведем простейшую форму этой системы сил. Решение. O когда у вас есть начало координат xiordiat в центре диска, укажите ось x горизонтально вправо и ось y вертикально Вверх

. Определите главный вектор V и главный момент m0 системы этой силы, причем точка O является центром редукции системы. С тех пор (Да В = ВВС + кДж, М0 =£М0(ФК)Т Далее предварительно вычисляем проекции Vx и Vy главного вектора V. н. Декартовы координаты и сумма всех силовых моментов^ m0 (Fk） к ^ 1 К задаче 1.21. От точки о ЧХ = VFkx = — FJ и соѕ 30° — Фи Косинус 30°+ Ф4 потому что 45°, (2） Вы = в fky по = — ф соѕ 60°+ Ф. 2 в COS 60°-Ф3 + Ф4, потому что 45°, (3） ^ m0 (Fk)= Fi’a-F4 * a sin 45%(4）

э Где буква А обозначает радиус диска. Из (2) — (4) получаем V * = 0f Vy = 0, V m0( FJ;) = Q. выражение (1) принимает вид\ / = 0, m0 = 0. Поэтому основные векторы V и r

Решение. Выбрав начало координат декартовой системы координат в вершине треугольника A, ориентируйте ось x вправо по горизонтали, а ось y-вверх по вертикали. Определяет главный вектор и главный момент заданной плоской силы. Выберите пункт A.

Модуль основного вектора этих сил рассчитывается по формуле В = ВР \ / Ч-К? А здесь ЧХ = в fhx по = ф, — потому что GO0-Fзcos G0 и°= 0、 Vy = £Fby = F \ cos 30°-F3 cos 30°= 0 Таким образом, основной вектор равен пуле и V = 0. Основная точка этой системы сил вычисляется относительно приведенного центра А. НС(Ф) = ма(Ф3)= 0, ма(ф)= ф. рад = ^ га、

Приобретение：、- ™а = та(Центр)+ та(п)+ тп(ФЗ)= в Англии. Итак, выбрав точку а в качестве центра редукции этой системы сил, мы нашли: В = 0, та = То есть они установили, что система сил сводится к паре сил момента m = Fa. As вы знаете, при спаривании системы сил Убедитесь, что основная точка не зависит от выбора уменьшенного Центра.

Эту проблему можно решить по-другому way. So например, после передачи силы в точку A вдоль ее линии действия можно добавить силы Fl и F’V, которые будут применены в точке A (рисунок B).Сумма этих сил равна диагоналям ромба силы F1^, а угол вершины равен 120°.в этом случае диагонали ромба находятся на своих сторонах, то есть| FM / =F. So получается, что эта система сил сводится к единице силы.

Это имеет силу и плечо составляет 1/3 1’h = AD=, а момент этой пары сил равен m-Fh-Ha. 2-е решение проблемы оказалось короче. Однако следует иметь в виду, что в первом варианте необходимо принять простейшую форму любой плоской энергосистемы и постоянно использовать ее для решения более сложных задач, используя более популярные методы.

Задача 1.23.На рисунке 1 показана мощность системы Fx, F. 2, для того, чтобы fa простейшей формы. Силы Ft и F9 направлены в противоположную сторону, а сила находится на диагонали прямоугольника ADCD с A на стороне объявления. / Флорида / = = / Fq / = » 1 F3 j =F. E. выберите начало координат декартовой системы координат в вершинах прямоугольника A, а затем укажите ось x горизонтально вправо и ось y вертикально вверх.

(Выбор такого направления оси хны удобен из-за того, что 2 из 3 сил параллельны оси y и не дают проекции на ось X.） Она приводит эту систему сил в главный вектор и главный момент. Выберите начало координат системы координат в качестве центра уменьшения системы сил. ЧХ = 2Fkx = — ФА в COS 30°= — ФЛ / 3″, Вы = 2 Пкй = валютном −4—Ф и cos G0 и°=Ф. основные вектора V модулей В=] АВФ В± $ = 2 Ф9(1）

Направляющий Косинус выглядит так: потому что (*>)=£= — С -, потому что ОЦВ)= = То есть, (l:, V)= 150°, (y, V)= 60°.Сила V показана на рисунке. один. Переходя к определению главного момента системы сил против вырожденного центра А. / Тл(Ф)= тп(Ф3)= 0,и та(Ф») = Ф2-ад = ФА、 Мы это выясним： та = та(Ф)+ / Н(ФДЖ + ( / > .) = ФА.(2）

Таким образом, система сил делится на силу V и、 Известно, что в случае VF 0 и TAF 0 система сил может быть сведена к Объединенным силам R. To для этого мы изобразим пару сил, соответствующих основному моменту tA, так что величина сил, составляющих пару сил, равна силе V, а 1 из них (V)находится на той же линии действия, что и сила V и направлена в противоположную сторону direction.

этом случае 2-я сила, входящая в состав пары сил, приложенных в точке K, становится вектором, равным силе V. момент этой пары сил является главным моментом hnA> i. e. so, чтобы быть равным tA = Vh, нужно выбрать пару h = AK, откуда h = — AK = ntA / V с помощью формулы (I) и (2) Найти h-ajl. Теперь у нас есть система из 3 сил. Модуль каждой из этих сил равен модулю главного вектора V. равные по величине, направленные в противоположные стороны вдоль общей линии действия, 2 силы, приложенные к точке А, уравновешиваются.

Эти силы могут быть разрушены без нарушения твердого состояния.1 Сила V, приложенная к точке K, остается. Система питания. Таким образом, эта сила равна основному вектору V, который является синтетическим R. таким образом, удалось привести эту систему сил в синтетическое R. Результат/?Определите уравнение для линии действия. н. xRy-yRx = X t

Проекция на ось декартовых координат результирующего R равна проекции основного вектора V на соответствующую ось, т. е. Rx = =- FYs, Ry = F. сумма моментов всех этих сил относительно начала координат A является главным моментом tA, который определяется формулой(2). Зма(ФК) = ма = ФА Замена Найти уравнение линии действия R, уравнение R (3),

Значение Rxf Rvt£тА (FK), результат. / ЛТ| с Это уравнение прямой линии с угловым коэффициентом, равным −1 ^ 3/3.Это означает, что угол, образованный этой прямой линией и осью x, равен 150°. Найдите пересечение результирующих линий действия С топорами. для η= 0 y = a, для y^ ^ 0 x = a Таким образом, результат будет направлен вдоль диагонали DB прямоугольника ABCD. Добавление теоремы 4 (

Доведите силу до заданной точки. Когда сила приложена к определенной точке, добавляется пара дополнительных сил. Момент силы равен моменту определенной силы относительно центра торможения. МЖ * Ф, ХН МФ-F2h2,mfF3h3 исчерпывающим+ М2 + М3-Ф, кв-Ф2 hfFh Рис. 1.30.

Это означает, что можно добавить силу F к точке B (рис.1.31), добавив дополнительную пару моментов, равных моменту данной силы F, к уменьшающемуся центру B, не нарушая твердое состояние. При преобразовании любой плоской силовой системы в простейшую форму широко используется перемещение силы в заданную точку.

Вектор гласных V-это векторная сумма сил, приложенных к твердому телу. в£= k = I Проекции главных векторов VX и VV на оси декартовых координат равны сумме проекций этих сил на соответствующие оси. к-мне ^ = Fkx в УУ =£rky. k = I Модули основного вектора в = Вви + в $. Косинусы направления основного вектора определяются уравнением.

потому что(xGU)= Т? потому что (yPv)=. Основным моментом для центра O (tnQ), в этой связи, является сумма моментов силы, приложенной к твердому телу. Центр, а именно н. > 00 = » о°））- По определению, главный вектор v является статическим инвариантом.

То есть величина и направление основного вектора не зависят от выбора центра сжатия системы. Основные моменты системы при смене центра, вообще говоря, меняются. Главный момент tA плоской системы сил к новому центру торможения A равен сумме главного момента этой системы сил к старому центру O и главного вектора, приложенного к старому центру O Vy. ма = М0 + ма(У0). 1.

приведение к одному центру силы произвольно расположенному на плоскости. Если привести произвольно расположенную на плоскости силу к 1 центру О, то система сил преобразуется в силу, приложенную к этому центру (равную основному вектору V) и силу, момент которой равен паре главных моментов m0.

Результатом V является 1 сила, равная системе данной силы, и сила V не должна быть указана в результате, потому что она равна системе данной силы только в том случае, если момент объединен с парой сил, равных основному моменту m0. А) главный вектор равен нулю, но главный момент не равен нулю, то есть V = 0, mQ 0.0.In в этом случае основная точка системы сил не зависит от выбора центра редукции).

б)главный вектор не равен нулю, но главный момент равен нулю, т. е. k ^ 0,/∞= 0.Система сил сводится к синтетическому R-V, который прикладывается в центре сжимающейся системы. в)главный вектор системы и главный момент не равны пуле, то есть V ^ 0, т00.Система сил сводится к результату R = Vt, линия действия которого отделена от линии действия силы V на расстоянии h = rn0 / V.

положение линии действия результата R должно быть таким, чтобы знак момента результата R относительно приведенного Центра O совпадал со знаком основного момента системы сил m0 относительно центра O. Сила V и результирующая R равны по величине и параллельны(рис. 1.32). Теорема вариона для произвольной плоской системы сил. Если система сил уменьшается к результату、

Смотрите также:

Предмет теоретическая механика

Основные законы статики	Равновесие системы твердых тел
Система сходящихся сил	Равновесие тел при наличии трения