Оглавление:
Производные высших порядков явно заданной функции
Производная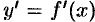 
функции 
есть также функция от 
и называется производной первого порядка.
Если функция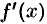 
дифференцируема, то ее производная называется производной второго порядка и обозначается 
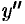(или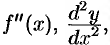 
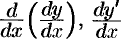) . Итак, 
.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается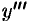 
( или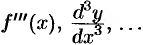 
), Итак, 
.
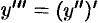Производной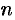 
-го порядка (или 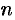-й производной) называется производная от производной (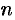-1) порядка:
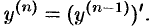
Производные порядка выше первого называются производными высших порядков.
Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (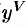
или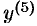 
— производная пятого порядка).
Пример №23.1.
Найти производную 13-го порядка функции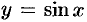 
.
Решение:
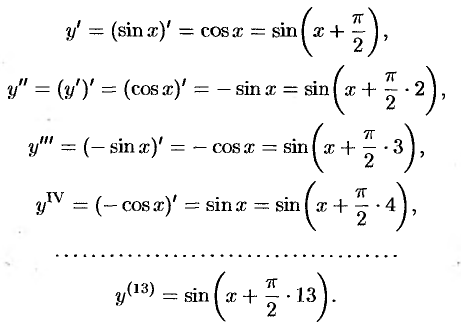
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Дифференцирование функции, заданной параметрически |
| Логарифмическое дифференцирование функций |
| Механический смысл производной второго порядка |
| Производные высших порядков неявно заданной функции |
