Оглавление:
Производные высших порядков от функций, заданных параметрически
Пусть функция 
задана параметрическими уравнениями
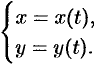
Как известно, первая производная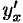 
находится по формуле
Найдем вторую производную от функции заданной параметрически.
Из определения второй производной и равенства (23.1) следует, что
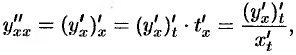
т. е.
Аналогично получаем
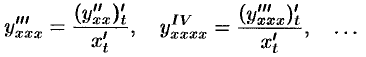
Пример №23.3.
Найти вторую производную функции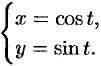 
Решение:
По формуле (23.1)
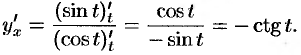
Тогда по формуле (23.2)
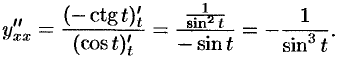
Заметим, что найти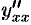 
можно по преобразованной формуле (23.2):
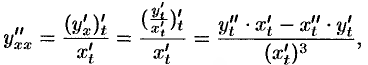
запоминать которую вряд ли стоит.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Механический смысл производной второго порядка |
| Производные высших порядков неявно заданной функции |
| Применение дифференциала к приближенным вычислениям |
| Дифференциалы высших порядков |
