Оглавление:
Производные основных элементарных функций
Степенная функция 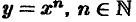
Дадим аргументу  приращение
приращение 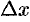 . Функция
. Функция  получит приращение
получит приращение  . По формуле бинома Ньютона имеем
. По формуле бинома Ньютона имеем

Тогда
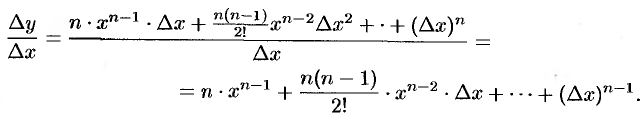
Находим предел составленного отношения при 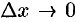 :
:
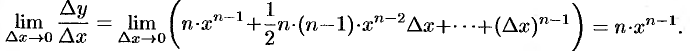
Таким образом,
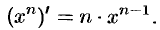
Например,  .
.
Ниже (см. замечание на с. 175) будет показано, что формула производной степенной функции справедлива при любом  (а не только натуральном).
(а не только натуральном).
Показательная функция 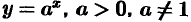
Найдем сначала производную функции  . Придав аргументу
. Придав аргументу
 приращение
приращение 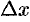 находим приращение функции
находим приращение функции 
 . Стало быть,
. Стало быть,  и
и
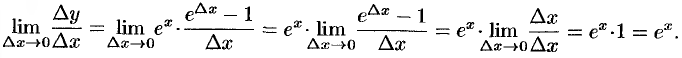
При вычислении предела воспользовались эквивалентностью  при
при  .
.
Итак,  , т. е.
, т. е.
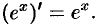
Теперь рассмотрим функцию  . Так как
. Так как  , то по формуле производной сложной функции находим:
, то по формуле производной сложной функции находим:
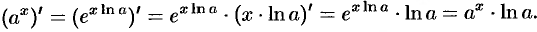
Таким образом,  .
.
Пример №20.5.
Найти производную функции  .
.
Решение:
Используя формулу производной сложной функции и формул}’ производной показательной функции, находим
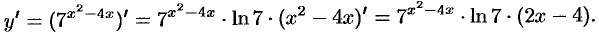
Логарифмическая функция 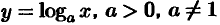
Найдем сначала производную функции  .
.
Для нее
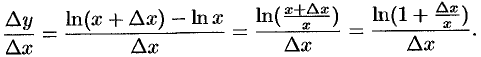
Переходя к пределу при 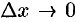 и воспользовавшись эквивалентностью
и воспользовавшись эквивалентностью  при
при 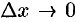 , получаем:
, получаем:
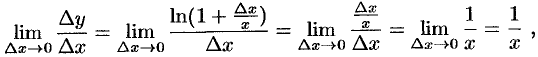
т. е.  или
или  .
.
Теперь рассмотрим функцию  .
.
Так как  , то
, то
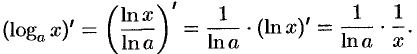
Таким образом,  .
.
Пример №20.6.
Найти производную функции  .
.
Решение:

Производную логарифмической функции  можно найти иначе. Так как обратной для нее функцией является
можно найти иначе. Так как обратной для нее функцией является  , то по формуле производной обратной функции имеем:
, то по формуле производной обратной функции имеем:
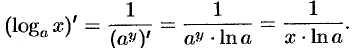
Тригонометрические функции 
Для функции 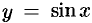 имеем:
имеем:
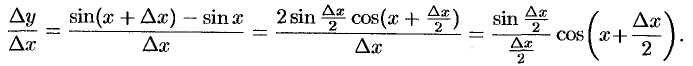
Переходя к пределу при 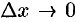 и воспользовавшись первым замечательным пределом
и воспользовавшись первым замечательным пределом  , получаем
, получаем
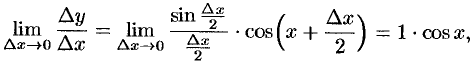
т. е. 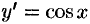 или
или  .
.
Найдем производную функции 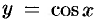 , воспользовавшись формулой производной сложной функции:
, воспользовавшись формулой производной сложной функции:
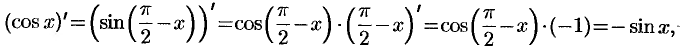
т.е.  .
.
Для нахождения производных функций  и
и  воспользуемся формулой производной частного:
воспользуемся формулой производной частного:
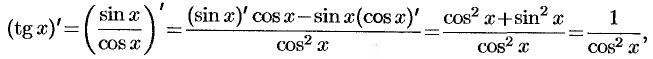
т. e.  .
.
Проделав аналогичные операции, получим формулу
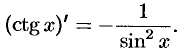
Этот результат можно получить иначе:
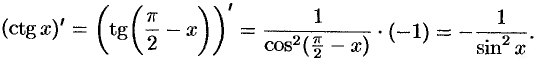
Пример №20.7.
Найти производную функции  .
.
Решение:
 .
.
Обратные тригонометрические функции 
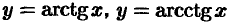
Пусть  . Обратная ей функция имеет вид
. Обратная ей функция имеет вид  ,
,  . На интервале
. На интервале  верно равенство
верно равенство  .
.
По правилу дифференцирования обратных функций
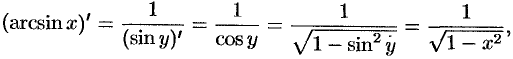
где перед корнем взят знак плюс, так как  при
при  . Итак,
. Итак,  .
.
Аналогично получаем, что  . Эту формулу можно получить проще: так как
. Эту формулу можно получить проще: так как  , т. е.
, т. е. 
 , то
, то  .
.
Найдем производную функции  .
.
Она является обратной к функции  , где
, где  .
.
Поэтому, по правилу дифференцирования обратных функций, получаем, что
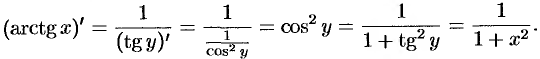
Итак,  .
.
Функции  и
и  связаны отношением
связаны отношением
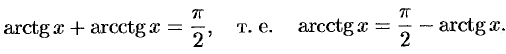
Дифференцируя это равенство, находим
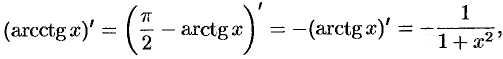
т. е.  .
.
Пример №20.8.
Найти производные функций: 


Решение:

Замечание: Найдем производную степенной функции  с любым показателем
с любым показателем  . В этом случае функция рассматривается для
. В этом случае функция рассматривается для  .
.
Можно записать  . По правилу дифференцирования сложной функции находим
. По правилу дифференцирования сложной функции находим
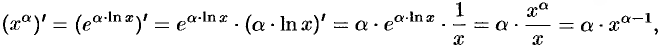
т. е.  .
.
Формула остается справедливой и для  , если функция
, если функция  существует:
существует:
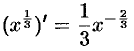
при всех 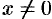 .
.
Дополнительный пример №20.9.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:

