Частными производными второго порядка функции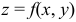 
называют частные производные от ее частных производных первого порядка. Обозначения:
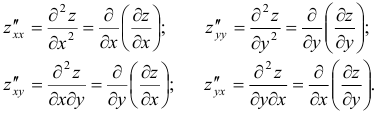
Если смешанные производные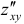 
и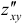 
непрерывны, то результаты дифференцирования не зависят от порядка дифференцирования, т. е. 
.
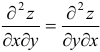Аналогично определяются частные производные более высокого порядка:
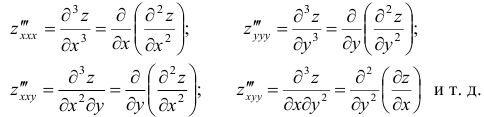
Частные производные третьего и высших порядков, отличающиеся только последовательностью дифференцирования, равны между собой при условии их непрерывности.
Дифференциалы второго, третьего и более высоких порядков функции 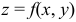определяются формулами 
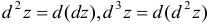и т. д. Они выражаются через частные производные следующим образом:
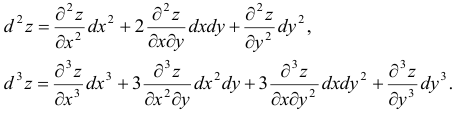
Вообще справедлива символическая формула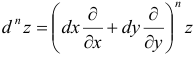 
,
которая формально раскрывается по биномиальному закону.
Пример:
Найти смешанную производную второго порядков для функции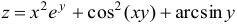 
.
Решение:
Найдем частную производную первого порядка по переменной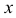 
:
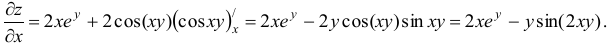
Теперь дифференцируем повторно по переменной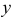 
:
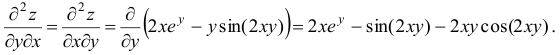
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Функций многих переменных |
| Частные производные и полный дифференциал функции |
| Касательная плоскость и нормаль к поверхности |
| Экстремум функции нескольких переменных |
