Оглавление:



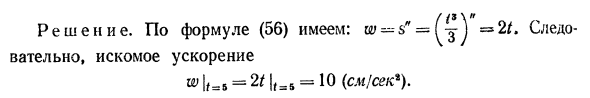
Производные высших порядков
- Высшие производные /. Найти производные высокого порядка Предположим, что функция y = f (x) дифференцируема. Его производная f ′ (x) является функцией от x. Эта функция также имеет производную. Эта производная называется второй производной или второй производной функции y = f (x) и обозначается символом y «или Γ (x). * P ) = [/ ‘()]’. (51) Кроме того, f ‘(x) называется первой или первой производной функции f (x). Пример 1. Найти вторую производную функции y = x *.
Решения. Найдите первую производную этой функции. у ‘= (х *)’ = 3х2. . Производная второй производной функции y-f (x) называется третьей или третьей производной этой функции и представлена символом y «‘или /»‘ (x). / «‘() = [T ()]’. (52) В общем, n-я производная функции y = f (x) является первой производной (n-1) -ой производной данной функции, выраженной как y (n) или fin) (x) вы. / <«‘(*) == [G-1 * ()]’ • (53) Производная порядка выше первого порядка называется производной высшего порядка.
Найти вторую производную как производную от первой производной Людмила Фирмаль
Пример 2. Найти четвертую производную функции y- \ nx. Решения. Найти производные первого, второго, третьего и четвертого порядка подряд. ✓ = () ‘»!!;,'» = (- ^ ‘= 1, „G (2V 6 Пример 3. Найти n-ю производную функции y = exx. Решения. У нас есть: y ‘= (e **)’ = kekx \ y «= (& **) ‘= k2ekx \ y'» = <Нет. *) ‘ По аналогии Инь) = Кенккс. (54) Пример 4. Найти n-ю производную функции y = smx.Решения. У нас есть: y ‘= (sin x)’ = cos x = sin [x -f- ~ ^; Y = (cosx) ‘= -inx = sin (x + ^ -2 ^; = -sin x) ‘= -coSA: = sin +); f / v = (-cos ) ‘= sinlg = sin • По аналогии ^> = sin ( + f./i)*. (55) 2. Механический смысл второй производной В § 4 § 1 выяснилось механическое значение первой производной.
Давайте рассмотрим механический смысл второй производной. Заставить материальную точку двигаться линейно по закону s = / (/). Где s — маршрут, пройденный по времени t. И скорость этого движения также является функцией времени: v = v (t). В момент времени t значение скорости равно v = v (t). Рассмотрим еще один момент времени t-> At. Ей соответствует значение скорости vx = v (t + At). Приращение времени At соответствует приращению скорости Отношение Av = vi-v = v (t-j-At) -v (t) = ^ называется средним ускорением за интервал времени At.
| Непрерывные функции | Дифференциал функции |
| Производная | Функции, заданные параметрически, и их дифференцирование |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Ускорение w в момент времени t является пределом среднего ускорения при A / — »- 0. w = lim wco = lim ^ = vt. Таким образом, ускорение тонкого линейного движения является производной скорости по времени. Как мы уже видели, скорость является производной пути s по времени s: v = s ‘. Учитывая это, есть следующее: w ^ v’t ^ (s’Y = s \ (56) Следовательно, ускорение линейного движения немного равно второй производной по времени.
Пример * Заставить точку массы двигаться линейно Происходит в соответствии с законом s = 3- Где время t выражается в секундах и пути s —Ссылка. Найти ускорение w движущейся точки в момент времени t-5 секунд.Решения.
Уравнение (56) дает: -s «= (^» s * JNext- Желаемое ускорение =% | G = 5 = 10 (см / с *). Людмила Фирмаль

