Оглавление:


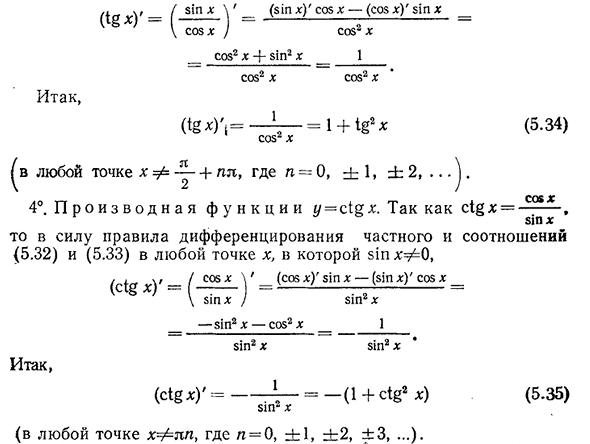

Производные тригонометрических функций
- Производная тригонометрической функции. 1°. П р О и ЗВ о д н а я ф у Н К Ц и я у=51ph.Для этой функции Du=81TS(h+DH) — 81PH=2so8^h+81D-u -, то для любого DH#=0 отношение разности равно、: DH. 81P ——-
Два. По определению производных DH. 81P — — (81p’х)’=соз(Х4—- — ———- ДХ- «о, ДХ ДХ-» о\2/ДХ (5.29)) Непрерывность функции#=
Cox гарантирует, что любая точка x бесконечной прямой Поп-игла(х+ = Людмила Фирмаль
поп х(5.30) DH — » o\2 / 206 Глава 5. Дифференциальное исчисление Кроме того, благодаря первым заметным ограничениям и базовому DH * ** См. пункт 1, 3 Формулы (5.13). * См.§4, третью формулу(5.24).
Изменение переменных DH. Н т———— = и t — ^2 — =1. (5.31) DH-M) DH< — > 0 / Два. Из существования предела(5.30) и(5.31)и из теоремы о пределе произведения двух функций следует существование предела правой части(5.29)и равенство (WSH x)’=N t DH-I) Поп Х О!.
81P ——— Два. DH2 — SO5X Так… , (8 1P H) / =SO8H(5.32) (Для любой точки x бесконечной прямой). 2°. П р О я з В О Д н а я ф у Н К И Й=coz X. Тогда по правилам и уравнению дифференцирования
комплексных функций(5.32)) =Соз- — — — ч^(-1)= — 81PH. Так… , (soah)’= — 81P x (5.33) (для любой точки x в бесконечной прямой). 3°. П р О я з В О Д н а я ф у Н К и г/=1дн. 1§x=81x или более поздняя версия, pop X То есть по правилам производных от частного * **и соотношений (5.32) и (5.33) в любой точке x поп x=H=0, * Очевидно,§5. Производная от элементарной элементарной функции 207 31Р х’(31Р%) поп-х —
(поп х)’ 51p позволяют вести съемку быстро х Поп х) CO2X P2X+81P2X _ 1 COZ2X COZ2X Так… , Два. г -=1+1§2х(5-34) X2X Любая точка x= / = — ^ — +PL Людмила Фирмаль
, где n=0,±1. ±2,… 4°. П р О И З В О Д н а я ж у Н К И Й=s1gh. От 81P X Тогда по правилу производной в любой точке x частного и соотношений (5.32) и (5.33) 5sh x+=0, Поп х V__(поп Х) ‘ — 31П Х—(81P х) поп ХХ 81P/31P2X — 81P2X-SO32X 31P2X Один._ 8X2X Так… , (С!§х)’ ——— = — (! +c1e2 *) $ 11Г Х (5.35 утра)) (В любой точке x=^LP, где n= 0, ±1, ±2, ±3, …да что с тобой такое
Смотрите также:
Методическое пособие по математическому анализу
| Общая схема отыскания экстремумов | Обратные тригонометрические функции |
| Тригонометрические функции | Гиперболические функции |

