Производные функции нескольких переменных

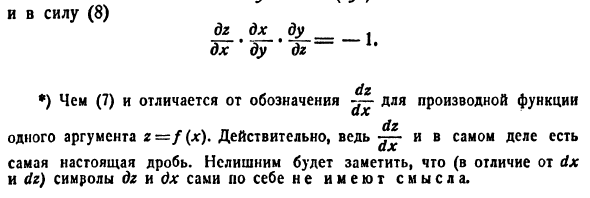
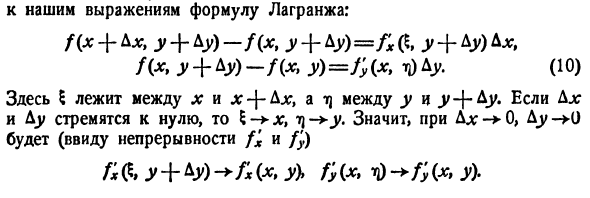
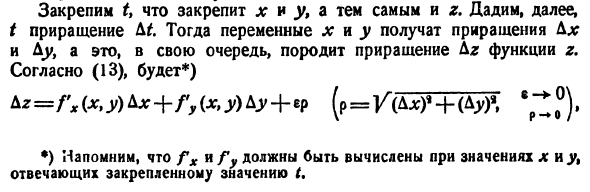
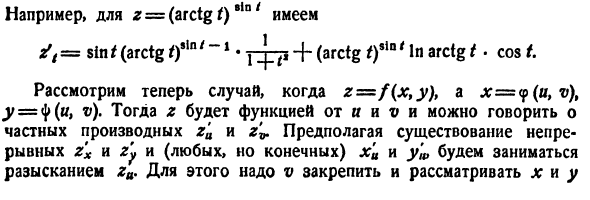
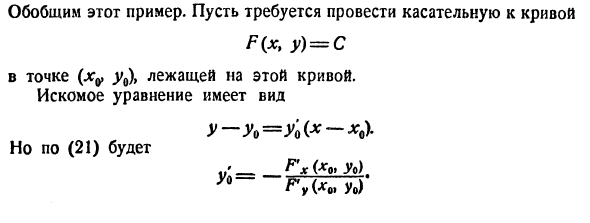
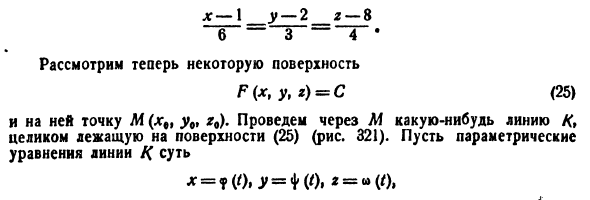
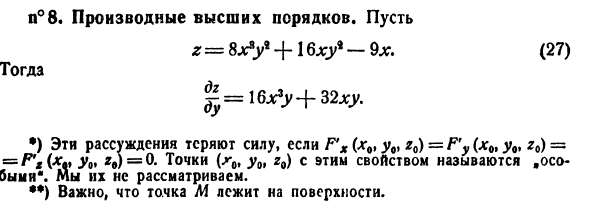
Производные функции нескольких переменных

• Производные функции для некоторых переменных № 1. Основная концепция. Глава II, дано понятие функции некоторых переменных. Мы изучим их более подробно здесь. Напомним, что если каждая пара значений x и y соответствует определенному значению z, переменная z называется функцией аргументов x и y. Эта ситуация отмечена в одной из формул z = f (x, y), z = y (x, y), z-F (x, y), z = z (xt y) и т. д. Кроме того, символ f (a, b) указывает значение (постоянное!)

Функции f (xt y). Это соответствует системе со значением x = a> y = b. Символ f (x \ y, z) t F (x t y, zy ut v) t определяется аналогичным образом. Первые x, yt z, второй случай x, y, z и v служат независимыми переменными. Само собой разумеется, что выражения f (a, b> c), F (a, b, c, d, e) означают. Техника и наука предоставляют множество примеров функции нескольких переменных. Ваш II уже упоминает закон Ома. Вот еще два примера. 1) Абсолютная температура T, давление p и объем v абсолютной массы газа связаны уравнением Клапейрона. pv = RT, Где R постоянная Отсюда То есть v является функцией двух переменных p и T. 2)

Температура нагреваемого объекта может варьироваться от точки к точке в определенный момент времени t. так G = 0 (дг, у, 2),Однако, если (7) является действительным числом, произведение, описанное здесь, должно быть равно -J-1 вместо -1. Вот несколько примеров нахождения частных производных: 1) Z = xy, z’x = yx * ~ * t Zy = Xy \ nx 2) 2 = arctga Zi = 3arctg ^. -U • A r \ = 3arctg ^ fx 1 + у * X -LG -? V5 » 3) г; = £ г; == ф.

Обобщение понятия частной производной на случай функции любого числа переменных не требует объяснения. Мы ограничимся этим примером № 4. Полная пошаговая формула. Если вы измените пары значений x и y и дадите им приращение Ax и Du, функция получит приращение Az = / (4 4 bx, y + yy) — / (*, y),

Функция z = f (xt y) не только непрерывна, но и каждая точка (x, y) также имеет обе частные производные f’x (x, y \ fy (xt y), которые также являются непрерывными функциями [ Производная точка (x, y)]. Людмила Фирмаль

Это называется «полным приращением» (в отличие от «частичного * приращения». «Частичное * приращение» генерируется путем увеличения только одного из аргументов при изменении других аргументов) , D * = [/ (* + Dat, Y + AU) -PX, y + Ay)] + + \ f (x> y + h) -f (*, y) b (9) Каждое выражение в скобках представляет приращение функции z. Это уже считается функцией с одним аргументом. В первой круглой скобке второй аргумент содержит значение константы jf-4-Ду, а во второй круглой скобке x является фиксированным. применимый

Формула Лагранжа в формулу: f (x + Lx, y + Ay) -f (*, y + Ay) = fx (5, y + Du) A *, f (*> y — * — * y) -f (x> y) = M *> (10) Где 5 между x и ηAjc, а m \ между y и jr + Ay. 5 lj, 7j-> Y, если Ajc и Dy стремятся к нулю. Следовательно, D- * 0 (Для преемственности а / к) / i & J ‘+ Ay) fy (x> y) —

Однако переменные, которые имеют тенденцию быть ограниченными, равны пределу и добавляются неограниченно. так fy (X, Ji) = fy (xt jO + ft Здесь a и p стремятся быть равными нулю для Ah и Au. Сравнение (9), (10) и (11) A * = /; (JC, y) Реклама + +; (LH, y) Ay + a Ah + p Au. Положить в 1 год | ^ B | Я и П0Т0МУ a | = nA * + RAU | 0. Пара отношений Aje- * 0, Ay-►О эквивалентна отношению p- * 0. Итак, наконец (13) (14) A z = fc (x, y) Ax — \ — f’y (x> y) Ay -J-ep, далее Уравнение (13), которое учитывает уравнение (14), называется уравнением полного приращения функции. № б. Дифференцировать сложные функции.

• В предположении, что существуют непрерывные производные z’x и z’y и производные x \ и y \, где z = f (x, y . (А) (12) И DLG-F-B сделать Где e = -r предполагается. рт исправлен. Это изменяет x и y, тем самым способствуя t и Af увеличиваются. Затем переменная хны получает приращения Д * и Ду, что вызывает приращение Дг функции r. (13) Согласно L2 = Tx (x> Y) L * — {- Gu (x, y) Ly — {- *? (P = YG (D ^ + (D ^ •) Напомним, что fx и fy должны быть рассчитаны для значения хны, соответствующего фиксированному значению t.

Откуда L Допустим, M0. Тогда Ajc-> 0, Ду0, и результат е0. Кроме того, так Это доказывает существование и равенство / 1 (15) (16) (17) = Gf y) xft + /; (x, y) /,. Это выражение может быть записано в эквивалентном формате. * t = z’x •• //> dz_dz dx, dz dy dt dx ‘dt ■ «55» dt Выражение (16) является расширением «правила цепочки *».

В уравнении (17) расположение символов d и q интересно, так что производную функции одной переменной можно отличить от частной производной функции нескольких переменных. Пример. Дай мне z = x>, x = x (t) t y = y (t). Тогда z’jg = yx * ~%, y = xy \ nx, так / t = yxy ~ lxfi -f-Xy \ n X. /,.

Например, если r = (arctan t), n ‘ = sint (arctg tfn ‘»1 • -ppi + (arctg tfQ’ в arctg t.cos Рассмотрим случай, когда z = f (xty) t и x = <p (u, v), y = ty (u, v). r является функцией от u и v, и мы можем говорить о частных производных z’u и ri. Предполагая, что есть последовательные z’x и g’u и (необязательно, но конечные) x’a и y, мы будем искать это.

И как функция. Но тогда проблема суммируется в уже рассмотренных случаях. Следовательно, zu существует и согласно (16) #_ G * I I * 2nd = ‘Hy -f- Zyya. дециграмм Более интересно написать это выражение, используя обозначение ^ на самом деле, (18) принимает вид (19) Если вы забудете, что символ не является дробью, (19) «Сокращая * с помощью dx и dh9, вы можете запутаться, потому что получите» dg_dg .dg_ ^ dg di cto ‘du di * Конечно, это смешно. № 6. Дифференциация неявной функции.

Подумай об уравнении F (xty) = Q (20) Где C = const Это уравнение может быть решено в терминах y в общих терминах, поэтому мы определяем y как (неявную!) Функцию от x. Таким образом, вы можете говорить о производных Ul. Показано, как найти уравнение (20), не решая его, то есть не найти явное уравнение для y относительно x. Чтобы сделать это, представьте, что нашли это явное выражение y = f (x) и присвоили функцию / (*) вместо аргумента y в (20). Далее (20) становится тождеством *) относительно x.

Другими словами, в (20), если y не является независимой переменной и подразумевает интересную интересующую функцию f (x), обе части (20) представляют одинаковые (но только разные) функции x. Найти производную этой функции (как говорится «Различить полученную идентичность»). Оказалось, что справа. (18)

Видимо 0. Чтобы найти производную левой части, рассмотрим, что левая часть (представленная z) является комплексной функцией от x z = F (x, y), y = f (x). Следовательно, формула (15) z’x = Fx (x> Y) x’x + Fy (x, Y) x’x = > и производная левой стороны (20) z’x найденного тождества должна быть равна 0 (то есть производной правой части), поэтому Fx (x, y) + F’y (x, y) yx = 0 Отсюда F ‘(y «l (21) Следует помнить, что x справа обозначает производную точку, а y является значением рассматриваемой неявной функции, соответствующей этому x. Пример. Рисовать на кривой xz + y * -2hu * = \ 7 (22) Касательная в точке (1, 2).

Невозможно найти явное задание для кривой. Однако легко убедиться, что точки (1, 2) находятся на этой кривой. Следовательно, значение x = 1 соответствует значению y = 2. Это может решить эту проблему. Другими словами, если левая часть (22) представлена ​​как F (x, y), F’x (x, y) = 5jc * -2y3, F [, (x, y) = 5y * -6hu \ So Г-5лг * -2у3Ух— И если jc = 1 (и y = 2) / = ~. Следовательно, касательная формула имеет вид:Подводя итог этому примеру: Я хочу нарисовать касательную к кривой F (xt y) = C Точка (xv y0 \ находится на этой кривой. Форма уравнения цели Y-Yaw = Yaw (x-Xo> — Но согласно (21) Fx (* o> V0) t V0 до G9 (x „y0)

Поэтому форма уравнения касательной имеет вид в Или то же самое n * 7. Плоскость, которая касается космической линии и касается поверхности. Изучить кривые, определяемые параметрическими уравнениями в пространстве * = 20) ~ «Точка кривой Т ° Й, соответствующая значению параметра t = t9. Найти уравнение касательной к прямой (23), построенное в точке М. Для этого Дает параметр с шагом At, обозначенным N (q: 0 -4- DG, y0 + Au, r% -Ag).

Точка, соответствующая значению t = t9-At, проходит через две заданные точки. Секущий MN как линия имеет каноническое уравнение. X-X0 __ U U o-g— * o Ах Ду Аг 9 Может быть написано в следующем формате X X0 ——— V —Y ”- * — * o & x Au Ay * В на О Ду Аг В случае 0 каждое из соотношений ^ связано = 2 ‘/ = «‘ (/ 0), поэтому форма целевого уравнения (24) Пример. Нарисуйте касательную линию x = z3t9-2, y = * »+! , R = 2 / v + 6 Точка * = 1. Решения. Где g0 = 1, y0 = 2, g0 = 8, г ‘, = 6 /, /, = 3 **, z’t = 4t, г * (1) = 6, y (1) = 3, z ‘(l) = 4 и искомая касательная v-v = & (x «Us) (x

То есть 0 является функцией трех аргументов x, y и z. Учитывая зависимость b от времени tt 0 = 0 (JC, y> Z, 0, То есть 6 является функцией четырех аргументов. Вы можете привести столько примеров, сколько захотите. Обычно несколько функций аргументов указываются с помощью явных методов анализа.

Например, это функции z = 2 * ‘+ 3y, u = X ^ t w = ex ^ B) Существует также неявное определение такой функции. Например, уравнение 3z-x-y-5 = 0 Неявно установить функцию х + у + 5 * ч • Систему значений (x, y) можно рассматривать как точку на плоскости. Следовательно, когда речь идет о функции z = f (x, y), часто говорят, что z является функцией точки (x, y). Чтобы определить функцию z = f (x, y), не только правило для нахождения z по заданным x и y, но также набор пар значений, которые могут принимать аргументы x и y (область функции и Также необходимо указать).

Для явного аналитического определения функции этот набор определяется выражением, которое определяет саму функцию. Например, функция z = x9 — \ — 2y (1) Дано всем видам х и у. Следовательно, пара чисел (x, y) — это координаты любой точки на плоскости. В связи с этим говорят, что функция (1) определена по всей плоскости. В отличие от функций x- \ _ y-2_z-S 6 3 4 e Давайте рассмотрим поверхность F (xtytz) = C (25) И указать на него точку M (x% ty0, r9). Нарисуйте линию K, которая проходит через M и полностью на поверхности (25) (рис. 321). Параметрическое уравнение прямой К * =? ( «). J> = «K0. * =» (‘),

Кроме того, если t = t0, отсюда получается точка M. Поскольку каждая точка линии K находится на поверхности, значение параметра t равно 14 * (Ot * (0. «0) 1 = C. Но это отношение тождество т. Различить и найти его Gb b (0, ♦ (0. • (01 (t) + ry [? (О, ♦ (0> • (01V (0 +) m «(0)« ‘(o = o. Поместите f = f0 здесь. Это дает соотношение Γχ (χ »V0. * •> Co) + Gu A» * •> f A) + ^ A. * o) A) = 0- (26) Как показывает уравнение (24), вектор r с проекцией (* 0), <| / (/ „), <* ‘(/„) (при удалении от точки M) находится в точке M к линии K Это на нарисованной касательной. Представляя вектор n = Tx ‘{x0, y0, + R’u Y ”* 0) J + Rs (* .. y * * * o) L.

Этот вектор полностью определяется поверхностью (25) и точкой M и не зависит от выбора кривой K. Уравнение (26) iat = 0 Это означает, что вектор m перпендикулярен вектору n. Поэтому, когда вектор l перемещается от M, даже если прямая K (25) на поверхности проходит через точку Af, касательная к этой линии (в точке M) перпендикулярна l и t. е. Находится в плоскости через M и перпендикулярно вектору l *). Эта плоскость называется касательной плоскостью поверхности (25) в точке М.

Уравнение явно имеет форму yo>)) (x- * •) + PG (x: Y »go) (Y- * •) + pg (* УY0, *,) (<-0. Вектор n называется нормалью поверхности в точке M (25). Например, нарисуйте плоскость, которая касается поверхности в точке M (1, 1, 1) x $ y * — \ — xz — \ — z ~ 3 • *). Решения. Где F \ = Zl’y F’y = 2 xy, F’g = x + 1. Следовательно, 1 »1) = 4« F’y (1, Г, 1) = 2, F ‘(l / l, 1) = 2, и искомое уравнение равно 4 (> -1) + 2 (yT) + 2 (2-1) = rO, то есть 2l + y + r-4 = 0. Рисунок 321.

Кроме того, если t = t0, это дает точку М. Поскольку каждая точка линии K находится на поверхности, значение параметра t равно 14 * (Ot * (0. «0) 1 = C.) Однако это соотношение является тождеством m. Его Gb b (0, ♦ (0. • (01 (t) + ry [? (О, ♦ (0> • (01V (0 +)) m «(0)« ‘(o = o. Положите f = f0, где это соотношение) Γχ (χ »V0. * •> Co) + Gu A» * •> f A) + ^ A. * o) A) = 0- (26) Как показано в уравнении (24), проекция вектора r (* 0), <| / (/ „), <* ‘(/„) (если выходить из точки M) расположены на линии K из точки M. Это на нарисованной касательной и является вектором n = Tx ‘(x0, y0, + R’u Y ”* 0) J + Rs (* .. y * * * o) L. Этот вектор является полным T определяется поверхностью (25) и точкой M,

Это не зависит от выбора кривой K. Уравнение (26) iat = 0 Это означает, что вектор m перпендикулярен вектору n, так что точка Af на поверхности прямой K (25) И касательная этой линии (в точке M) перпендикулярна l и t, то есть в плоскости, проходящей через M и перпендикулярно вектору l *. Эта плоскость является касательной к плоскости плоскости в точке M (25 Форма уравнения явно yo>))) (x- * •) + PG (x: Y »go) (Y- * •) + pg (* YY0, *,) (<-0 Вектор n называется нормалью поверхности в точке M (25), например, x $ y * — \ — xz — \ — z, которая рисует плоскость, которая касается поверхности в точке M (1,1,1) ~ 3 * *). Решения. Где F \ = Zl’y F’y = 2 xy, F’g = x + 1. Следовательно, 1 «1) = 4» F’y (1, Г, 1) = 2, F ‘(л / л, 1) = 2, целевое уравнение равно 4 (> -1) + 2 (yT) + 2 (2-1) = rO, то есть 2l + y + r-4 = 0. Рисунок 321.

DZ Я обнаружил, что сама производная ^ является функцией от x и y *). Поэтому его можно снова отличить по каждой переменной. Результатом производной по х является Результат дифференцирования по и относительно у дорога 3 * ^ 48 ^ + 32 «г = 16 *» + 32 *.

Обе эти функции называются частными производными второго порядка от z. Излишне говорить о значении символов д’дудхду * W То есть это результат последовательного дифференцирования в 5 раз по zt, первое дифференцирование выполняется по x, результат снова дифференцируется по x, новый результат выполняется по y, что делается по x и, наконец, Последняя производная сделана по y.

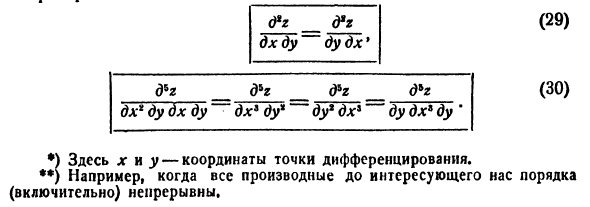
Применительно к функции (27) dg = 24dg + 16y-9, ~ = 4 8x д’г д * з дх * 1 ^ ‘дх9 Сделать Таким образом, дх * до дх до Чтобы получить производную (28) (которая является пятой производной), нам нужно дифференцировать функцию z 3 раза по x и 2 раза по y и выполнить эти дифференцирования в установленном порядке: сначала по x Дважды, затем y, затем x и, наконец, y. В большинстве случаев вы действительно встретите **), вы можете изменить порядок дифференцирования для отдельных аргументов.

Например d * z <Pr дх ду дух * d * z _ d * g _ dbz _ d * z dx1 du dx du dx * du * du * dx8 du d * 3 dy * (30) •) где x и y — координаты дифференциальной точки. • *) Например, если все производные (включая все) являются непрерывными до интересующего нас порядка.

Для функции (27) уже Я *? ^ -48хгу + 32_й. о Также оттуда = 48 ^ + 32 ,, (29) оказалось правдой. Читателю рекомендуется использовать тот же пример, чтобы проверить соотношение (30), и использовать независимо придуманный пример, чтобы проверить достоверность равенства. d’g__ d’g du dh> du dh1 dl * du * ‘ Все, что можно сказать, легко переносится на любое количество функций аргументов. Например, h = f (*, y, z \ Затем вы можете ввести производные формы дг> и дх до * дг дх Такие, как. Опять же, порядок индивидуальной дифференциации безразличен.

Дано только (интересует только фактическое значение z), т.е. обведено (включая контуры!) Круг jc9 -} — j / 9 = 1. функция Установлены на тот же круг, но больше не содержат точек контура. функция z = Vx — у x ^ y eadana, то есть правая сторона линии x = y.

Точно так же понятие области задач вводится в функцию любого числа переменных. Функция двух переменных позволяет иллюстрации. То есть функция z = f (x, y \ graph j), заданная несколькими наборами S S точек на плоскости xy, в простейшем случае такой граф представляет конкретную поверхность.

Функция трех (и более) переменных не имеет геометрического представления. Однако все наиболее важные факты из теории функций многих переменных уже были обнаружены с функцией f (xt y)>, и мы в основном изучаем их. № 2. Преемственность. Понятие непрерывности функции для нескольких переменных определяется так же, как функции для одной переменной. Пусть z = f (x, y). Дайте x и y} на основе приращения bx, ay значение x = x # y = yp. Это генерирует приращение Az функции z = f (x, y).

* Если (2) (3) lim Az = 0, Ax-f A.u— • Другими словами, бесконечное приращение аргумента соответствует бесконечному приращению функции, и функция называется непрерывной [начальное значение аргумента x = x # y = yv или, короче, точка (xv d ^]). A * = /(.* E-f A *, L + Au) -f (x \ И положить = yQ — \ — by =: Если yt, отношение (2) можно переписать как __ lim f (x, y) = f (x * y0). y ~ y «

Таким образом, непрерывность функции означает, что предел равен значению из предела аргумента. Функции являются непрерывными в некоторых отношениях и не непрерывными в других. Так, например, функция / (*. ‘(4) *) Обратите внимание, что парное отношение ддг- * 0, у вас * 0 эквивалентно одному отношению (ддг) «» (AU) » + Uv + Doo) до * Point (* 01 Wo).

Он непрерывен по всей плоскости, кроме точки (0, 0). На этом последнем этапе ни одна функция не определена. Однако даже если задача функции (4) установлена ​​в точку (0, 0) и пополнена, форму уравнения / (0, 0) = A На этом этапе непрерывность не может быть достигнута. И mf (x, y) = -f-oo, А всегда означает конечное число. Определение непрерывности функции трех или более аргументов ничем не отличается от того, что рассматривается. № 3.

Частные деривативы. Пусть z = f (xt y). Измените точку (jcq, y0) и дайте аргументу x приращение Ax без изменения фиксированного значения аргумента y = y. Ограничение *) lim f + y0) ~~ f (l? 0 ‘Al-0 Называется частной производной функции f (x, y) в точке (Xq, yo) по аргументу x и обозначается одним из символов. / * {**> Y *)> (5) Нахождение производной z’x называется производной функции z по аргументу q, а точка (q, y0) называется производной точкой. Остальное несколько неполно, как показано только в первой записи (5). Частная производная по y определяется аналогично. Do — 0 U

Таким образом, частная производная функции по одному из двух ее аргументов является наиболее распространенной производной функции одной переменной и берется из функции при изменении другого аргумента. Например, z = 3xY — \ — x + y (6) Найдите z’x в точке (5, 2). Для этого измените значение y = 2 и преобразуйте z в одну функцию x. z = 24dg9 + lg + 2. *) Может не существовать Производная этой функции в любой точке x имеет вид *; = 48jc + 1 В точке * = 5 zx = 241. Это решение проблемы. В общем, они предпочитают находить zx и z’y, оставляя буквенное обозначение (x, y) в точке различия.

Таким образом, для функции (6), предполагая, что x является переменной, а y является константой, 1. Как хорошо В частности, взяв * = 5 и .y = 2 zx = 241, zy = 901. Обратите внимание на одну особенность обозначения. J т Обратите внимание, что это фиксированный символ z’xt, а не дробь *). Если вы забудете об этом, может произойти ошибка. Пример. Ассоциируйте переменные x, y и z следующим образом: hoog = . (8) В этом случае каждая из этих переменных является двумя другими функциями.

Явное назначение этих функций выглядит следующим образом: hu * y g ‘y zx’ Отсюда dz _ —1 dx_zzL — 1 d * • ** >> ‘d ^ yz’ dz g * x * Умножение этих равенств дает dz dx ^ f> _-1 d * ‘dy dz (xyz) a dg dx do _ f *) Отличается от обозначения производной функции, чем (7) Один аргумент z = f (x). Конечно, в конце концов, есть ~ Реальное число Обратите внимание, что символы qx и qx сами по себе не имеют смысла (в отличие от dx и dz). Благодаря (8)

Смотрите также:

Предмет высшая математика

Поверхности 2-го порядка	Экстремальные значения функции нескольких переменных
Преобразование координат	Полный дифференциал