Оглавление:

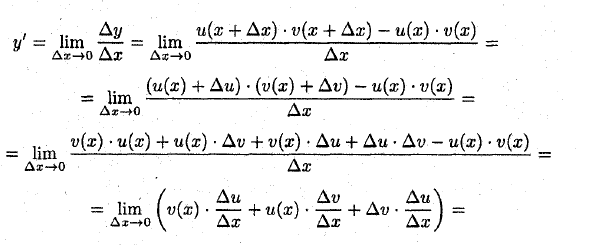


Производная суммы, разности, произведения и частного функций
- Производные, различия, продукты и частные характеристики Нахождение производных функций непосредственно по определению часто связано с конкретными трудностями. На практике функции дифференцируются с использованием нескольких правил и выражений. Пусть u = u (x) и v = v (x) две дифференцируемые функции на определенных интервалах (a; b).
Теорема 1.По определению производной и основной предельной теореме получаем , ^ J {и (x + Ax) ± v (x + As)) — ± y (x)) -lim (+ -μ (x) ± v (x + «*» v (x) ^ _ d * — + o \ Да; топор J Ай Ав, = lim ± Urn- = и ± v, Dg-> o Dy Dx to »o Da; То есть (u ± y) ‘= u’ ± v ‘. % It- Теорема верна для конечного числа членов. Теорема 2. Производная произведения двух функций равна произведению производных первого и второго факторов и первого и второго факторов: (uy) ‘= u’-y + y ‘• ты. 4 Пусть у = уу. тогда
Производная суммы (разности) двух функций равна сумме (разности) производных этих функций: (u ± y) ‘= и’ ± y ‘. • 4 обозначает y = и ± y. Людмила Фирмаль
‘-lim-lim + ^^ + ^^ — t / (a?) • r> (x) D1-40 Dx Dx- + o Dx т. (U (x) + Au) • (v (x) + Av) -u (x) • v (x) = urn- Дх ~ * 0 дх v (x) • u (x) -f u (x) • Av + v (x) • Au + Di • Av-u (x) • v (x) ободок Dh -lim (v (x) • ^ + u (x) • ^ -Av • ^ | = Dx- * o \ Dx Dx Ax J / 4 1. / 4 1. 1-l v = v [x) • lim — Mix xlim — f-lim Av • lim- = Dh-ю топор Dh — топор Dh-ю Dh—> о топор = u » V -f и -v ‘+ 0 • Это’ = v! • V + и • V \ То есть (u • v) ‘= v! • v 4- и -v ‘. ■ ‘► Для доказательства теоремы мы использовали теорему о связи между непрерывностью и дифференцируемостью.
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Функции u = • u (z) и v = v (x) непрерывны, потому что они дифференцируемы. Следовательно, Av-> 0 и Au-> 0 могут быть показаны как Ax- »0 или менее. a) (c • u) ‘= c • и \ где c = const; б) (u-v-w) ‘= u’ • V-w + и • r / • w + wv-w ‘. Теорема 3. Дифференцирование фактора двух функций j ^ j v (x) φ0 равно дроби, которая является разностью между произведением дробного знаменателя и производной числителя и дробным числителем, числителем знаменателя и производной знаменателя, где знаменатель равен (\ I I / = — ‘V ~ £ U’V} Vj £ 0. <
Тогда , __] im vg + gg vgj = дх-> о топор -lim ~~ ‘^ V Топор Dx-40 • (v (x) + Av) v (x) Вау-БЛА = hm —— 5-— = lim- ^ ——— Дх-и) Дя • (tr-L v • Dee) -Дх—> o vz + v • Дг> ти. lim lim | A 、 DhchO Dh— »0 U V т? 2 + V • Lim D? ; 1 Dx- ^ o е. (M) = уф-уф (И результат \ ‘1 1. J = j • u’. (C \ f 1 -) = -, где с является конст. VJ V
Пусть Y ~ Людмила Фирмаль

