Оглавление:
Производная сложной и обратной функций
Пусть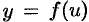 
и 
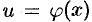, тогда 
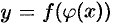— сложная функция с промежуточным аргументом и и независимым аргументом 
.
Теорема 20.5. Если функция 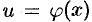имеет производную 
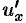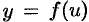в точке , а функция имеет производную 
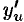в соответствующей точке 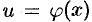, то сложная функция 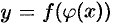имеет производную 
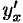в точке , которая находится по формуле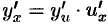 
.
По условию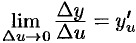 
. Отсюда, по теореме о связи функции, ее предела и бесконечно малой функции, имеем 
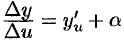или
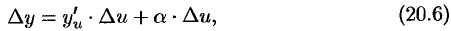
где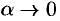 
при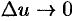 
.
Функция 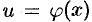имеет производную в точке 
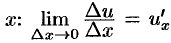, поэтому
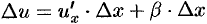, где 
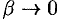при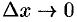 
.
Подставив значение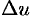 
в равенство (20.6), получим
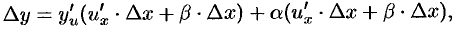
т.е.
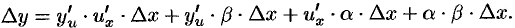
Разделив полученное равенство на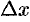 
и перейдя к пределу при 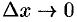, получим .
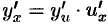Итак, для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.
Это правило остается в силе, если промежуточных аргументов несколько. Так, если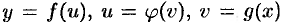 
, то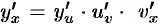 
. Пусть 
и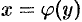 
— взаимно обратные функции.
Теорема 20.6. Если функция строго монотонна на интервале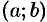 
и имеет неравную нулю производную 
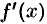в произвольной точке этого интервала, то обратная ей функция 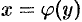также имеет производную 
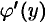в соответствующей точке, определяемую равенством 
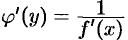или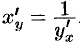 
.
Рассмотрим обратную функцию 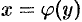. Дадим аргументу 
приращение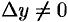 
. Ему соответствует приращение 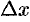обратной функции, причем 
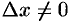в силу строгой монотонности функции . Поэтому можно записать
Если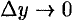 
, то в силу непрерывности обратной функции приращение 
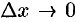. И так как 
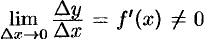, то из (20.7) следуют равенства 
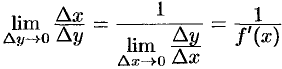, т.е. 
.
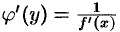Таким образом, производная обратной функции равна обратной величине производной данной функции.
Правило дифференцирования обратной функции записывают так:
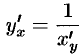или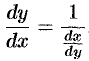 
.
Пример №20.3.
Найти производную функции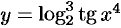 
.
Решение:
Данная функция является сложной. Ее можно представить в виде цепочки «простых» функций: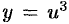 
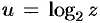, где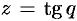 
, где 
, где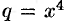 
. По правилу дифференцирования сложной функции 
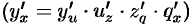получаем:
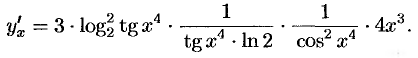
Дополнительный пример №20-4.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
