Производная сложной и обратной функций

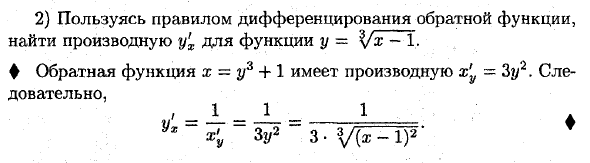
Производная сложной и обратной функций

• Комплексная и обратная производная функция Если y = f (u) и u = ip (x), y = f (0 д Q ^ = y’h + a или его предел и бесконечная функция D | / = 2 / J4 • Au + a- Au, (1) Где-> 0 и Di —► 0. Функция w = ip (x) имеет производную в точке x: lim ^^ = y’x, таким образом Au = u’x Ax + (3 Ax, где / 3-> ■ 0 — Dx-> 0. Подстановка значения Di в уравнение (1) дает Ду = • Да. + P • Lx) + • Lx + 0Lx), Это Du = y’i • u, • Dx + y’i • /? • Dx 4-h’x • a • D x + a-fi Ax. Разделив полученное равенство на Dx и достигнув предела как Ax-0, получим y’x-y’u-uh. ►

Это правило остается в силе, если есть несколько промежуточных аргументов. Следовательно, y = f (m), а -y? (R>), v = ^ (… m), y’x = y’u-u’v ■ v’x. y = f (x) и x = ip (y) являются обратными функциями друг от друга.

Следовательно, чтобы найти производную комплексной функции, производная этой функции по промежуточной функции должна быть умножена на производную по промежуточной функции.му аргумент. Людмила Фирмаль

Теорема 2. Если функция y = f (x) строго монотонна на интервале (a; b) и имеет ненулевую производную f ‘(x) в любой точке этого интервала, функция x = <p ( y) также является точкой, соответствующей производной <p ‘(y), уравнению tp’ (y) = ym ^ y или x’y =

• Решение задач по высшей математике

Связь между непрерывностью и дифференцируемостью функции	Производные основных элементарных функций
Производная суммы, разности, произведения и частного функций	Гиперболические функции и их производные

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

• Рассмотрим обратную функцию M x = дать аргумент y Инкремент Ay0. Это соответствует обратному приращению Ax, и Ax> 0 из-за строгой монотонности функции y = f (x). Так что вы можете написать ^ = J- (2) В случае Au 0, увеличение Ax-> 0 из-за непрерывности обратной функции. (Lim-fix) Φ0, так (2) Уравнение Ш ^^^ == ^ т.е. , где z = tgq, q = x4.

2) Найти производную y’x функции y = Yx-1, используя правила дифференцирования обратной функции. ♦ обратная функция x = y + 1 производная = 3? D Поэтому , J_ J_ _ 1 г * » 32/2 3.

Правила дифференцирования комплексных функций (y’x = Y и • u’z • zq ‘q’z) дают: у’х = 3 • log * tg * 4 • —2—— ■ -4-4 ‘4x * • ♦ tg x * • В 2 cos X4 Людмила Фирмаль