Оглавление:
Производная сложной функции
Теорема 5.3. Если функция 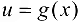 дифференцируема в точке
дифференцируема в точке 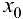 , а функция
, а функция 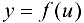 дифференцируема в точке
дифференцируема в точке 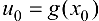 , то сложная функция
, то сложная функция 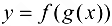 дифференцируема в точке
дифференцируема в точке 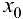 и
и
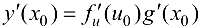
Доказательство.
Так как функция 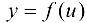 дифференцируема в точке
дифференцируема в точке 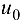 , то приращение этой функции в точке
, то приращение этой функции в точке 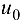 может быть записано в виде
может быть записано в виде
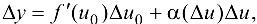
где 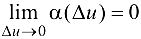 . Разделим равенство (5.5) на
. Разделим равенство (5.5) на 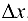 . получим
. получим
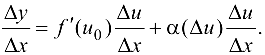
Равенство (5.6) справедливо для любых достаточно малых 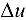 . Возьмем
. Возьмем 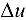 равным приращению функции
равным приращению функции 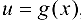 , соответствующему приращению
, соответствующему приращению 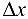 аргумента
аргумента 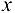 в точке
в точке 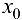 , и устремим в этом равенстве
, и устремим в этом равенстве 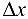 к нулю. Так как по условию функция
к нулю. Так как по условию функция 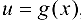 имеет в точке
имеет в точке 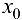 производную, то она непрерывна в этой точке. Следовательно, согласно определению непрерывности,
производную, то она непрерывна в этой точке. Следовательно, согласно определению непрерывности, 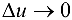 при
при 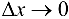 . Но тогда и
. Но тогда и 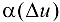 также стремится к нулю, т. е. имеем
также стремится к нулю, т. е. имеем
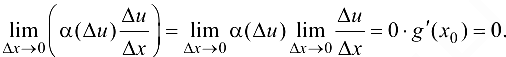
В силу соотношения (5.7) существует предел правой части равенства (5.6) при 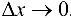 , равный
, равный 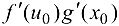 . Значит, существует предел при
. Значит, существует предел при 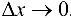 и левой части равенства (5.6), который, по определению производной, равен производной сложной функции
и левой части равенства (5.6), который, по определению производной, равен производной сложной функции 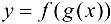 в точке
в точке 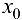 . Тем самым доказана дифференцируемость сложной функции и установлена формула (5.4). ■
. Тем самым доказана дифференцируемость сложной функции и установлена формула (5.4). ■
Замечание 5.2. Формула (5.4) может быть усложнена. Например, если 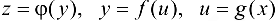 и все три функции имеют производные в соответствующих точках, то
и все три функции имеют производные в соответствующих точках, то
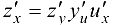
Пример 5.6.
Найти производную функции 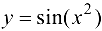 .
.
Решение:
Данную функцию можно представить в виде 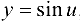 , где
, где 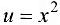 . Тогда, по формуле (5.4), получаем
. Тогда, по формуле (5.4), получаем
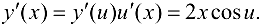
Заменяя на 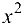 , окончательно получим
, окончательно получим 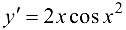 .
.
Ответ: 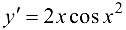 .
.
Пример 5.7.
Найти производную функции 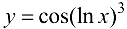 .
.
Решение:
Данную функцию можно представить в виде 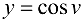 , где
, где 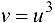 а
а 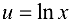 . Используя формулу (5.8), получаем
. Используя формулу (5.8), получаем
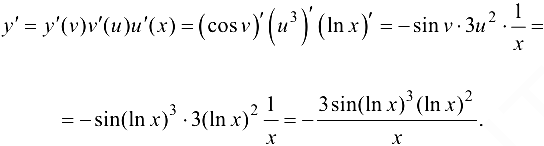
Ответ: 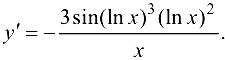
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:

