Оглавление:
Производная сложной функции. Полная производная
Пусть  — функция двух переменных
— функция двух переменных  и
и  , каждая из которых является функцией независимой переменной
, каждая из которых является функцией независимой переменной  :
: 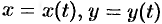 . В этом случае функция
. В этом случае функция 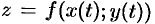 является сложной функцией одной независимой переменной
является сложной функцией одной независимой переменной  ; переменные
; переменные  и
и  — промежуточные переменные.
— промежуточные переменные.
Теорема 44.4. Если  — дифференцируемая в точке
— дифференцируемая в точке 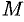
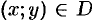 функция и
функция и 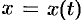 и
и 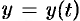 — дифференцируемые функции независимой переменной
— дифференцируемые функции независимой переменной  , то производная сложной функции
, то производная сложной функции 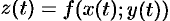 вычисляется по формуле
вычисляется по формуле
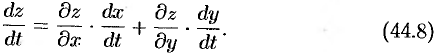
Дадим независимой переменной  приращение
приращение 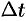 . Тогда функции
. Тогда функции 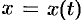 и
и 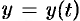 получат приращения
получат приращения 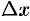 и
и 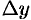 соответственно. Они, в свою очередь, вызовут приращение
соответственно. Они, в свою очередь, вызовут приращение 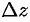 функции
функции  .
.
Так как по условию функция  дифференцируема в точке
дифференцируема в точке 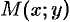 , то ее полное приращение можно представить в виде
, то ее полное приращение можно представить в виде
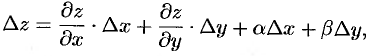
где 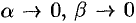 при
при 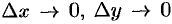 (см. п. 44.3). Разделим выражение
(см. п. 44.3). Разделим выражение 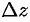 на
на 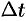 и перейдем к пределу при
и перейдем к пределу при 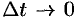 . Тогда
. Тогда 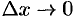 и
и 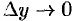 в силу непрерывности функций
в силу непрерывности функций 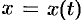 и
и 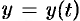 (по условию теоремы — они дифференцируемые). Получаем:
(по условию теоремы — они дифференцируемые). Получаем:
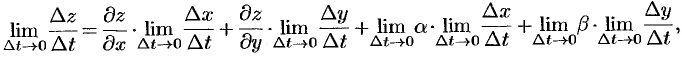
т.е.
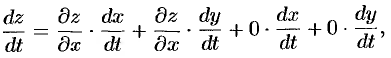
или
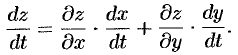
Частный случай:  , где
, где 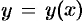 , т. e.
, т. e. 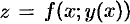 — сложная функция одной независимой переменной
— сложная функция одной независимой переменной  . Этот случай сводится к предыдущему, причем роль переменной
. Этот случай сводится к предыдущему, причем роль переменной  играет
играет  . Согласно формуле (44.8) имеем:
. Согласно формуле (44.8) имеем:
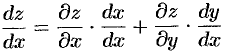 или
или 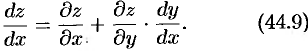
Формула (44.9) носит название формулы полной производной.
Общий случай:  , где
, где 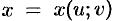 ,
, 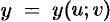 . Тогда
. Тогда 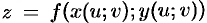 — сложная функция независимых переменных
— сложная функция независимых переменных 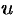 и
и 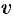 . Ее частные производные
. Ее частные производные 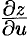 и
и 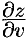 можно найти, используя формулу (44.8) следующим образом. Зафиксировав
можно найти, используя формулу (44.8) следующим образом. Зафиксировав 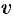 , заменяем в ней
, заменяем в ней 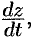
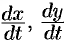 соответствующими частными производными
соответствующими частными производными 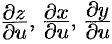 .
.
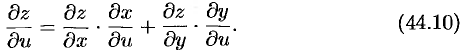
Аналогично получаем: 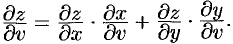
Таким образом, производная сложной функции ( ) по каждой независимой переменной (
) по каждой независимой переменной (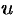 и
и 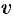 ) равна сумме произведений частных производных этой функции (
) равна сумме произведений частных производных этой функции ( ) по ее промежуточным переменным (
) по ее промежуточным переменным ( и
и  ) на их производные по соответствующей независимой переменной (
) на их производные по соответствующей независимой переменной (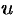 и
и 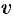 ).
).
Пример №44.5.
Найти 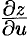 и
и 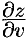 , если
, если 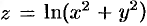 ,
, 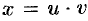 ,
, 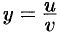 .
.
Решение:
Найдем 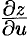 (
(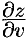 — самостоятельно), используя формулу (44.10):
— самостоятельно), используя формулу (44.10):
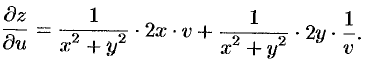
Упростим правую часть полученного равенства:
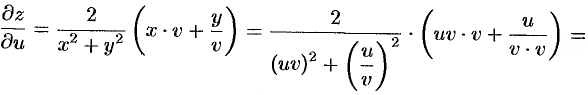
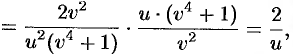
т.е. 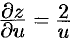 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Применение полного дифференциала к приближенным вычислениям |
| Дифференциалы высших порядков |
| Инвариантность формы полного дифференциала |
| Дифференцирование неявной функции |

